Построение плана положений и планов скоростей механизма. Построение графика, приведённого к ведущему звену момента инерции механизма

3.1.2 Построение плана положений и планов скоростей механизма.

Отрезок, изображающий на чертеже длину кривошипа ОА принимаем равным 50 мм.

(1)

Определяем масштабный коэффициент для построения планов положений:

(2)

Определяем длинны звеньев на чертеже с учётом масштабных коэффициентов:

(3)

Так как  l_AS2=l _CS4=l _AB/3, то

 

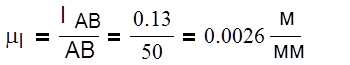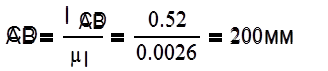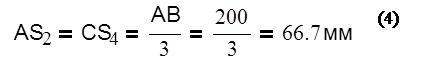Методом засечек строим двенадцать планов положений механизмов, приняв за нулевое такое положение, когда все звенья механизма выстроены в одну линию.

(5)

Линейная скорость точки С

V_C=ω₁l_ОС;

(6))

где ω₁  - угловая скорость ведущего звена; l_ОС – длина звена ОС, м.

(7)

где n₁  - частота вращения звена АС, об/мин.

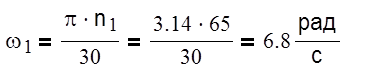V_C=6,8*0,13=0,88 м/с.

(8)

Скорость точки С изобразим в виде вектора pc, длину которого примем 50 мм. Тогда масштабный коэффициент для построения плана скоростей:

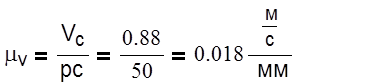Скорость точки D определим из следующих векторных уравнений:

(9)

V_D=V_C+V_CD;

V_D┴OD.

Также можем составить аналогичную систему уравнению для  определения скорости V_B:

(10)

V_B=V_B+V_BA;

V_B┴OB.

Численную величину абсолютной и относительной скоростей любой точки механизма определяется умножением соответствующего вектора скорости, взятого из плана скоростей, на масштабный коэффициент.

Из плана скоростей для первого положения:

V_S2=PS₂*μ_v=38*0,018=0,684 м/с;

V_b=Pb*μ_v=20*0,018=0,36 м/с;

V_ab=ab*μ_v=45*0,018=0,81 м/с;

V_S4=PS₄*μ_v=40*0,018=0,72 м/с;

V_d=Pd*μ_v=30*0,018=0,54 м/с;

V_cd=cd*μ_v=45*0,018=0,81 м/с.

Результаты расчётов для всех двенадцати положений занесём в таблицу 2.

Таблица 2 – Определение скоростей точек механизма.

№ поло-жения	Скорости точек, м/с.
	Vа		VS2		Vb		Vab		Vc		VS4		Vd	Vcd
0	0,9	0,63		0		0,9		0,9		0,63		0		0,9
1	0,9	0,684		0,36		0,81		0,9		0,72		0,54		0,81
2	0,9	0,81		0,684		0,45		0,9		0,864		0,846		0,45
3	0,9	0,9		0,9		0		0,9		0,9		0,9		0
4	0,9	0,864		0,864		0,45		0,9		0,81		0,684		0,45
5	0,9	0,684		0,54		0,81		0,9		0,684		0,36		0,81
6	0,9	0,63		0		0,9		0,9		0,63		0		0,9
7	0,9	0,684		0,54		0,81		0,9		0,684		0,36		0,81
8	0,9	0,864		0,864		0,45		0,9		0,81		0,684		0,45
9	0,9	0,9		0,9		0		0,9		0,9		0,9		0
10	0,9	0,81		0,684		0,45		0,9		0,864		0,846		0,45
11	0,9	0,684		0,36		0,81		0,9		0,72		0,54		0,81
12	0,9	0,63		0		0,9		0,9		0,63		0		0,9

Определим угловые скорости звеньев:

ω₁=6,8 рад/с; ω_2i=V_abi/AB; ω_4i=V_CDi/CD; ω₃=0; ω₅=0.

Вычислим угловые скорости звеньев 2 и 4 для двенадцати положений и полученные данные занесём в таблицу 3.

Таблица 3 – Определение угловых скоростей механизма.

Пол-е	0	1	2	3	4	5	6	7	8	9	10	11	12
ω2	1,7	1,6	0,9	0	0,9	1,6	1,7	1,6	0,9	0	0,9	1,6	1,7
ω4	1,7	1,6	0,9	0	0,9	1,6	1,7	1,6	0,9	0	0,9	1,6	1,7

3.1.3 Построение графика приведённого к ведущему звену момента инерции механизма.

Определим приведённый к ведущему звену момент инерции механизма в зависимости от угла поворота по формуле:

(11))

где, J_дв – момент инерции движущих сил, J_si – момент инерции звеньев, m_i – массы звеньев, V_i – линейные скорости звеньев, ω_i – угловые скорости звеньев.

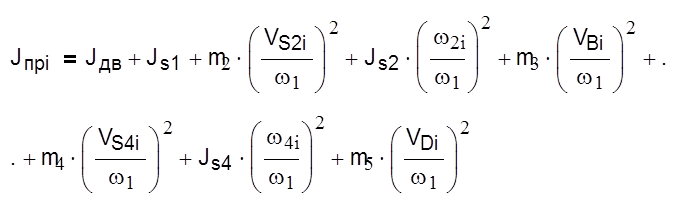Рассчитаем момент инерции для первого положения:

Вычисленные значения J_пр запишем в таблице 4:

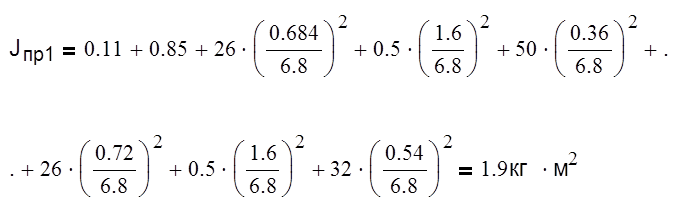Таблица 4 – Определение приведённых моментов инерции механизма.

Пол-е	0	1	2	3	4	5	6	7	8	9	10	11	12
Jпркгм2	1,5	1,9	2,8	3,3	2,9	1,9	1,5	1,9	2,9	3,3	2,8	1,9	1,5

(12))

Для построения графика приведённых моментов инерции примем, что длинна отрезка l_Jпр1=38мм.Тогда масштабный коэффициент при построении графика приведённых моментов инерции будет равен:

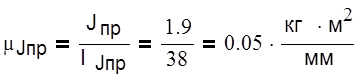По полученным данным построим  график приведённых моментов инерции механизма.

3.1.4 Построение графика моментов сил сопротивления и движущих сил.

Для определения моментов сил сопротивления определим приведённую силу, приложенную к ведущему звену.

На повёрнутых планах скоростей к центрам тяжестей звеньев приложим силы тяжести G_B, G_D, G₂ и G₄, к точкам В и D силы, действующие на поршни, к точке А, перпендикулярно звену АС приведённую силу, которую направим против движению ведущего звена.

Силы тяжести каждого звена механизма определим по формуле:

G_i=m_ig,                         (13)

где m_i- масса i-ro звена, кг; g - ускорение свободного падения, g = 9,81 м\с.

Тогда силы тяжести для звеньев будут равны:

G_В=m₃g=50*9,81=490 Н.

G_D=m₅g=32*9,81=313,6 Н.

G_S2= G_S4=m_S2g=26*9,81=254,8 Н

Для определения сил сопротивления строятся индикаторные диаграммы, по которым определяется давление в цилиндрах. Для построения диаграммы используем значения из таблицы 5.

Таблица 5 - Зависимость давления воздуха от перемещения поршня.

Относительное перемещение поршня		0,0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Давление в цилиндре	1 ступень, вверх Р1/Р1max движение вниз	1,00 1,00	1,00 0,30	1,00 0,00	0,55 0,00	0,38 0,00	0,27 0,00	0,18 0,00	0,12 0,00	0,08 0,00	0,04 0,00	0,00 0,00
	2 ступень, вверх Р2/Р2max движение вниз	1.00 1.00	1.00 0.54	1.00 0.30	0.70 0.30	0.59 0.30	0.50 0.30	0.42 0.30	0.37 0.30	0.34 0.30	0.32 0.30	0.30 0.30

(14))

P_1max=0,25 МПа. Примем за P_1max отрезок l_P1max=70 мм. Тогда масштабный коэффициент будет равен:

Из полученной индикаторной диаграммы определим все 12 значений P₁ и P₂. Зная диаметры цилиндров, определим силы сопротивления.

F_c=p*S,                           (15)

где S – площадь поршня, p – давление в цилиндре.

S=πd²/4;                          (16)

Для первого положения:

F_СВ=0,0054*10⁶*0,107=577,8 Н;

F_СD=0,468*10⁶*0,035=16380 Н.

Полученные значения сил сопротивления и давлений в цилиндрах занесём в таблицу 6:

Таблица 6 – Значения сил сопротивления.

Пол-е	0	1	2	3	4	5	6	7	8	9	10	11	12
РВ, МПа	0	0,005	0,022	0,051	0,151	0,25	0,25	0,094	0	0	0	0	0
РD, МПа	0,84	0,468	0,25	0,25	0,25	0,25	0,25	0,26	0,288	0,36	0,673	0,84	0,84
FСВ, Н	0	577,8	2311	5478	16178	26750	26750	10015	0	0	0	0	0
FСD, Н	29400	16380	8750	8750	8750	8750	8750	9100	10080	12600	23555	29400	29400

(17)

После чего, расставляем силы на повёрнутом плане скоростей и из выражения:

Находим приведённую силу. Для первого положения:

F_СВ*30+G_D*30-G_S2*27+G_S4*24+G_В*20+F_СD*20-F_пр*50=0

Подставив численные значения, получим: F_пр=6891 Н.

Приведенный момент будет равен: М_пр=F_пр*l_ОА=6891*0,13=895