Определение высоты поднятия ртути в дифманометре и высота поднятия воды в закрытом пьезометре

Задача №1.

В закрытом резервуаре налита вода. Определить высоту h поднятия ртути в дифманометре и высоту h₂ поднятия воды в закрытом пьезометре, если показание пружинного манометра, подключенного на уровне точки А, равно р_м = 180 кПа (0,17 МПа) (рисунок 1). Атмосферное давление р_ат считать нормальным, глубина погружения точки А равна h₁ = 7 м.                     

Плотность  ртути ρ = 13600 кг/м³,  воды ρ =1000 кг/м³.

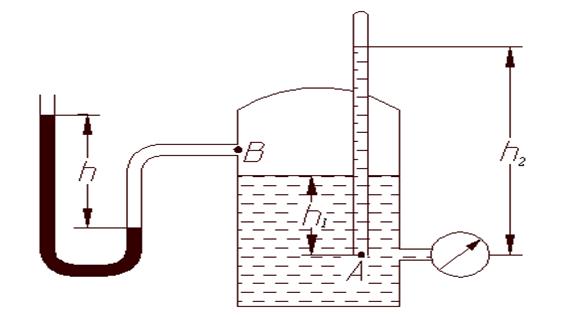
Рисунок 1

Решение:

Для решения данной задачи воспользуемся основным уравнением гидростатики р = р₀ + ρgh = р₀ + hγ,                                                           (1)

где            р₀  – давление, приложенное к поверхности жидкости, Па  ;

γ – удельный вес жидкости,  Н/м³.

При помощи уравнения (1) можно определить давление в любой точке покоящейся жидкости. Это давление, складывается из двух величин: давления р₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности жидкости р₀.

Согласно закону Паскаля давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Обозначаем на чертеже линии равного давления. Определяем поверхность с известным давлением, находим давление на следующей поверхности, применяя уравнение (1). Решаем уравнение относительно искомого параметра.

Вычислим величину давления жидкости и в точке В:

 

Высота столба жидкости в пьезометре поднимается на высоту h₂, пропорционально величине давления Р_м в точке А:

, следовательно, высота жидкости:

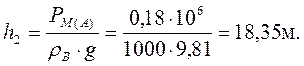
Найдем высоту h, на которую поднимается ртуть в дифманометре, записав условие равновесия относительно точки С. В точке С действует давление Р_С=Р_В=Р₀, по закону Паскаля: в ограниченном пространстве давление передается всем точкам пространства по всем направлениям одинаково.

, отсюда следует

 

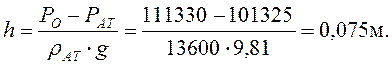
Ответ: h = 0,075 м, h₂ = 17,3 м.

Задача №2

В цилиндрическом сосуде диаметром  D₀ = 0,3 м  и высотой Н₀ = 0,5 м налита вода с начальным уровнем h = 0,3 м (рисунок 2) . Определить:

1.  Будет ли выплескиваться вода, если сосуд будет вращаться с постоянной частотой вращения n = 86 мин^-1?

2.  На каком расстоянии z₀ от дна будет находиться самая низшая точка свободной поверхности?

3.  С какой частотой нужно вращать сосуд, чтобы вода поднялась до краев сосуда?

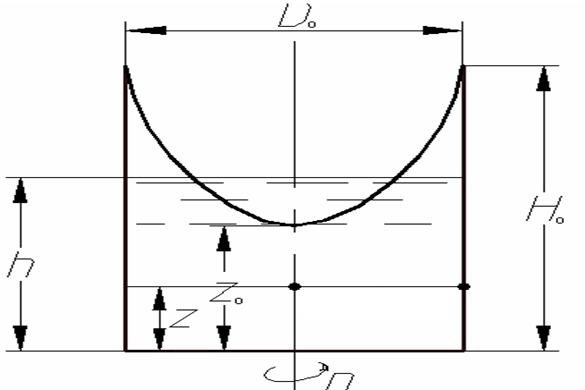
Рисунок 2

Решение:

Определяем n₂ и ω₂

Объем до вращения равен объему параболоида вращения

,

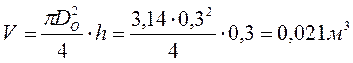Объем параболоида можно определить по формуле  где r – координата точки на свободной поверхности жидкости, соответствующая координате z, приравниваем две формулы

, отсюда Н равняется:

,

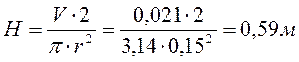Из чертежа видно: 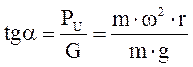, а также 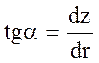, тогда 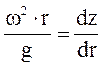, отсюда  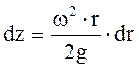проинтегрировав получаем .

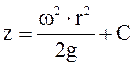Получаем уравнение свободной поверхности жидкости 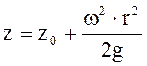, при n₂, z = H₀, z₀ =z^`₀, , тогда 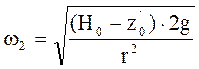 или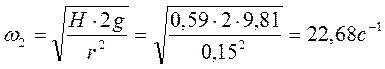  

 

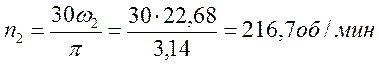
Найдем высоту от нижней точки параболоида до дна сосуда:

Найдем угловую скорость для первого условия:

Так как , то вода выплескиваться не будет, высота параболоида будет: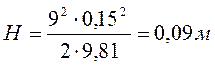

Задача №3

Треугольное отверстие AВС в вертикальной стенке закрытого резервуара, представляющее равносторонний треугольник, закрыто щитом (рисунок 3). Определить равнодействующую силу гидростатического давления бензина на щит и точку ее приложения, если заданы линейные размеры: h = 2,8 м, а = 1,6 м  и манометрическое давление р_м = 790 мм. рт.ст. (105070 Па) на свободной поверхности бензина.

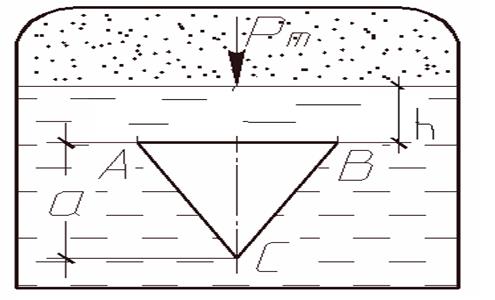
Рисунок 3

Решение:

Равнодействующая сила гидростатического давления бензина на щит составит:

Где – S – площадь щита, равное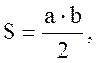

b – сторона равностороннего треугольника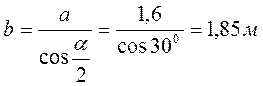

a – высота треугольника

,

h_ЦТ – высота от свободной поверхности бензина до центра тяжести щита:

,

.

Точка приложения равнодействующей силы гидростатического давления не будет совпадать с центром тяжести плоской поверхности щита. Эта точка находится на расстоянии от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки 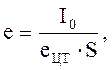 где е_цт = h_цт , I₀ – момент инерции площадки S относительно центральной оси

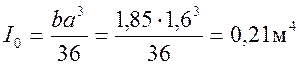
Найдем высоту расположения точки приложения усилия Р

 

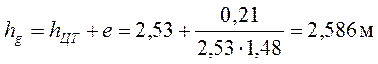
Ответ: , .

Задача №4

Определить растягивающее усилие воспринимаемое болтами полусферической крышки резервуара (рисунок 4), если показание манометра, установленного на глубине h = 3,4 м, равно р_м = 20 м вод.ст. (2 ат. = 202650 Па), радиус крышки R = 4,8 м и плотность бензина ρ = 700 кг/м³ .

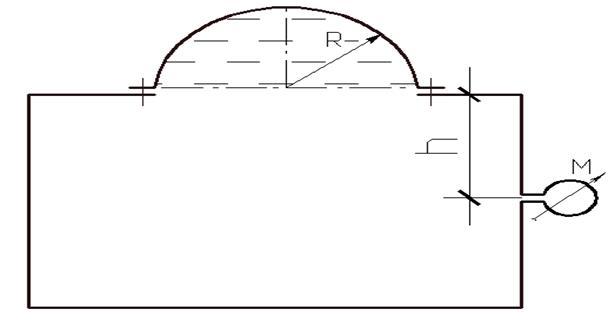
Рисунок 4

Решение:

запишем уравнение для определения усилия Р_z, воспринимаемое болтами полусферической крышки

, где  V – объем тела давления заключенный в области ABDC, т.е. между пьезометрической плоскостью и полусферической крышкой