19. В данный треугольник вписать прямоугольник с данным отношением сторон так, чтобы две его вершины лежали на основании, а две другие – на боковых сторонах треугольника.
20. Построить трапецию, если известно отношение ее оснований, углы при основании и высота.
21. Построить параллелограмм, если известны угол, отношение сторон и диагональ.
22. Построить прямоугольный треугольник по его высоте, проведенной из вершины прямого угла, и отношению квадратов катетов.
23. Построить четырехугольник с данными углами, отношением двух смежных сторон и периметром.
24. В данную окружность вписать треугольник, подобный заданному.
25. На заданной прямой построить точку, равноудаленную от заданной точки и другой заданной прямой.
Таблица 5
|
Вар |
k |
ε |
α |
a |
B |
Номера задач |
|
1 |
– 2 |
– 1 |
+300 |
4 |
-1 |
1, 16 |
|
2 |
+3 |
+1 |
–300 |
-4 |
2 |
2, 17 |
|
3 |
+2 |
– 1 |
–300 |
3 |
-4 |
3, 18 |
|
4 |
– 3 |
+1 |
+300 |
-2 |
-2 |
4, 19 |
|
5 |
+1,5 |
– 1 |
–300 |
5 |
1 |
5, 20 |
|
6 |
– 2 |
+1 |
+600 |
-1 |
-5 |
6, 21 |
|
7 |
+3 |
– 1 |
–600 |
6 |
3 |
7, 22 |
|
8 |
+2 |
+1 |
–600 |
-4 |
2 |
8, 23 |
|
9 |
– 3 |
– 1 |
+300 |
3 |
-3 |
9, 24 |
|
10 |
+1,5 |
+1 |
–300 |
-2 |
1 |
10, 25 |
|
11 |
– 2 |
– 1 |
+600 |
4 |
-4 |
11, 17 |
|
12 |
+3 |
+1 |
–300 |
-3 |
6 |
12, 18 |
|
13 |
+2 |
– 1 |
–300 |
-6 |
2 |
13, 16 |
|
14 |
– 3 |
+1 |
+300 |
-1 |
4 |
14, 21 |
|
15 |
+1,5 |
– 1 |
–600 |
2 |
-4 |
15, 22 |
|
16 |
– 2 |
+1 |
+600 |
-4 |
3 |
16, 5 |
|
17 |
+3 |
– 1 |
–300 |
-2 |
-2 |
17, 6 |
|
18 |
+2 |
+1 |
–300 |
1 |
5 |
18, 7 |
|
19 |
– 3 |
– 1 |
+300 |
-5 |
-1 |
19, 8 |
|
20 |
+1,5 |
+1 |
+600 |
3 |
6 |
20, 9 |
|
21 |
– 2 |
– 1 |
–600 |
2 |
-4 |
21, 10 |
|
22 |
+3 |
+1 |
–600 |
-3 |
3 |
22, 11 |
|
23 |
+2 |
– 1 |
–300 |
1 |
-2 |
23, 12 |
|
24 |
– 3 |
+1 |
+300 |
-4 |
4 |
24, 13 |
|
25 |
+1,5 |
– 1 |
–300 |
6 |
-3 |
25, 14 |
|
k |
ε |
α |
a |
B |
Вопросы для повторения к главе 2.
1) Является ли поворот плоскости подобным преобразованием ?
2) Дайте одно из возможных определений гомотетии в терминах элементарной геометрии (без употребления векторов) .
3) Какое преобразование является обратным к центрально-подобному вращению ?
4) Может ли гомотетия считаться частным случаем:
а) центрально-подобного вращения?
б) центрально-подобной симметрии?
5) Можно ли утверждать, что композиция двух гомотетий с общим центром равносильна некоторой гомотетии? Может ли она оказаться тождественным преобразованием?
6) Может ли подобное преобразование с коэффициентомk = 3 не иметь неподвижных точек?
7) Приведите примеры подобных преобразований с коэффициентом k = 2 , имеющих инвариантную прямую. Сколько всего таких подобий существует?
8) Может ли какое-нибудь подобное преобразование плоскости иметь аналитическое представление
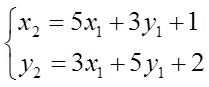 ?
?
9) Какого типа задачи на построение легко решаются с применением гомотетии?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.