


§ 1. 7. Задания для самостоятельной работы
В этом параграфе приводятся условия упражнений, которые нужно выполнить индивидуально, выбирая из 25 вариантов свой.
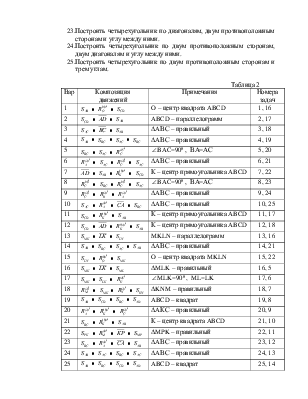
Упражнение 1. Определить название и параметры простейшего движения плоскости, равносильного заданной композиции движений (условие – в таблице 2). Указание: нужно вначале выяснить, меняет ли это движение ориентацию фигур; затем построить образы некоторых точек, чтобы применить рассуждение одной из двух теорем из §1.4.
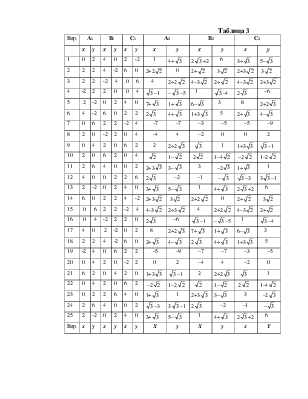
Упражнение 2. Найти аналитическое представление движения плоскости , отображающего точки А1 , В1 , С1 соответственно в точки А2 , В2 , С2 (их координаты заданы в таблице 3). Определить тип этого движения и выявить его числовые параметры. Указание: изобразив треугольники, уточнить род движения (первый или второй); далее воспользоваться структурой системы (6)( §1.3), имея найденное значение ε (-1 либо 1); подставляя в левую и правую части уравнений (6) значения «новых» и «старых» координат заданных точек, можно вычислить коэффициенты соsα, a и b . Тип и параметры движения находятся так же, как в упражнении 1.
Упражнение 3. Задать произвольный прямоугольник АВСD, символизирующий биллиардный стол и внутри него произвольную точку М (биллиардный шар). Затем построить траекторию качения шара «от двух бортов в лузу», то есть нарисовать трехзвенную ломаную с началом в М и концом в вершине прямоугольника учитывая, что удар о борт происходит по закону «угол падения равен углу отражения». Указание: воспользоваться методом зеркальной симметрии. Дополнительное упражнение (не обязательное): построить траекторию «от трех бортов в лузу».
Упражнение 4. Применяя движения плоскости, решить из приводимого ниже набора две задачи. Номера указаны в последнем столбце таблицы 2. Примечание: в учебном пособии [3] задачи 1-15 посвящены методу поворота, а остальные – параллельному переносу.
Задачи на применение движений .
1. Построить квадрат, если известен его центр и две точки, лежащие на параллельных сторонах.
2. Даны две прямые и точка. Построить отрезок с концами на данных прямых, делящийся данной точкой пополам.
3. Построить равносторонний треугольник так, чтобы три его вершины лежали на трех данных прямых.
4. Построить равносторонний треугольник так, чтобы три его вершины лежали на трех данных параллельных прямых, а центр лежал на данной четвертой прямой, не параллельной к остальным.
5. Построить равносторонний треугольник так, чтобы три его вершины лежали на трех данных концентрических окружностях.
6. Построить равнобедренный треугольник так, чтобы вершина прямого угла лежала в заданной точке, а вершины острых углов по одной на двух данных окружностях.
7. Построить равнобедренный треугольник так, чтобы вершина прямого угла лежала в заданной точке, а вершины острых углов по одной на двух данных прямых.
8. Построить квадрат, три вершины которого лежали бы на трех данных параллельных прямых.
9. На сторонах данного квадрата ABCD найти такие точки Х и У, чтобы треугольник АХУ был равносторонним.
10. Дан квадрат и точка на одной из его сторон. Построить равносторонний треугольник так, чтобы одна его вершина лежала в данной точке, а две другие – на сторонах квадрата.
11. Построить равносторонний треугольник так, чтобы одна его вершина лежала на данной окружности, другая – на данной прямой, а третья – в данной точке.
12. Построить равносторонний треугольник, одна из вершин которого лежит в данной точке, а две другие – по одной на данных окружностях.
13. Построить параллелограмм, две противоположные вершины которого лежат в данных точках, а две другие – по одной на двух данных окружностях.
14. Построить параллелограмм, две противоположные вершины которого лежат в данных точках, а две другие – по одной на двух данных прямых.
15. Построить параллелограмм, две противоположные вершины которого лежат в данных точках, а две другие – по одной на данной прямой и данной окружности.
16. Построить трапецию, зная все ее стороны.
17. Построить трапецию по диагоналям, углу между ними и одной из боковых сторон.
18. Построить трапецию по диагоналям, углу при основании и средней линии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.