














2. Расчет моста по варианту 3.
2.1. Проезжая часть.
Проезжая часть с ездой без балласта (на деревянных поперечинах).
В соответствии с действующими нормами мостовые поперечины при езде без баласта должны иметь сечение 20x24см и длину 3,25м. При этом расчетные проверки элементов проезжей части можно не производить.
2.2. Расчет составного пакета на колодках.
2.2.1 Определение усилий
Прогоны балочного моста рассчитываются как простые разрезные балки. За расчетный пролет принимается расстояние между осями насадок (рис.1).
![]()
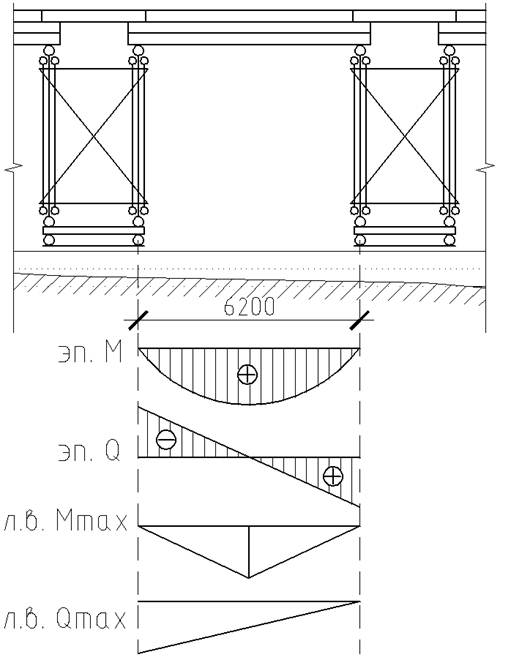 рис.1
рис.1
Нормативные постоянные нагрузки на 1 п.м. длины прогона равны:
-от веса мостового полотна на поперечинах без тротуаров:
рмп=6,68 кН/м
-от веса двух тротуаров с перилами:
рт=1,37 кН/м
-нагрузка от собственного веса прогонов определяется:
рпр= Vпр ·γd / l , где
- Vпр = 0,8 м³ – объем древесины прогона;
- γd =5,88 кН/м³– удельный вес непропитанной древесины;
- γf =1,2 – коэффициент надежности по нагрузке для деревянных конструкций и мостового полотна с ездой на поперечинах;
- l=7,5 м – длина прогона;
- d=32 cм – диаметр одного бревна в пакете;
- nб=6 – кол-во бревен в пакете;
- n – кол-во пакетов в прогоне;
- Vпр=(Πd2/4)· nб ·n·l=7,23 м³;
Рпр=(7,23 м³* 5,88 кН/м³)/7,5 м =5,96 кН/м
Интенсивность временной железнодорожной нагрузки равна:
рν =ν·К, где
- ν – интенсивность эквивалентной нагрузки;
- К=8 – класс временной нагрузки;
λ=7,5 α=0,5 → ν=16,25
рν1= рν2=16,25·8=130кН/м
Коэффициент надежности по нагрузке для временной нагрузки может быть определен по формуле:
γfν=1.3-0.003·λ=1,3-0,003·7,5=1,278
Максимальный момент в середине пролета прогона:
M=[ γf(рмп+ рт+ Рпр)+ γfν(1+μ) рν1]·l2/8 = [1,2(6,68+1,37+5,17)+1,278·1,1·130]·7,52/8=1402,68 кНм
Максимальная поперечная сила в опорном сечении:
Q=[ γf(рмп+ рт+ Рпр)+ γfν(1+μ) рν2]·l/2 = [1,2(6,68+1,37+5,17)+1,278·1,1·130]·7,5/2=748,1 кНм
2.2.2 Подбор сечения
В составных пакетах на колодках работа сечения, как единого целого достигается постановкой колодок между бревнами пакета по высоте (рис.2)
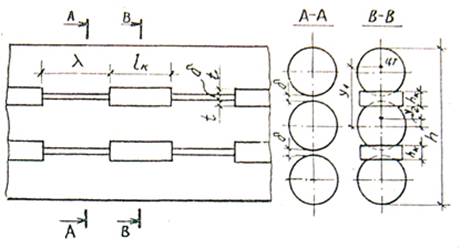 рис.2
рис.2
Требуемый момент сопротивления одного составного вертикального ряда при общем числе вертикальных рядов np, равен:
− 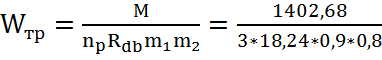 =32042,27, где
=32042,27, где
- m1=0,9 - коэф. условий работы;
- m2=0,8 - коэф. сплошности для трехъярусных пакетов;
- np=3 - кол-во вертикальных рядов;
Момент сопротивления Wnt одного вертикального ряда бревен определяется
− 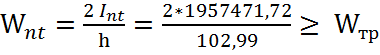 38009,16>32042,27
38009,16>32042,27
Задаваясь диметром и количеством бревен по высоте определяем момент инерции Int бревен одного ряда:
− ![]() , где
, где
- I1=29,104,54, I2=7649,36 – собственные моменты инерции соответственно крайнего и среднего бревен;
- A1=652,65– площадь сечения нетто крайнего бревна;
- y1 =38,14– расстояние от нейтральной оси до центра тяжести крайнего бревна;
Геометрические характеристики сечений бревен вычисляются по формулам:
− ![]() =0,02435*
=0,02435*![]() =25532,83
=25532,83
− ![]() =0,007295*
=0,007295*![]() =7649,36
=7649,36
− ![]() =0,63735*
=0,63735*![]() =652,65
=652,65
Расстояние от центра тяжести сечения с односторонней врубкой до центра окружности бревна равно:
− ![]() =0,0825*32=2,64
=0,0825*32=2,64
- Коэф. β1, β2, β3, β4 – зависят от соотношения t/d
Длина колодки lк должна быть не меньше 20см, а так же удовлетворять условию
− ![]()
![]() 57,50=57,50
57,50=57,50
Предполагаемая глубина врезки t=8см
Удовлетворяет условию ![]()
Несущая способность колодки из условия прочности на смятие древесины в месте врезки колодки:
− ![]() , где
, где ![]()
Aq – площадь смятия колодки
− ![]()
![]()
- Коэф. β5 – зависит от соотношения t/d
Несущая способность колодки на складывание:
− ![]() , где
, где ![]()
bk – ширина колодки;
- ma=0,8 – коэф. Условий работы;
Условно в запас прочности расчетную ширину колодки можно принять равной ширине гнезда для колодки:
− ![]()
![]()
- Коэф. β6 – зависит от соотношения t/d
За расчетную несущую способность колодки Tк берут меньшую из величин Tсм и Tск.
Tк=178,02
Необходимое кол-во колодок, устанавливаемое на половине длины пролета lр :
− 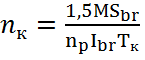 , где
, где 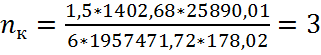
- np=3 - кол-во вертикальных рядов;
Статический момент трехъярусного ряда бревен:
− ![]()
![]() , где
, где
Площадь среднего бревна равна:
− ![]() ,
,
а расстояние от нейтральной оси до центра тяжести полусечения среднего бревна:
− ![]()
- Коэф. β7 , β8 – зависят от соотношения t/d
Расстояние между колодками λ
должно удовлетворять условию 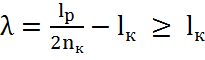
Проверка прочности древесины на складывание на участке между колодками производится по формуле:
− 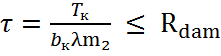
![]() 1,47
1,47
На каждую колодку действует пара сил, создающих момент, выворачивающий колодку из гнезда и раздвигающий бревна с усилием Z, равным:
− 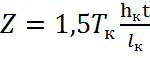 , где
, где ![]()
- hк - высота колодки;
Эти усилия воспринимаются парой вертикальных стяжных болтов, диаметр которых выбирается из условия прочности болта:
− 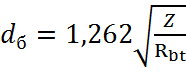
![]()
Расчетное сопротивление Rbt для болтов из стали ВСт3сп4 равно Rbt = 155МПа
По итогам подбора имеем:
Древесина основных элементов моста – лиственница:
- Rdb = 18,24 МПа –для бревен естественной коничности;
- Rdb = 16,44 МПа –для окантованных бревен;
- Rdam = 1,47 МПа;
- Rdqs = 14,16 МПа;
- Rdс = 14,16 МПа;
- Rdq = 1,47 МПа;
Требуемый момент сопротивления Wтр = 21361,51м3
Диаметр бревен в пакете d = 32 см
Глубина врезки колодок t = 8 см
Соотношение t/d = 0,25 →
β1 = 0,02435, β2 = 0,007295, β3 = 0,63735, β4 = 0,0825, β5 = 0,147325, β6 = 0,9 β7 = 0,4893, β8 = 0,1245;
Момент инерции крайнего бревна J1 = 25532,83см4
Момент инерции среднего бревна J2 = 7649,36 см4
Площадь сечения крайнего бревна A1 = 652,65см2
Расстояние от центра тяжести крайнего бревна до центра окружности бревна y = 2,64 см
Расстояние между бревнами δ = 3,5 см
Расстояние от нейтральной оси до центра тяжести крайнего бревна y1 = 38,14 см
Момент инерции бревен одного ряда Int = 1957471,72 см4
Момент сопротивления бревен одного ряда Wnt = 38 009,16 см3
Проверка по условию прочности: Wnt ≥ Wтр (38 009≥32042,27)
Длина колодки lк = 57,50 см
Площадь смятия Aq = 150,86 см2
Несущая способность древесины из условия прочности на смятие Tсм = 178,02кН
Ширина колодки bк = 28,8 см
Несущая способность древесины из условия прочности на скалывание Tск = 194,75 кН
Расчетная несущая способность колодки Tк = 178,02 кН
Расстояние от центра тяжести полусечения среднего бревна до нейтральной оси y2 = 3,98 см
Площадь сечения крайнего бревна A2 = 501,04 см2
Статический момент трехъярусного ряда бревен Sbr = 25 890,01 см3
Необходимое количество колодок, устанавливаемое на половине длины пролета nк = 3
Расстояние между колодками λ = 67,50 см
Расстояние между колодками
λ удовлетворяет условию 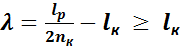 (67,50 > 52,50)
(67,50 > 52,50)
Проверка прочности древесины на скалывание на участке между колодками
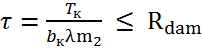 (0,11 ≤ 1,47)
(0,11 ≤ 1,47)
Высота колодки hк = 19,50 см
Усилие пары сил, выворачивающих колодку из гнезда Z = 7,24 кН
Диаметр вертикальных стяжных болтов dб = 9мм
2.3. Расчет опирания прогонов.
Проверка прочности балки на смятие в месте опирания на насадку производиться по формуле:
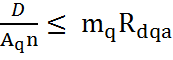 , где
, где
- D – давление, передаваемое на насадку прогонами;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.