Расчет моста с проезжей частью с ездой без балласта (на деревянных поперечинах), страница 2

-  Aq – площадь опирания одного прогона на насадку;

-  n – число прогонов;

-  mq = 1 – коэф. Условий работы;

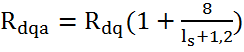-   – расчетное сопротивление местному смятию древесины;

-  ls – длина площадки смятия вдоль волокон;

c=2,5 м – ширина опоры по фасаду;

(1+μ) = 1,2 – динамический коэф.;

D = [ γ_f(р_мп+ р_т+ Р_пр)+ γ_fν(1+μ) р_ν]·(l+c)/2 = [1,2(6,86+1,37+5,96)+1,278·1,2·130]·10/2=1080,89 кНм

Rdqa = 2196,5 МПа    Aq = 0,10 м²

Проверка прочности на смятие 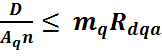 выполняется (1623,4748 ≤ 2196,5)

2.4. Расчет опор.

2.4.1 Определение усилий

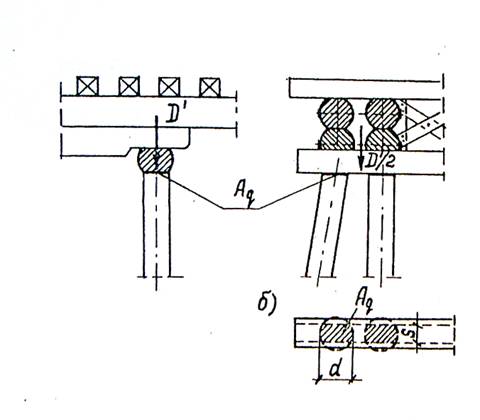
Вертикальное давление на опору определяется в соответствии со схемой на р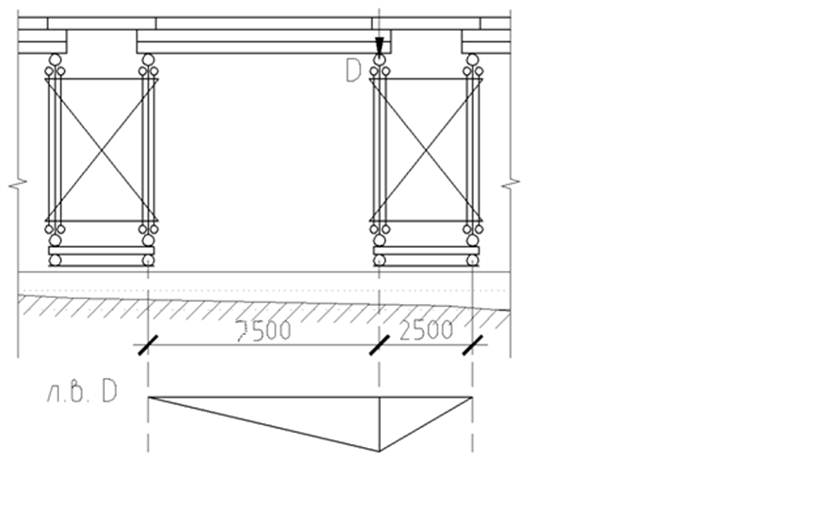ис.3.

рис.3

Нормативные нагрузки от веса мостового полотна, тротуаров, прогонов и коэффициенты надежности к ним, а также нормативная временная нагрузка и нормативная железнодорожная нагрузка определены  при расчете прогонов (см.п.2.2.1).

Коэффициент надежности по нагрузке для временной нагрузки может быть определен по формуле:

γ_fν=1.3-0.003·λ=1,3-0,003·6,5=1,278

Коэффициент динамики  для расчета элементов деревянных мостов под железную дорогу принимается равным (1+μ) =1,1;

Величина расчетного опорного давления:

D = [ γ_f(р_мп+ р_т+ Р_пр)+ γ_fν(1+μ) р_ν]·ω= [1,2(6,68+1,37+5,96)+1,278·1,1·156,3]·5 =1182,68 кН

Вес опоры:16,81

Qоп = γf1∙γd∙Vоп = 1,281∙5,88∙7,67 = 57,77 кН

-  Vоп – объем древесины опоры, без учета основания;

2.4.2 Расчет насадки на изгиб.

Насадка рассчитывается на изгиб как разрезная балка с пролетом, равным расстоянию между осями стоек опоры lнс. Давление прогонов принимают в виде равномерно распределенной нагрузки интенсивностью pнс=D/(nнс∙b), где

-  D = 1182,68 кН – расстояние между осями крайних прокладных брусьев;

-  b = 0,32 м – расстояние между осями крайних прокладных брусьев;

-  nнс = 1 – кол-во насадок, на которые передается давление;

pнс = 2798,15 кН/м

lнс = 2,5 м

Расчетный момент в сечении посередине пролета насадки

Мнс = pнс∙ l²нс/8 = 2186,06 кНм

Прочность насадки на изгиб проверяют по формуле:

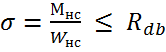 , где

-  Rdb = 2,214 МПа

-  Wнс = 3276,8 см³

σ = 18,24МПа

Проверка прочности насадки на изгиб 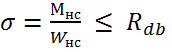выполнняется (0,66 ≤ 2,214)

2.4.3 Расчет опирания насадки на стойки.

Насадка проверяется на смятие поперек волокон в местах опирания на стойки. На соединение действует давление D’ , которое определяется по формуле:

D’ = [ γ_f(р_мп+ р_т+ Р_пр)+ γ_fν(1+μ) р_ν]·ω ,

при динамическом коэф. (1+μ) = 1,2

рис.4

D’ = [ γ_f(р_мп+ р_т+ Р_пр)+ γ_fν(1+μ) р_ν]·ω= [1,2(6,68+1,37+5,96)+1,278·1,2·156,3]·5 =1080,89 кН

Условие прочности:Rdqa = 2196,5 МПа   

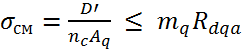 , где

-  nc  =4 – кол-во стоек, воспринимающих давление;

-  Rdqa = 2196,5 МПа – расчетное сопротивление смятию насадки поперек волокон;

-  ls = 0,22 м – длина площадки смятия вдоль волокон;

-  mq = 1,2 – коэф. условий работы древесины насадок на смятие поперек волокон;

-  Aq = 0,92dS = 0,3 м²– площадь смятия насадки стойкой;

σсм  = 655

Условие прочности выполняется 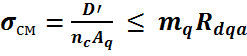 (2360 ≤ 2635)

2.4.4 Расчет стоек опоры.

Стойки опоры рассчитываются на суммарное давление от прогонов D, вычисляемое по формуле, и от веса опоры Q_оп.

-  D = 899 кНм

-  Qоп = 57,77  кН

Условие прочности сечения стойки на сжатие с учетом продольного изгиба записывается в ви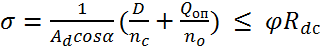де:

 , где

-  A_d=0,08 м² – площадь поперечного сечения одной стойки;

-  n_c = 6 – число стоек опоры, воспринимающих давление D;

-  n_o=12 – полное число стоек опоры;

-  α=14^о – угол наклона стоек к вертикали;

σ = 2605 кН/м²

φ – коэф. понижения несущей способности сжатого элемента;

Коэффициент φ определяется в зависимости от гибкости стойки:

 , где

-  l0 = 3,52 м – свободная длина стоек (расстояние между узлами связей);

-  i = 0,107 м – радиус инерции поперечного сечения;

λ = 32,9 → φ = 1 – 0,8(λ/100)² = 0,9134

φ∙Rdc = 10778,6 кН/м²

Проверка прочности сечения стойки на сжатие с учетом продольного изгиба

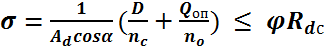выполняется (1991,76 ≤10778,6)

2.5. Проверка устойчивости опоры поперек моста.

Устойчивость опоры проверяется при поперечной ветровой нагрузке, действующей на фасадные поверхности прогонов, опоры и временные нагрузки, если она находится на мосту.

Схема действия на мост поперечной ветровой нагрузки – см.рис.5.

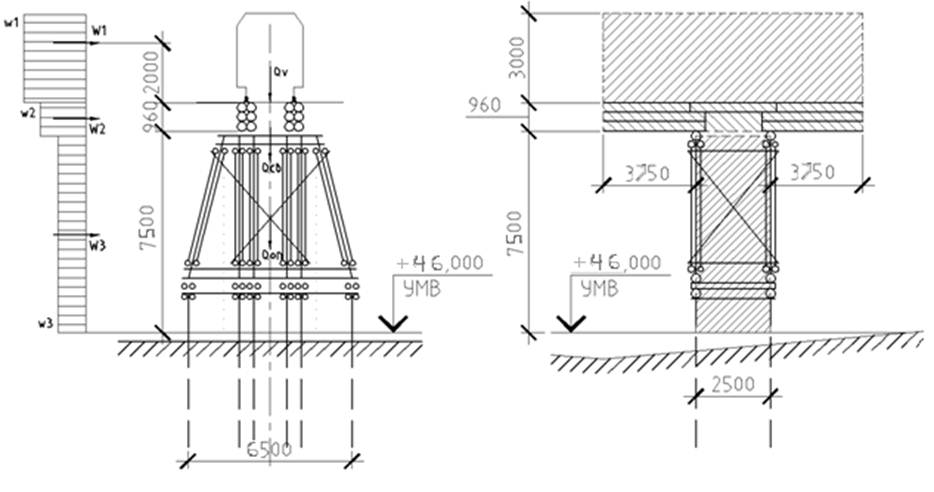
Рис.5

Интенсивность ветровой нагрузки определяется:

 , где

-  γ_f =1,5 – коэффициент надежности по нагрузке для ветровой нагрузки;

-  q_o=0,69 кПа – скоростной напор ветра;

-  k_h – коэффициент учитывающий высоту положения конструкции над поверхностью земли или горизонтом меженной воды;

-  c_w – аэродинамический коэффициент, принимаемый для башенных опор c_w=3,2; для всех остальных конструкций и временной нагрузки на мосту (приближенно) c_w= 1,85;

Интенсивность ветровой нагрузки для:

§  w₁=1,50,69 кПа1,051,85=2,01 кПа – временной нагрузки;

§  w₂=1,50,69 кПа0,891,85=1,70 кПа – пролетного строения;

§  w₃=1,50,69 кПа0,843,2=2,78 кПа – пространственной опоры;                                                                                                                          

-  l₁=l₂=7,5м. – расчетные пролеты, справа и слева от рассчитываемой опоры;

-  с=2,5м. – ширина пространственной опоры;

-  h_стр=0,96м. – строительная высота;

Ветровое давление на фасадную поверхность временной железнодорожной нагрузки на мосту:

W₁=3w₁(l+c)=3∙2,01∙10=60,30 кН

Прогонов и проезжей части:

W₂=w₂h_стр(l+c)= 1,70∙0,96∙10=16,32 кН

Промежуточной опоры:

W₃=w₃A_оп;

A_оп = 0,5ch_оп=0,5∙2,5∙7,5=9,375м²

W₃=2,78∙9,375=26,06 кН

От опрокидывания опору удерживает собственный вес прогонов, мостового полотна, опоры и вес временной вертикальной нагрузки, если она находится на мосту.

Вес прогонов и мостового полотна, передающийся на опору, определяется:

Qсв=γf∙nпр∙(pмп+pпр)∙(l+c)=0,9∙1∙12,64∙10=113,76 кН

Вес опоры деревянного моста без свайного основания равен:

Qоп=γf∙Vоп∙ γd =0,9∙7,67∙5,88=35,29 кН

В качестве временной вертикальной нагрузки на железнодорожном мосту рассматривается порожний подвижной состав с интенсивностью распределенной нагрузки v=13,7 кН/м. Передающееся на опору давление от подвижного состава:

Qv=13,7∙γfv∙(l+c)=13,7∙1∙10=137 кН

Опрокидывание опоры может произойти относительно крайней точки опирания ее на основании.

 Момент опрокидывающих сил относительно крайней точки:

Muo=ηw[W1(hоп+hстр+2)+W2(hоп+hстр/2)+W3(hоп/2)] , где

-  η_w – коэффициент сочетания ветровой нагрузке, принимаемый равным;

-  η_w=0,5 – при  временной ветровой нагрузке;

-  η_w=1,0 – при отсутствии временной нагрузке на мосту (в этом случае W₁=0)

Момент опрокидывающих сил при временной нагрузке (η_w=0,5):

Muo=429,3375 кНм

Момент опрокидывающих сил без временной нагрузки (η_w=1,0):

Muo=227,995 кНм

Момент удерживающих сил:

Mzo=(Qсв+Qоп+Qv)∙B/2

Необходимая по устойчивости ширина опоры B находится  из выражения:

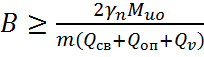 , где

-  m=1 – коэф. Условий работы;

-  γn=1,1 – коэф. надежности по назначению;

Ширина B с учетом временной нагрузки:

B ≥ 3,3 м

Ширина B без учета временной нагрузки:

B ≥ 1,75 м

Необходимая по устойчивости ширина опоры обеспечена (6,5 ≥3,3)