


















Балтийский Государственный Технический Университет им. Д.Ф.Устинова
«ВОЕНМЕХ»
.
Курсовая работа по электротехнике.
Тема:
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.
Вариант №14-200
Студент: В
Группа: Н-261
Преподаватель:
Санкт-Петербург
2008г.
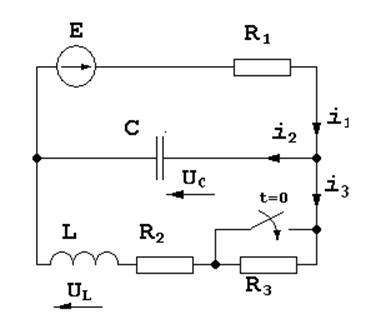
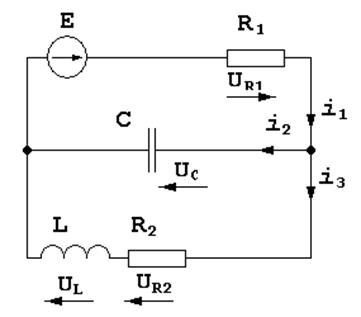
E = 200 B
L = 0.05 Гн
R1 = 500 Ом
R2 = 140 Ом
R3 = 360 Ом
C = 1 мкФ
Требуется:
1. Найти законы изменения токов и напряжений на емкости и индуктивности. Задачу решить классическим и операторным методами.
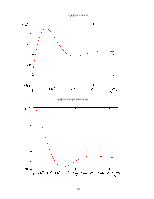
2. Построить временные диаграммы токов и напряжений.
3. Составить математическую модель переходного процесса по методу переменных состояния и подготовить систему дифференциальных уравнений. Полученные уравнения решить с помощью прикладных программ на компьютере.
4. Сравнить результаты расчета, полученные различными методами.
Сопротивления ![]() и
и ![]() соединены параллельно
соединены параллельно
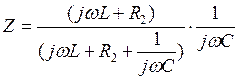 (1)
(1)
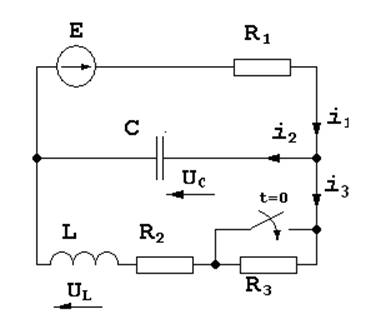
Входное сопротивление с учетом (1)
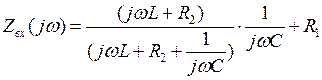 (2)
(2)
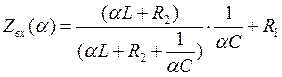 (3)
(3)
Приравняем (3) к нулю
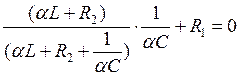
![]()
![]() (4)
(4)
![]() 1/c
(5)
1/c
(5)
![]() 1/c
(6)
1/c
(6)
Преобразуем уравнение (4)
![]() (7)
(7)
Решим уравнение (7)
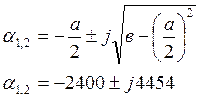
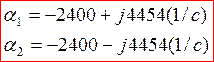
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
4. Определение начальных
условий.
Под начальными независимыми условиями понимают значения токов катушек индуктивности и напряжений на конденсаторе до коммутации.
До коммутации ток в катушке равен:
![]() (13)
(13)
Напряжение конденсатора до коммутации:
![]() (14)
(14)
Значения остальных токов и напряжений при t=0 в послекоммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, называются зависимыми начальными условиями. Составим систему уравнений для определения зависимых начальных условий:
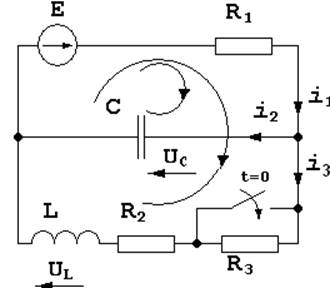
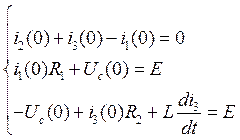 (15)
(15)
![]()
Подставим в систему независимые начальные условия:
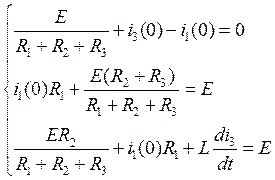 (16)
(16)
Из системы уравнений:
![]() (17)
(17)
![]() (18)
(18)
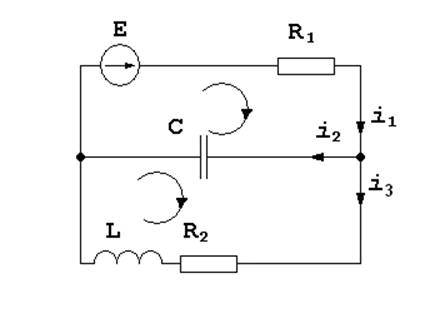
Вначале выберем условно-положительное направление токов в ветвях и направления обхода контуров. Затем запишем систему уравнений для момента времени после коммутации. Количество уравнений в системе должно быть равно числу неизвестных токов. Первое уравнение составим по первому закону Кирхгофа, второе и третье – по второму:
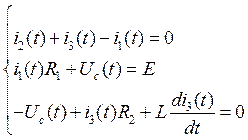
![]()
Уравнение связи для конденсатора:
![]() (24)
(24)
Полученная система уравнений сводится к одному
дифференциальному уравнению второго порядка относительно напряжения ![]()
Из уравнения (22):
![]() (25)
(25)
Уравнения (24) и (25) подставим в (21):
![]() (26)
(26)
![]() (27)
(27)
Уравнения (26) и (27) подставим в (23) и, преобразовав, получим:
![]() (28)
(28)
6. Анализ полученного ДУ.
a) Проверка размерностей коэффициентов А и В.
![]()
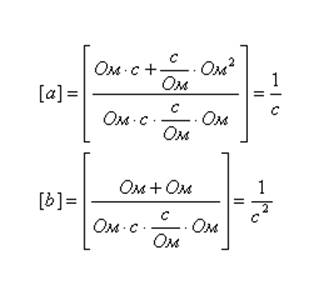
б) Проверка правой части.
При постоянном воздействии в установившемся режиме:
![]()
тогда
![]()
![]() (28)
(28)
— линейное неоднородное дифференциальное уравнение второго порядка. Известно, что решением таких уравнений является сумма двух составляющих, а именно, общего решения для соответствующего однородного уравнения и частного, полученного в форме правой части для неоднородного уравнения. Физический смысл первой составляющей – описание поведения системы при отсутствии внешнего воздействия. Эту составляющую принято называть свободной. Физический смысл второй составляющей – описание поведения системы при наличии внешнего воздействия, описываемого правой частью неоднородного уравнения. Эту составляющую принято называть принужденной. По существу, это описание нового установившегося процесса, в который должна будет перейти система после коммутации.
Таким образом, решение уравнения (28) запишется как
![]()
Принужденная составляющая
напряжения ![]() определяется в установившемся
режиме после коммутации и равна
определяется в установившемся
режиме после коммутации и равна
![]()
![]() (29)
(29)
![]() (30)
(30)
Определение постоянных интегрирования А1 и А2
В момент времени t=0:
![]()
![]()
Тогда
![]()
![]() (31)
(31)
![]()
![]()
Тогда
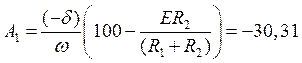
Подставив значения постоянных интегрирования получаем:
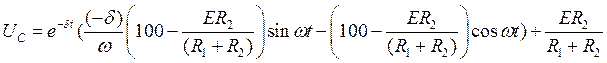 (32)
(32)
Подставим в решение численные значения корней и постоянные интегрирования определенные выше:
![]() (33)
(33)
![]()
Первый ток найдем из уравнения, составленного по второму закону Кирхгофа:
![]()
![]()
Из уравнения связи найдем ток через конденсатор:
![]()
![]()
Третий ток найдем из уравнения, составленного по первому закону Кирхгофа:
![]()
![]()
Падение напряжения на R1:
![]()
Падение напряжения на R2:
![]()
Напряжение на катушке индуктивности:
![]()
Операторная схема замещения:
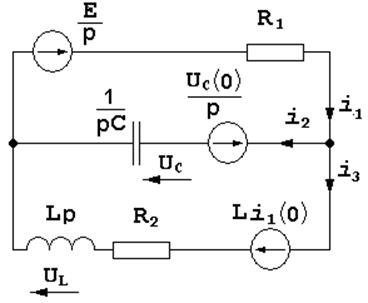
Для получения схемы замещения составляем систему уравнений по законам Кирхгофа в операторной форме:
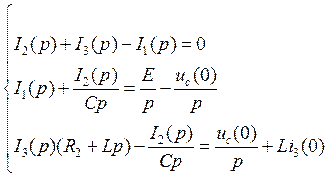
![]()
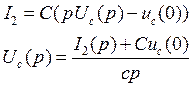 (10.4)
(10.4)
Решаем систему уравнений
относительно изображения по Лапласу искомой переменной ![]() . Решение должно быть представлено
в виде отношения двух полиномов оператора
. Решение должно быть представлено
в виде отношения двух полиномов оператора ![]() :
:
![]()
При этом необходимо, добиться
того чтобы в состав ![]() множитель при
множитель при ![]() в наивысшей степени был равен
единице.
в наивысшей степени был равен
единице.
Из уравнений (10.3) (10.1) выразим
![]() и
и ![]() :
:
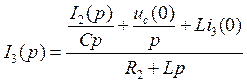 (10.5)
(10.5)
 (10.6)
(10.6)
И подставив эти уравнения в (10.2) , получим :
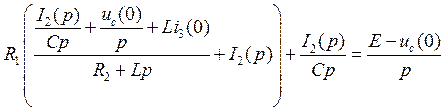 (10.7)
(10.7)
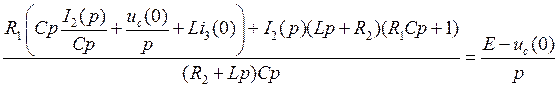
![]()
![]()
![]() (10.8)
(10.8)
Подставим (10.8) в (10.4):
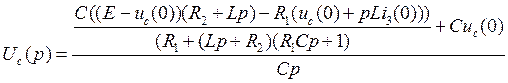 (10.9)
(10.9)
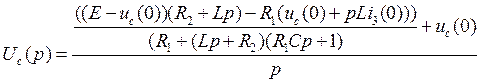
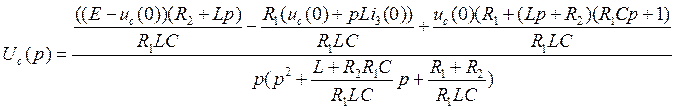 (10.10)
(10.10)
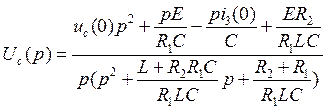 (10.11)
(10.11)
После подстановки численных значений параметров и начальных условий получим:
![]()
По теореме разложения находим оригинал – закон изменения искомой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.