Основные механические свойства и константы материалов. Модуль продольной упругости и коэффициент Пуассона

Кафедра механики деформируемого твердого тела

ПО – АО – ИТ – Р – ТЛ – НО – З – Г – Б

ПРИНЯЛ

профессор                          ( )

Лабораторная работа 1-3

Основные механические свойства и константы материалов

Группа Н-182, студент

Выдано 15.02.00.   Срок выполнения 29.02.00. Представлено

Часть 1

1. Формулировка задания

Определить модуль продольной упругости (E) и коэффициент Пуассона (m).

2. Образец:стальной стержень с прямоугольным сечением (P_max=800кгс=7800Н; толщина: h=3мм; ширина: b=25мм) Измерение продольных и поперечных деформаций (упругих) проводили датчиками омического сопротивления (С_e=5×10^-6 – коэффициент пропорциональности между относительной упругой деформацией и отсчетом по шкале деформации прибора).

3. Результаты измерений

     Таблица 1

№	Нагрузка	Степень нагрузки	Отсчеты и разность отсчетов по шкале деформации
	P, кгс	ДP, кгс	Поперечная		Продольная
			n21	Дn21	n20	Дn20
1	0	-	2137	-	2000	-
2	100	100	2140	3	1985	15
3	200	100	2144	4	1972	14
4	300	100	2148	4	1960	13
5	400	100	2152	4	1944	16

<ДP>=100

<Дn₂₁>=3.75

<Дn₂₀>=14.5

4. Вычисление модуля Юнга(E) и коэффициента Пуассона(m)

так как

e_H – относительная продольная деформация

s - нормальное напряжение

 

e₁ – относительная продольная деформация.

e₂ - относительная поперечная деформация.

5. Погрешность измерений и вычислений (для всех опытов доверительная a=0.95, t_a(3)=4.3)

  

      

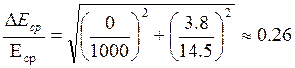
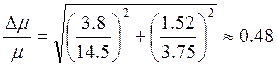
6. Вывод

Экспериментально определили модуль продольной упругости E=(1.83±0.48)×10⁵МПа и коэффициент Пуассона m=0.26+0.13 для стали. Убедились в приблизительном совпадении полученных результатов с табличными.

ЧАСТЬ 2

.

1. Формулировка задания

Построить диаграммы растяжения материалов (пластичного и хрупкого) и определить их механические свойства (условные и истинные) и константы.

2. Образец

  

 

L₀                                  

 

Параметры образцов до и после опытов.                                                          Таблица 1

Образец	Материал	Диаметр сечения		Длинна l, мм
		До	После	До	После
Пластичный	Сталь	3.8	2.1	40	53.3
Хрупкий	Серый чугун	5.8	5.8	34.7	34.7

Условные характеристики пластичного материала. Таблица 2

	Pп(предел пропорциональности)	Pт(предел текучести)	Pв(предел прочности)	Pр(момент разрыва)
Нагрузка Р, Н	1104	1447	2330	1618
Удлинение DL,мм	0,35	0,59 – 1,14	8,00	12,50

3. Предварительные определения

Площадь поперечного сечения:

,

После:

,

Напряжение:

,

Относительное удлинение:

, где L₀ длина образца до опыта ,

	sп	sт	sв	sр
Нагрузка s ,Мпа	100,4	131,5	212,0	147,1
Напряжение e	0,009	0,015-0,285	0,200	0,313

4. Решение

Нахождение истинных величин

Для хрупкого образца:

DL=0  и поэтому P_п= P_т = P_в = Р_р = 3311 Н,

s_п = s_т = s_в = s_р = 125,4 МПа , и так как y = 0 ( F* = F ), то s_и = s_р =125,4 МПа , и  e_и =0,

5. Выводы

Сравнивая полученные данные с табличными [1] можно сделать вывод о том, что мтериал пластичного образца по прочности уступает всем металлам, однако по значению пластичности (y = 68 %) приближается   к никелевому деформируему сплаву ХН55МВЦ. таким образом, можно заключить, что мы имеем дело с низко прочным, но пластичным металлом, и, следовательно, использовать его надо исходя из этих его свойств. Хрупкий же материал совершенно не пластичен и обладает прочностью меньшей, чем рассматриваемая нами ранее сталь. Следовательно, на мой взгляд, данный материал лучше не использовать, особенно в ответственных конструкциях.

Литература

1.  Плотность и механические свойства типичных металлических материалов : Приложение к лекциям 3  - 1 с.

2.  Лабораторные работы по сопротивлению материалов. Ч. 1: учебное пособие / Ф. З. Алмаметов, Л. А. Данилова, С. А. Енгалычев и др.; под редакцией Ф. З. Алмаметова. – Л.: Ленингр. мех. ин-т. 1977. – 88с.