Практические аспекты использования рядов МНК и Фурье. Методика работы с программным обеспечением, страница 2

Разложение дискретной функции F(t_i), включающей m значений, в ряд МНК означает ее приближенную замену полиномом F¢_Ч(t) следующего вида [5]: 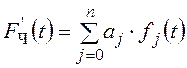, где j = 0, 1, 2 … n, n – число членов ряда МНК, t – текущее время, a_j – коэффициенты ряда МНК, f_j(t) - ортогональные полиномы (произведение усредненных значений которых на определенном интервале равно нулю). Коэффициенты ряда МНК a_j определяются методом наименьших квадратов [5]: 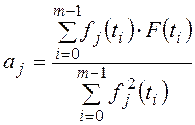. Суть метода наименьших квадратов заключается в том, что аналитическая зависимость, обеспечивающая минимизацию суммы квадратов отклонений экспериментальных значений, позволяет получить наилучшую их аппроксимацию.

Ортогональные полиномы ряда МНК определяются как [5]:

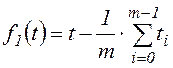;    ;    , где a_j, b_j-1 – константы, определяемые из условий ортогональности функций:

;                .

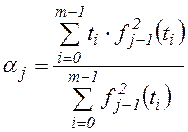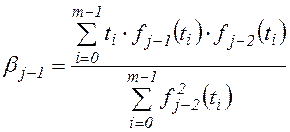При этом может быть введена величина «амплитуды» для j-го члена ряда МНК Q_j, показывающая его вклад в получаемое значение функции F¢_Ч(t): .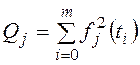

Из курса математики известно, что всякая периодическая функция, удовлетворяющая условиям Дирихле (функция имеет за полный период конечное число разрывов первого рода (скачков) и конечное число экстремумов) может быть разложена в тригонометрический ряд (ряд Фурье).

Разложение дискретной функции F(t_i), включающей m значений, в ряд Фурье означает ее приближенную замену тригонометрическим полиномом F¢_Ф(t) следующего вида [2]:

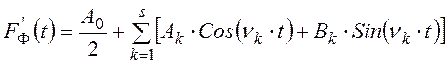, где  – число членов ряда Фурье (число гармоник),  – среднее значение функции F(t_i), 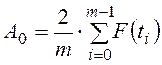,  – частота для  k-й гармоники, = 2×p×k / T, T = 2×p /w – период вращения входного звена, ,  – коэффициенты ряда Фурье, , .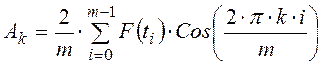

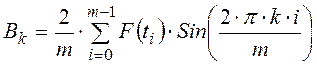При этом вводится величина амплитуды для k-й гармоники С_k, показывающая вклад каждого члена ряда Фурье в получаемое значение функции F¢_Ф(t) [2]: .

Точность аппроксимации дискретной функции F(t_i) с помощью рядов МНК и Фурье можно оценить с помощью средней относительной погрешности P: 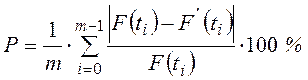, где ,  – значения в узловых точках (в моменты времени t_i) соответственно исходной дискретной и аппроксимированной функций.

Поскольку функция F(t_i) задается дискретно в виде таблицы значений в конечном числе точек  m, то предельное число членов ряда МНК n_max =  m, а ряда Фурье - n_max =  m / 2.

Однако в случае разложения функции F(t_i) в ряд МНК с числом членов n_max полученные зависимости кинематических параметров вероятнее всего не будут удовлетворительными, а в ряд Фурье с числом гармоник n_max они скорее всего не будут гладкими. Для сглаживания этих зависимостей необходимо определить рациональное число учитываемых членов рядов n_r путем анализа амплитудных спектров.

Амплитудные спектры рассматриваемых рядов МНК и Фурье представляют собой линейчатую зависимость амплитуд Q_j и C_j от порядковых номеров членов ряда.

Амплитудные спектры для рядов МНК и Фурье позволяют определить ориентировочное значение рационального числа членов ряда n_r. Для его определения визуально по графику определяют число членов ряда, при котором амплитуда становится примерно одной величины. Это число членов ряда и является рациональным.

Однако при этом для ряда МНК и Фурье необходимо также осуществлять визуальный контроль «похожести» аппроксимированной зависимости на исходную дискретную функцию. Кроме того, при аппроксимации функции указанными рядами нужно обеспечить минимизацию средней относительной погрешности.

Последние замечания предполагают возможность некоторой небольшой корректировки рационального числа членов рядов МНК и Фурье.

Учет только рационального числа членов рядов n_rпозволяет сгладить функции перемещения, скорости и ускорения за счет «отброса» высших членов и учета только низших членов рядов МНК и Фурье.

После разложения в ряд функции скорости и ускорения могут быть легко получены дифференцированием ряда.

2. МЕТОДИКА РАБОТЫ С ПРОГРАММНЫМ ОБЕСПЕЧЕНИЕМ

Обработка данных эксперимента рядами МНК и Фурье проводится с помощью программного обеспечения, разработанного для операционной системы WINDOWS произвольной версии, данное приложение запускается исполняемым модулем approxim.exe.