Метод динамики средних. Дифференциальные уравнения динамики средних. Модель высоко организованного боя

Глава 8

Метод динамики средних

8.1. Дифференциальные уравнения динамики средних

Рассмотрим систему S, состоящую из N однотипных элементов E, например, танковую роту. Пусть каждый из элементов может находиться в n различных состояниях. Ясно, что общее число различных состояний системы S равно n^N, и если N или n велико, то граф состояний системы будет необычайно громоздким, а решение уравнений Колмогорова затруднено даже на ЭВМ. Кроме того, результаты решения будут трудно обозримыми. Поэтому поставим задачу по-иному. Будем анализировать состояния отдельного элемента E, а также средние характеристики системы S.

Обозначим возможные состояния элемента E символами e₁, e₂,...,e_n. Состояние системы в целом в момент времени t будем характеризовать числом элементов X_k(t), находящихся в состоянии e_k. Ясно, что X_k(t), k=1,2,...,n - случайные функции времени. Их математические ожидания и дисперсии равны

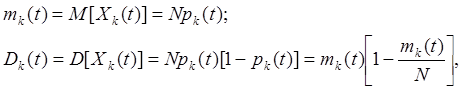               (8.1)

где p_k (t) - вероятность того, что в момент времени t отдельный элемент системы будет находится в состоянии e _k.

Дифференциальные уравнения Колмогорова для вероятностей состояний элементов имеют вид

               ( 8.2)

Умножая эту систему на число элементов N и принимая во внимание (8,1), получим дифференциальные уравнения динамики средних:

              (8.3)

Для однозначного решения этой системы одно из ее уравнений должно быть заменено нормирующим условием

В общем случае интенсивности потоков событий l_jk, переводящих элементы системы их одного состояния в другие, зависят от того, сколько элементов в данном состоянии имеется в системе. Численности X_j(t) и X_k (t) случайны, поэтому случайными оказываются и интенсивности переходов. Это затруднение преодолевается за счет допущения, носящего название принципа квазирегулярности. Принимается, что интенсивность потоков событий зависит не от самих численностей состояний, а от их средних значений (математических ожиданий):

Уравнения динамики средних (8,3) могут быть обобщены на случай, когда в ходе моделируемого процесса происходит пополнение системы S извне элементами, находящимися в том или ином состоянии. Если интенсивность пополнения системы элементами k-ого состояния  обозначить d _k(t), то уравнения (8,3) следует переписать в виде

Общее число элементов в системе в этом случае переменно

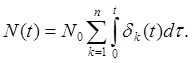
Нормирующее соотношение остается, конечно, в силе.

В качестве примера рассмотрим цех, оборудованный большим числом N однотипных станков. На каждый из них действует поток неисправностей с интенсивностью l, не зависящий от числа неисправных станков. Ремонтом станков занимается бригада рабочих. Ее производительность m, выраженная числом станков, восстанавливаемых в единицу времени, также постоянна. Каждый станок может находиться в одном из двух  состояний: e₁ - исправен, e₂- ремонтируется. Граф состояний станка показан на рис. 8.1. Средняя интенсивность потока ремонтов в расчете на один станок