Определение размеров зубчатых колёс планетарного редуктора из условия работоспособности подшипников в сателлитах. Проектирование узла сателлита

Минимальная толщина обода, обеспечивающая изгибную прочность сателлита:

h_g³0.5m×=0.5×3×=7,8 мм

12. Диаметр отверстия под подшипник:

D'=(d_f)_g -2h_g = 73,5 - 2 × 7,8 = 57,9 мм

13. Радиальная нагрузка, воспринимаемая наиболее нагруженной опорой сателлита:

F_r=4T_aW/(d_a)n_wn_m = 4×487,8×1,03/81×3×2 = 4135,3 Н

где:  число подшипников в опоре n_m=2.

14. Приведённая радиальная нагрузка:

P=VF_rK_бK_T

где: V - коэффициент вращения кольца подшипника относительно вектора нагрузки V=1,2

K_б - коэффициент безопасности

K_T - температурный коэффициент K_T=1

Параметры V, K_б, К_т приняты в соответствии с рекомендациями по подбору подшипников.

P = 1,2×4135,3×1,3×1 = 6451 Н

15. Расчётное значение динамической грузоподъёмности подшипника:

С_расч=P×[L_E/(n_зам+1) ]^1/m`/К_кач

где: n_зам - число замен подшипников за весь срок службы передачи

К_кач - коэффициент качества подшипников, зависящий от его класса точности, К_кач =1

- показатель степени, зависящий от типа подшипника, m'=3,33-роликовый подшипник, m'=3,0-шариковый подшипник,

С_расч=6451×(26,7/(0+1))^1/3,33/1=19260 H

16. По найденным значениям p' и С_расч из [1] стр. 389 выбираем подшипник:

радиально-упорный роликовый однорядный конический подшипник типа 7205 ГОСТ333-79 с параметрами: С₁=23400 Н>С_расч=19260 H

D=52 мм; d=25мм; n₁=5 000 об/мин >|n_g1-n_h1|; В=15 мм

17. Фиксирование сателлита относительно подшипников осуществляется дистанционным кольцом и стандартным пружинным кольцом IА52 ГОСТ 13941-80, устанавливаемыми между встроенными подшипниками сателлита.

18. Назначаем основные геометрические параметры щёк водила:

- D_h=m(z_a+z_g)+d+(20¼30)=3×(27+27)+25+30=217 мм;

- t_h=(0.055¼0.065)d_b=0,065×243=15,8 мм;

- t_n=(1.52)t_h=1,5×15,8=23,7 мм;

- d_h=(d_a)+10=87+10=97 мм.

Найденные значения округляем до ближайших нормальных размеров из ряда Ra40.

D_h=220 мм; t_h=16мм; t_n=24 мм; d_h=95 мм.

19. Для осевого фиксирования оси сателлита используются два пружинных кольца IБ25 ГОСТ 13940 - 80

Быстроходная ступень

1. Предложено спроектировать узел сателлита, минимальный по габаритам, удовлетворяющий критериям контактной и изгибной выносливости зубьев и работоспособности подшипника сателлита. Исходные данные представлены в таблице.

2. Определяем минимальный диаметр сателлита, обеспечивающий работоспособность встроенного подшипника. При расчете принимается эквивалентное число оборотов подшипника  млн.об.

 млн.об.

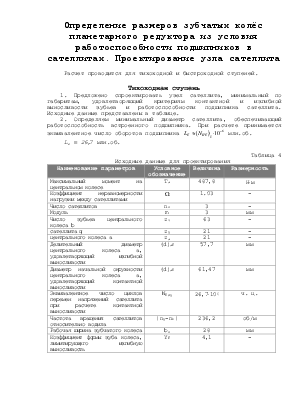
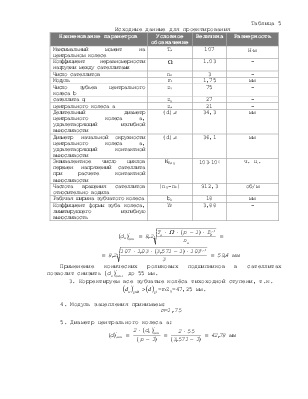
Таблица 5

Исходные данные для проектирования

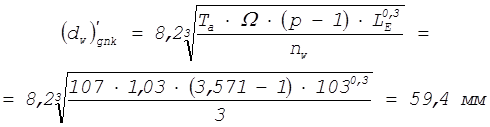
Применение конических роликовых подшипников в сателлитах позволит снизить  до 55 мм.

3. Корректируем все зубчатые колёса тихоходной ступени, т.к. =m×Z_g=47,25 мм.

4. Модуль зацепления принимаем:

m=1,75

5. Диаметр центрального колеса а:

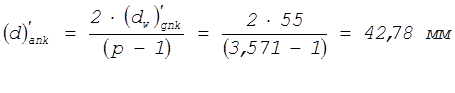
6. Число зубьев центрального колеса а:

;

Принимаем .

7. Числа зубьев  и :

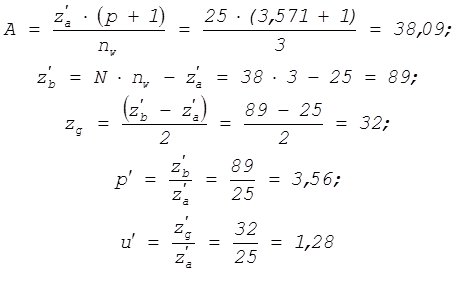
8. Корректируем рабочую ширину колёс:

поскольку , то:

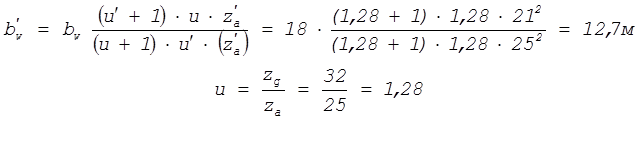
т.к.  , то принимаем мм; мм.

9. Окончательно:

Z_a=25;

Z_b=89;

Z_g=32.

10. Основные диаметры колёс планетарной ступени:

- делительный диаметр (мм)

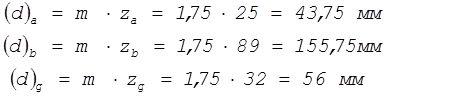
- диаметр окружности выступов (мм)

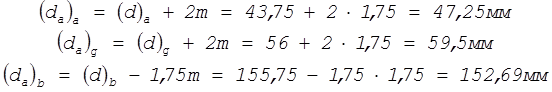
    - диаметр окружности впадин (мм)

(d_f)_a =(d)_a - 2.5m = 43,75 - 2,5 × 1,75 = 39,38 мм

(d_f)_g =(d)_g - 2,5m = 56 - 2,5 × 1,75 = 51,63 мм

(d_f)_b=(d)_b + 2,5m = 155,75 + 2,5 × 1,75 = 160,13 мм

- межосевое расстояние (мм)

a_w=0.5×[(d_a) +(d)_g ] = 0,5 ×[43,75 + 56] = 49,9мм

11. Минимальная толщина обода, обеспечивающая изгибную прочность сателлита:

h_g³0.5m×=0.5×1,75×=4,95 мм

12. Диаметр отверстия под подшипник:

D'=(d_f)_g -2h_g = 51,63 - 2 ×4,95 = 41,73 мм

13. Радиальная нагрузка, воспринимаемая наиболее нагруженной опорой сателлита:

F_r=4T_aW/(d_a)n_wn_m = 4×107×1,03/43,75×3×2 = 1679,4 Н

где:  число подшипников в опоре n_m=2.

14. Приведённая радиальная нагрузка:

P=VF_rK_бK_T

где: V - коэффициент вращения кольца подшипника относительно вектора нагрузки V=1,2

K_б - коэффициент безопасности

K_T - температурный коэффициент K_T=1

Параметры V, K_б, К_т приняты в соответствии с рекомендациями по подбору подшипников.

P = 1,2×1679,4×1,3×1 = 2620 Н

15. Расчётное значение динамической грузоподъёмности подшипника:

С_расч=P×[L_E/(n_зам+1) ]^1/m`/К_кач

где: n_зам - число замен подшипников за весь срок службы передачи

К_кач - коэффициент качества подшипников, зависящий от его класса точности, К_кач =1

- показатель степени, зависящий от типа подшипника, m'=3,33-роликовый подшипник, m'=3,0-шариковый подшипник,

С_расч=2620×(103/(0+1))^1/3,33/1=12263 H

16. По найденным значениям p' и С_расч из [1] стр. 389 выбираем подшипник:

радиально-упорный роликовый однорядный конический подшипник типа 7203 ГОСТ333-79 с параметрами: С₁=13500 Н>С_расч=12263 H

D=40 мм; d=17 мм; n₁=6300 об/мин >|n_g1-n_h1|; В=12 мм.

17. Фиксирование сателлита относительно подшипников осуществляется дистанционным кольцом и стандартным пружинным кольцом IА40 ГОСТ 13941-80, устанавливаемыми между встроенными подшипниками сателлита.

18. Назначаем основные геометрические параметры щёк водила:

- D_h=m(z_a+z_g)+d+(20¼30)=1,75×(25+32)+17+20=136,75 мм;

- t_h=(0.055¼0.065)d_b=0,055×155,75=8,57 мм;

- t_n=(1.52)t_h=2×8,57=17,14 мм;

- d_h=(d_a)+10=43,75+10=53,75 мм.

Найденные значения округляем до ближайших нормальных размеров из ряда