Динамическая схема гидросистемы. Компонентные уравнения упругого элемента. Коэффициент местных сопротивлений

Компонентное уравнение диссипативного элемента получено с учетом уравнения Навье – Стокса:

, где  - коэффициент гидравлического сопротивления, (Н*с)/м⁵:

,

где  - коэффициент линеаризации вязкого трения жидкости.

ü  Компонентные уравнения упругого элемента

, где С_г – коэффициент гидравлической жесткости, Н/м⁵:

,

Е – модуль объемной упругости жидкости, Н/м².

Топологические уравнения:

1.  Условия равновесия потенциалов: .

2.  Условие непрерывности потока: .

При    построении    динамической    модели   учтем    основные   свойства гидравлической системы, будем считать магистрали сравнительно короткими и рассматривать их, как дискретные элементы (магистрали), рассматриваем как сосредоточенную, так как длина соединительной магистрали значительно меньше магистрали потребителей, то в первом приближении массой жидкости в ней можно пренебречь.

Рисунок 2 – Схема динамической модели гидросистемы.

Внешнее воздействие на гидросистему создаются потребителями и насосами, при чем воздействие потребителей, представляет собой источники потенциалов, воздействие насосов, источники потока. Источники потенциалов описываются функциями давлений характеризующий потери напора в гидроаппарате и потребителя, а источник потока, функция расхода (подача насоса), .

Упругий элемент, учитывающий сжимаемость в газожидкостной смеси и деформация стенок трубопровода, подключают в точку ветвления гидравлической магистрали. Он осуществляет дифференциальной соединение всех инерционных элементов и источников потока. На рисунке 2 представлена схема динамической модели гидросистемы.

Ориентированный граф (орграф), позволяет идентифицировать структуру и физическое свойство моделируемой гидросистемы и представляющей собой ее математическую модель в графической форме. узлы орграфа соответствуют сосредоточенным массам. в нашем случае это пять гидравлических масс, магистрали потребителя – 1, 2 , 3, 4 , 5 и внешнее источники потока, насосы – 1*, 2*.

Рисунок 3 – Орграф гидросистемы.

Так же на орграфе отметим базовый узел с нулевым номером отображения системы отсчета системы фазовых координат типа потока. Ветви графа отображают описание: инерционных, диссипативных, упругих элементов моделей и источников внешних воздействий.

В ветвях источников внешних воздействий выберем следующие направления:

1.  От базы к 1* и 2*, т.к. расход насоса отдается гидросистеме.

2.  От 1, 2, 3 к базе, т.к. потребители забирают рабочую жидкость из системы. Всегда ветвь источника соединяет узлы с базой.

Инерционные ветви соединяют узлы, отождествляющие сосредоточенные массы с базой, направление всегда от узла  к базе.

Ветви упругих и диссипативных компонентов, соединяют между собой взаимодействующие узлы. В соответствии со схемой модели, ветви диссипативных элементов соединяют узлы с базой, т.к. база соответствует точки ветвления гидросистемы, при таком соединении направление от узла к базе.

В ветвях упругих компонентов, направление передачи энергии от источников – 1* и 2*, потребителям – 1, 2, 3.

Информация о математической модели гидравлической системы, которая содержит орграф, может быть представлена в виде матрицы. Матрица имеет размерность , где  - число строк, соответствующая узлам орграфа за исключением базы;  - число столбцов, соответствующие ветвям орграфа.

Единицами отличаются наличие соединений между узлами и ветвями, нулями – их отсутствие. Направление сигналов в ветвях отображается знаком 1 («-» сигнал направлен от узла, «+» - к узлу). Сформированная таким образом матрица носит название матрица инциденции.

Используя обозначение, механической поступательной системы и запишем, полную математическую модель на основе узлового метода:

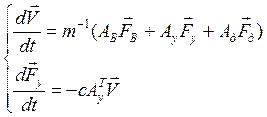, где

 - диагональные матрицы параметров инерционных, диссипативных и упругих элементов;

 - подматрицы влияния воздействия упругих и диссипативных элементов.

Запишем подматрицы ветвей источников , упругих  и диссипативных  ветвей.

, , .

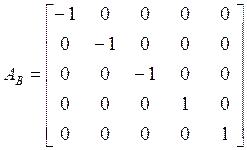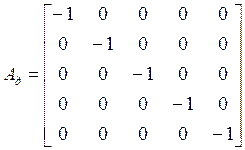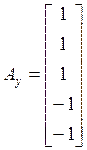Диагональная матрица параметров элементов системы:

, , .

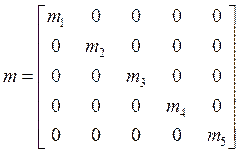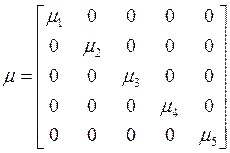Вектор потенциалов , упругих  и диссипативных  элементов:

, , .

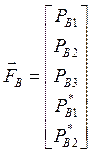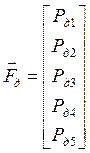Вектор фазовой переменной типа потока:

.

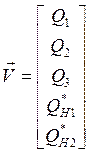Вычислим матричное произведение, учитывая, что:

, , .

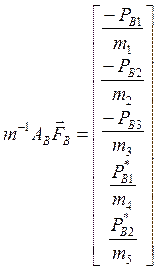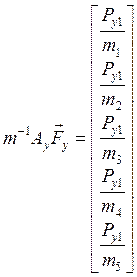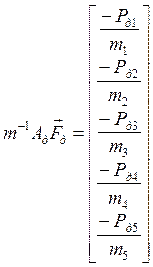Сложим полученные матрицы:

.

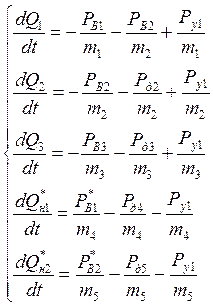Учтем, что , тогда  и  получаем вместо двух последних уравнений:

.

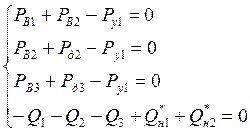Компонентное уравнение в диссипативных элементах в гидросистеме носят более сложный характер при этом выделяют линейные и нелинейные потери давления в гидромагистрали при этом их компонентные уравнения, запишутся виде:    

где µ_л- коэффициент гидравлического сопротивления, характеризующий линейные потери при ламинарном режиме движения жидкости;

µ_н- коэффициент гидросопротивления характеризующий нелинейные потери