

Вариант №28
![]()
|
|
А) Построение временных и частотных характеристик систем управления
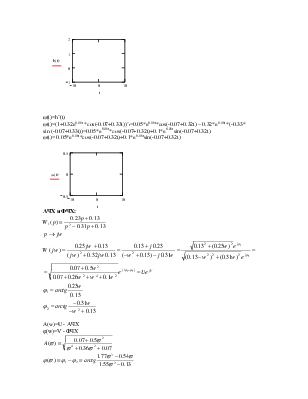
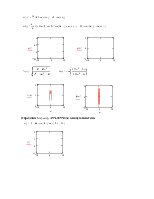
1. По заданной структурной схеме дискретной системы определить передаточную функцию зад-й системы и построить переходный процесс, приняв за входное воздействие единичный ступенчатый сигнал.
x(z)=1(t) ![]() (z)=z/(z-1)
(z)=z/(z-1)
W3=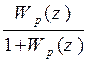
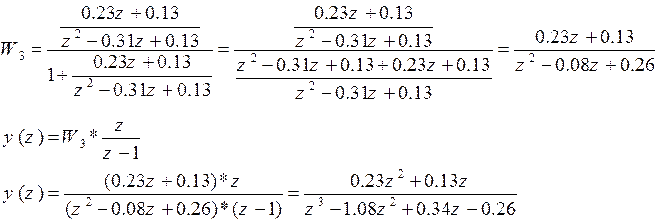
Т.е. h(z)=0.23z-1+0.38z-2-0.33z-3-0.43z-40.25z-5-0.21z-6-0.25z-7
Построим график переходной функции для дискретной системы, z[0;10]
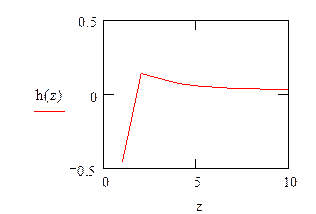
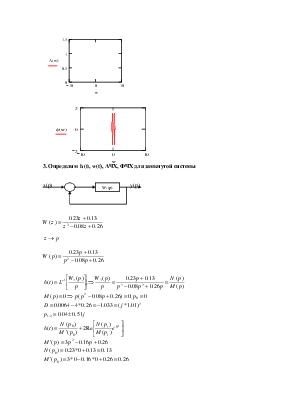
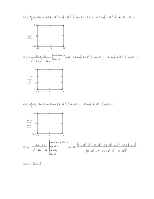
2. Из передаточной функции отбросить импульсный элемент и определить h(t), w(t), АЧХ, ФЧХ. Выражение записать аналитически и построить графики данных функций для разомкнутой системы.
z→p
![]()
|
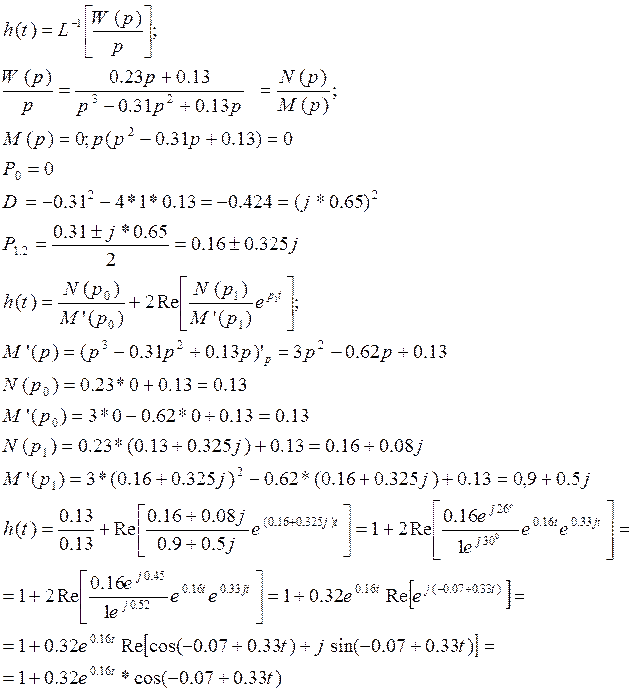
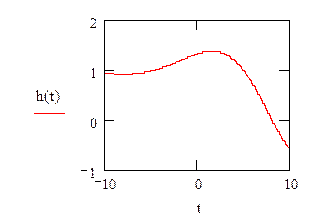
ω(t)=h’(t)
ω(t)=(1+0.32e0.16t *cos(-0.07+0.33t))’t=0.05*e0.16t*cos(-0.07+0.32t) – 0.32*e0.16t *(-0.33*
sin (-0.07+0.33t))=0.05*e0.16t*cos(-0.07+0.32t)+0.1*e0.16tsin(-0.07+0.32t)
ω(t)= 0.05*e0.16t*cos(-0.07+0.32t)+0.1*e0.16tsin(-0.07+0.32t)
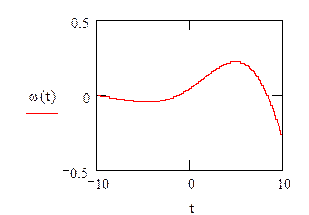
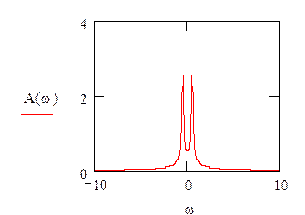
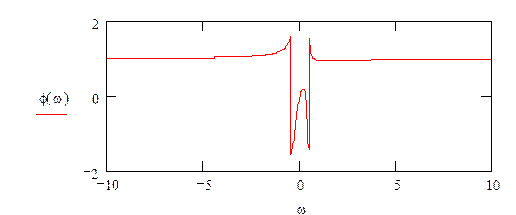
АЧХ и ФЧХ:
![]()
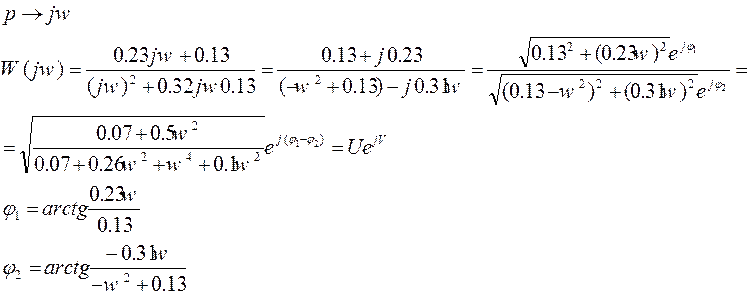
A(w)=U - АЧХ
φ(w)=V - ФЧХ
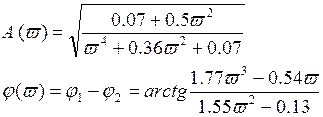
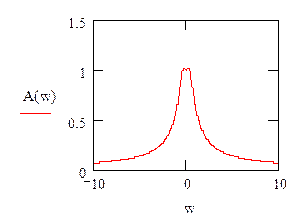
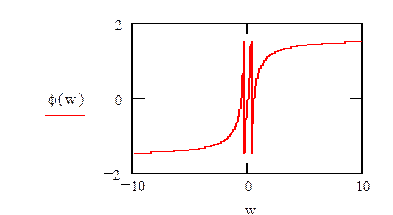
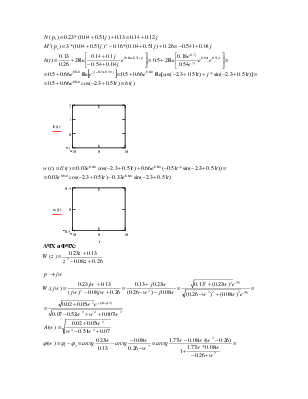
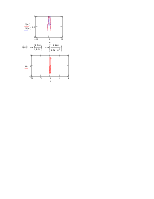
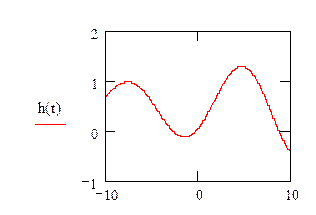
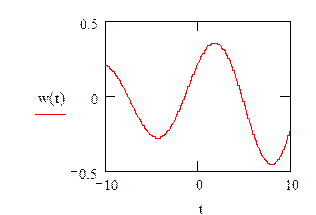
3. Определим h(t), w(t), АЧХ, ФЧХ для замкнутой системы
![]()
![]()
![]()
![]()
![]()
|
![]()
![]()
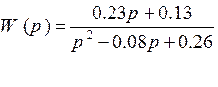
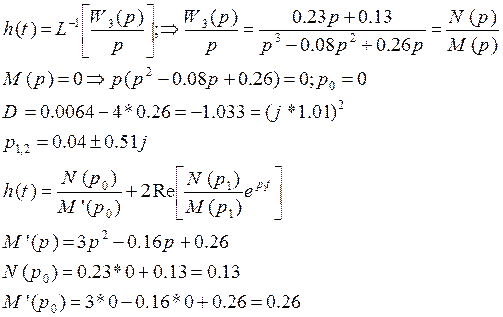
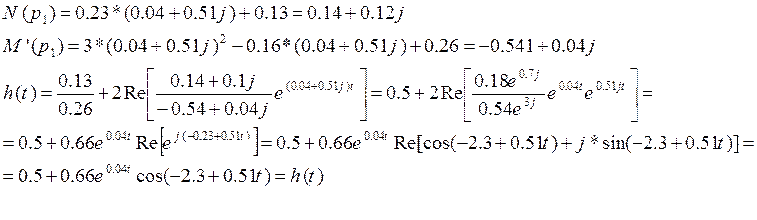
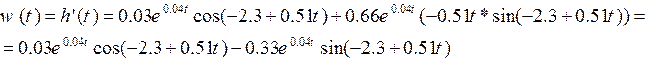
АЧХ и ФЧХ:
![]()
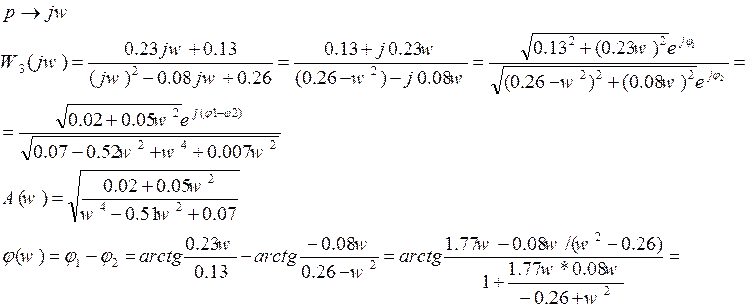
![]()
![]()
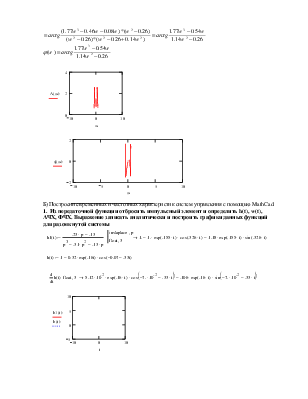
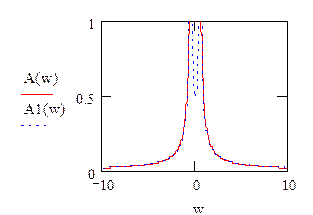
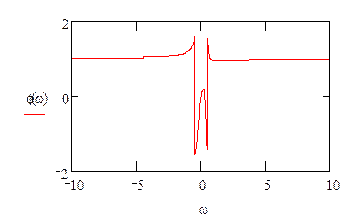
Б) Построение временных и частотных характеристик систем управления с помощью MathCad.
![]() 1. Из передаточной
функции отбросить импульсный элемент и определить h(t), w(t),
АЧХ, ФЧХ. Выражение записать аналитически и построить графики данных функций
для разомкнутой системы
1. Из передаточной
функции отбросить импульсный элемент и определить h(t), w(t),
АЧХ, ФЧХ. Выражение записать аналитически и построить графики данных функций
для разомкнутой системы
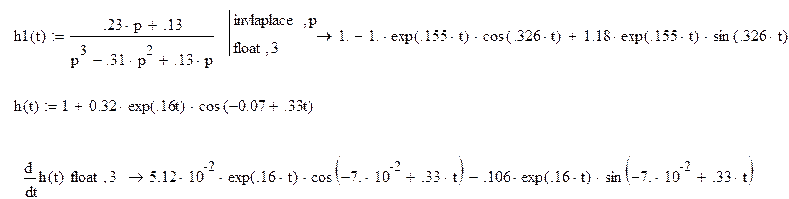
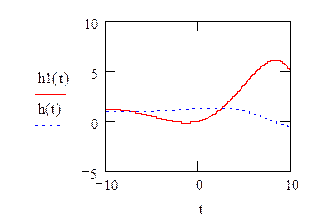
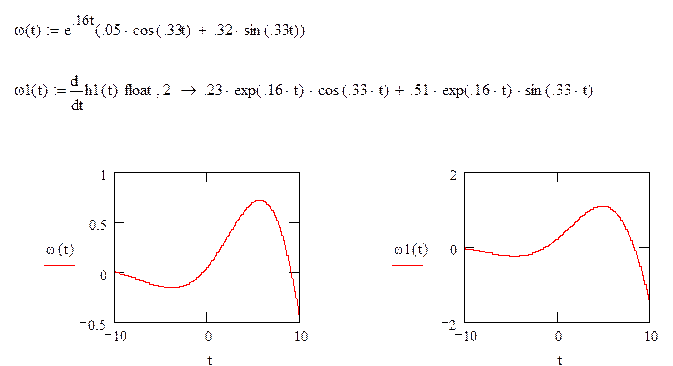
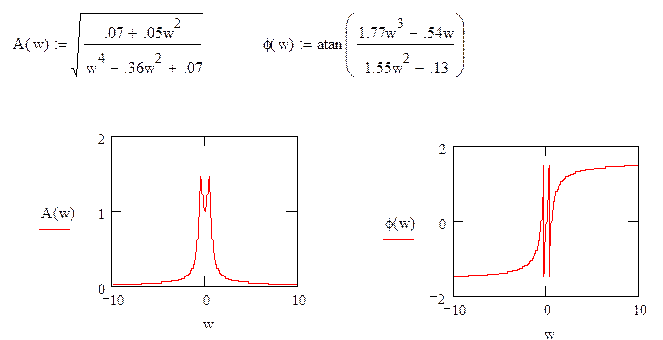
Определим h(t), w(t), АЧХ, ФЧХ для замкнутой системы
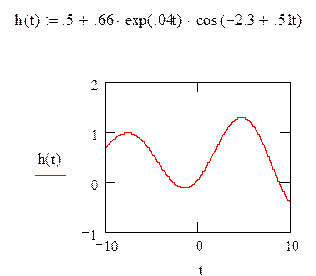
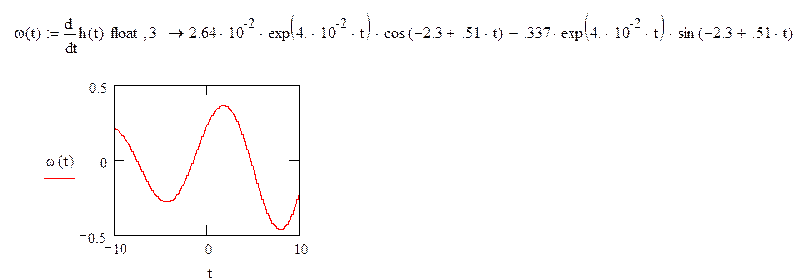
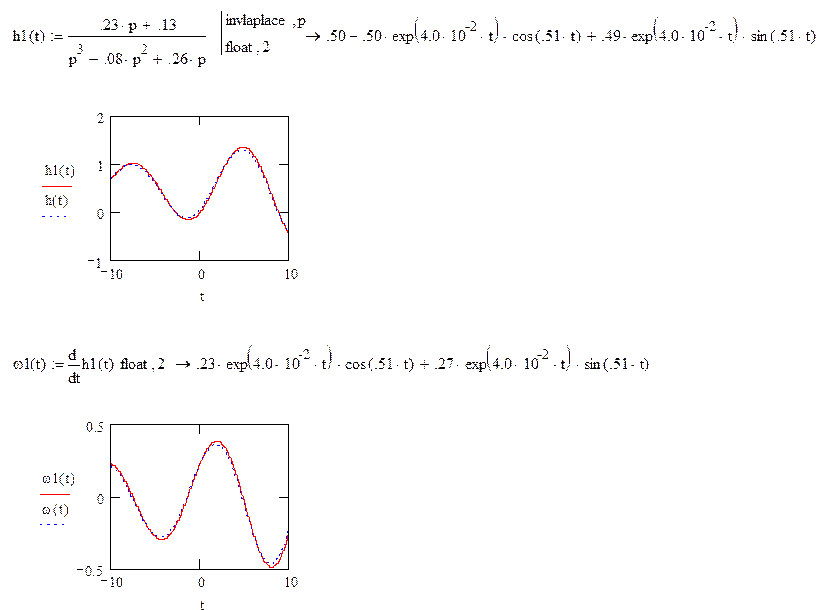
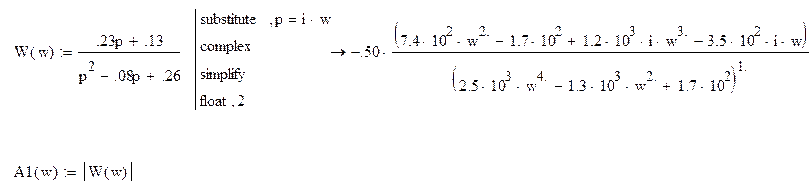
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.