Расчет проезжей части пролетных строений. Расчет главных балок пролетного строения, страница 2

                    ε_b – коэффициент, учитывающий асимметрию цикла напряжений в бетоне и

                            принимаемый в зависимости от значений ρ:

                     ε_ρs – коэффициент, учитывающий асимметрию цикла напряжений в арматуре и

                            принимаемый в зависимости от значений ρ и класса арматуры:

ρ Класс арматуры	- 1,0	- 0,5	- 0,2	- 0,1	0	0.1	0,2	0.3	0,4	0.6	0,7	0,75
А – 11 ()	0,40	0,50	0,60	0,63	0,67	0,70	0,74	0,81	0,87	1	1	1
А – 111 ()	0,32	0,40	0,48	0,51	0.54	0,57	0,59	0.65	0.70	0,81	0.90	0.95

                    β_ρω – коэффициент, учитывающий влияние на условия работы арматуры наличия

                             сварных стыков. Для соединений стержней контактной и точечной сваркой при 

                             условии механической зачистки их концов β_ρω = 1.0

              R_b и R_S – расчетные сопротивления бетона и арматуры при расчетах на прочность.

В нашем случае , и  соответственно равны 1,24; 1,24 и 1,0

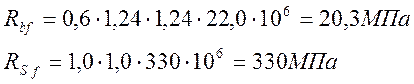
-  в бетоне

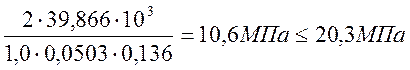
-  в арматуре

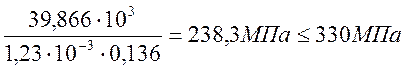
Обычно проверка напряжения в бетоне выполняется. Если напряжения в арматуре превышают расчетное сопротивление по выносливости, то требуется увеличить площадь рабочей арматуры А_S или толщину плиты.

1.2.3.     Расчет наклонных сечений плиты на прочность

Проверка прочности по поперечной силе наклонных сечений производится из условия, ограничивающего развитие наклонных трещин:

где Q_i – поперечная сила в расчетном сечении;

      R_bt – расчетное сопротивление бетона осевому растяжению.

Условие выполняется!!!

Если данное условие не выполняется и требуется поперечное армирование (отгибы, хомуты), то расчет наклонного сечения плиты на поперечную силу следует вести по формулам из раздела расчет на прочность по поперечной силе (определение расчетных усилий в главных балках пролетного строения).

1.2.4.  Расчет на трещиностойкость

Расчетом ограничивается ширина раскрытия поперечных трещин.

Определение ширины раскрытия поперечных трещин в конструкциях с арматурой периодического профиля производится по формуле

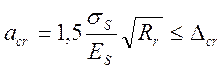
где = 0,02 см – предельное значение расчетной ширины раскрытия трещин;

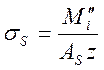            - напряжение в рабочей арматуре;

                       - изгибающий момент для расчета на трещиностойкость в расчетном сечении;

                           z – плечо пары внутренних сил, принимаемое из расчета сечения на прочность;

                         Е_S – модуль упругости ненапрягаемой арматуры, равный Е_S = 2,06ּ10⁵ МПа – для

                                 арматуры класса А -1 и А -11, и Е_S = 1,96ּ10⁵ МПа для арматуры класса А – 111

                         R_r – радиус армирования, определяемый по формуле, см:

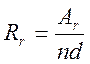
Здесь  - площадь зоны взаимодействия арматура с бетоном;

                                    n – число стержней рабочей арматуры;

                                    d – диаметр арматуры.

Расчет компонентов уравнения проверки на трещиностойкость:

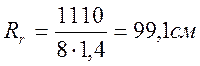
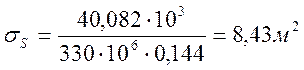
Расчет на трещиностойкость:

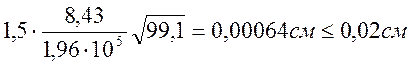
2.  Расчет главных балок полетного строения

2.1. Определение расчетных усилий

Постоянная нагрузка на пролетное строение складывается из собственного веса конструкции и веса мостового полотна.

Нормативная нагрузка на 1 пог. м. главной балки определяется, кН/м:

-  от собственного веса

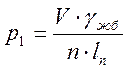
-  от веса мостового полотна с ездой на балласте

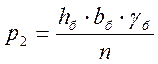
где V и l_п – объем железобетона и полная длина пролетного строения

              n – число главных балок

             h_б – толщина слоя балласта

             b_б – ширина балластного корыта, обычно принимаемая для однопутных мостов 3,6 м.

Получаем 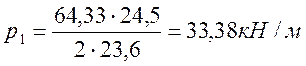 и

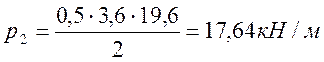
Коэффициенты надежности по нагрузке  для постоянных нагрузок при расчете на прочность принимаются:

-  для собственного веса конструкции

-  для веса мостового полотна с ездой на балласте

Из двух указанных значений коэффициентов надежности по нагрузке принимают то, которое создает наиболее невыгодное суммарное воздействие постоянной и временной нагрузок.

При расчете на прочность нормативная временная нагрузка по схеме СК используется в расчетах в виде

-  эквивалентной нагрузки nК кН/м, соответствующей наиболее тяжелой нагрузки от состава с локомотивом;

-  распределенной нагрузке 9,81 К кН/м, от веса груженных вагонов состава;

-  нагрузки 13,7 кН/м от порожнего подвижного состава.

Однозначные линии влияния и отдельные участки двузначных линий влияния загружаются эквивалентной нагрузкой nК. Нормативная временная вертикальная нагрузка на одну главную балку принимается равной

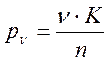
где n - эквивалентная нагрузка класса К=1

      К – класс заданной нагрузки.

	(α = 0,25, λ = 23,6, υ = 13,175 кН/м) (α = 0,5, λ = 23,6, υ = 12,34 кН/м) (α = 0, λ = 23,6, υ = 14,01 кН/м) (α = 0,  λ = 11,8, υ = 16,85 кН/м)

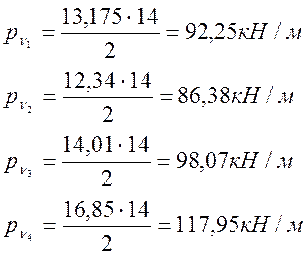
Интенсивность эквивалентной нагрузки n зависит от параметров α и l, определяющих положение вершины и длину загружаемого участка линии влияния. При устройстве пути на балласте значение n принимается соответствующим α = 0,5 независимо от положения вершины линии влияния при l≤10 м.

В общем случае при расчете на прочность загружение линии влияния, состоящих из нескольких участков с разными знаками, производится с целью определения наибольших положительных и отрицательных усилий от временной нагрузки. Для этого одновременно загружаются все участки одного знака, а затем другого. При общей длине загружения L< 80 м каждый участок загружается своей эквивалентной нагрузкой nК, при L ≥ 80 м эквивалентная нагрузка nК ставится на наибольший по площади участок, остальные загружаются нагрузкой