Краткое описание работы вприложении Simulink. Блоки непрерывных моделей, страница 3

Пусть λ_i – простые и вещественные корни характеристического полинома. В этом случае любую матрицу n×n можно привести с помощью некоторого преобразования к диагональной матрице A =diag{l₁,l_2,…,l_n}:

.

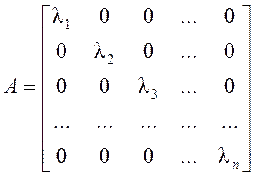Характеристический полином есть определитель характеристической матрицы pE –A =diag{p-l_i}. В случае диагональной матрицы он равен произведению элементов главной диагонали.

Такой базис удобен тем, что в нем уравнения системы распадаются на уравнения n независимых подсистем первого порядка. В развернутой форме уравнения системы имеют вид:

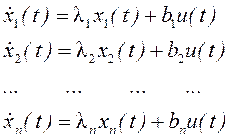
Видно, что здесь x_i(t) не зависит от x_j(t)(i≠j). Вследствие этого упрощается расчет процессов в системе.

Для системы с одним входом и одним выходом  и передаточная функция системы

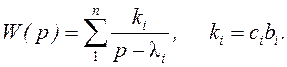
Таким образом, диагональная форма матрицы А соответствует системе, состоящей из параллельно соединенных подсистем первого порядка (апериодических или интегрирующих звеньев).

Для перехода от исходных уравнений состояния к уравнениям в заданной канонической форме необходимо найти такую преобразующую матрицу Т, что для заданных матриц А, В, С получаются уравнения с матрицами , , , имеющими требуемый канонический вид.

При переходе к диагональной форме задается только вид матрицы . Матрицы и  получаются через преобразующую матрицу Т. Поэтому требуется определить матрицу перехода Т такую, что диагональная матрица  Естественно, что характеристические полиномы матриц А и  должны совпадать.

При решении этой задачи обычно используются собственные векторы матриц. Напомним, что собственным вектором некоторой матрицы А, отвечающим собственному значению λ_i называется такой вектор x_i^o, для которого выполняется равенство

Ax_i⁰ = λ_ix_i⁰.

Как известно, собственные векторы определяются с точностью до произвольного ненулевого множителя.

Матрица приведения Т к диагональной канонической форме при простых вещественных собственных числах определяется из выражения

где x_i⁰ – собственные векторы исходной матрицы А.

Пример. Пусть заданы уравнения состояния с матрицами

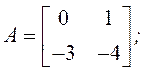
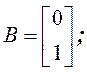
Требуется определить матрицы системы в канонической диагональной форме.

Найдем характеристический полином матрицы А:

A(p) =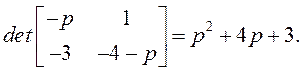

Корни этого полинома (собственные числа матрицы А) равны λ₁=-1, λ₂=-3.

Диагональная форма 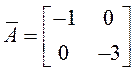. Нетрудно проверить, что собственные числа этой матрицы те же, что и у исходной матрицы.

Вычислим собственные векторы исходной матрицы А.

Для определения собственного вектора, соответствующего собственному числу λ₁=-1 получим следующие уравнения:

x₁ + x₂ = 0,

3x₁ + 3x₂ = 0.

Примем x₁ = 1. Тогда из полученной системы уравнений x₂ = -1.

Следовательно, собственный вектор для  λ₁=-1 будет x₁⁰= [1 -1]^T.

Собственный вектор, соответствующий λ₁=-3 найдем из системы уравнений:

3x₁ + x₂ = 0,

-3x₁ ‑ x₂ = 0.

Выбрав значение x₁ = 1, найдем x₂ = -3. Значит, x₂⁰ = [1 -3]^T.

В результате собственные векторы исходной матрицы А

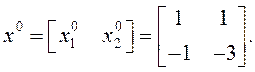
Тогда матрица перехода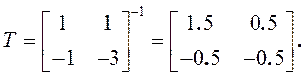  

Обратная матрица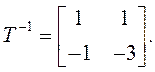

Проверкой можно убедиться, что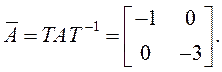  

Матрица  =.

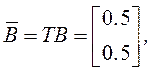
Структурная схема, соответствующая диагональной канонической форме, представлена на рис. 2.3.

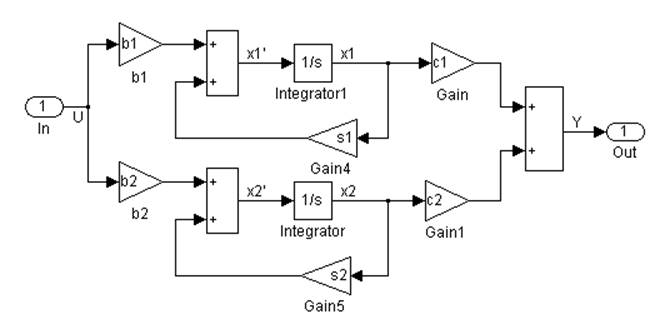
Рис. 2.3. Схема моделирования для диагональной канонической формы

Порядок выполнения этой части работы такой же, как и первой части.

Таблица 2.2

ВАРИАНТЫ ЗАДАНИЙ

для второй части работы

№ варианта	W(s)	№ варианта	W(s)
1		7
2		8
3		9
4		10
5		11
6		12

Контрольные вопросы

1.  Какими способами можно описать динамическую систему?

2.  Как можно перейти от одного способа описания к другому?

3.  Какие известны канонические формы уравнений состояния?

4.  Что такое преобразование подобия?

5.  При каких условиях можно найти матрицу перехода от одной формы уравнений состояния к другой и как ее определить?

6.  Что такое управляемость системы и как установить это свойство?

7.  Что такое наблюдаемость системы и как ее установить?

8.  Однозначен ли переход от уравнений состояния динамической системы к передаточной функции и обратный переход?

9.  Как построить структурную модель системы по уравнениям состояния?

10. Какие функции пакета MatLab выполняют переход от описания системы в форме передаточной функции к описанию в форме уравнений состояния и обратный переход?