Во втором случае система описывается уравнениями состояния, разрешенными относительно первых производных переменных состояния.
Состояние системы определяется векторной переменной x(t)=[x1(t), x2(t), ..., xn(t)], позволяющей однозначно определить выход системы y(t) через ее вход u и начальное состояние x(t)=x(t0).
Линейная система описывается линейными уравнениями состояния и выхода:
![]()
![]() (2)
(2)
где A – матрица объекта размерности n × n, B – матрица управления или входа – n × m, C – матрица выхода – l ×n, D – матрица компенсации – l ×m. В случаях m<n матрица D = 0.
Преобразование уравнений (2) к виду (1) единственно:
W(p)=C(pE-A)-1B+D, где E – единичная матрица.
В большинстве реальных систем m<n, поэтому далее везде будем полагать D = 0.
Переход от уравнений (1) к уравнениям состояния (2) не
является единственным и зависит от базиса пространства состояний. При замене
вектора состояния xдругим
вектором ![]() , связанным со старым
невырожденным преобразованием
, связанным со старым
невырожденным преобразованием
![]() ,
,
где T– матрица преобразования размерности n × n, матричная модель системы принимает вид:
![]()
Здесь матрицы преобразованной модели
![]()
![]()
![]()
При
этом пространство состояний Xзаменяется пространством состояний ![]() той же
размерности. Выходной сигнал системы при переходе к новым переменным состояния
и одинаковых управляющих воздействиях остается неизменным.
той же
размерности. Выходной сигнал системы при переходе к новым переменным состояния
и одинаковых управляющих воздействиях остается неизменным.
Если передаточная функция управляемой системы, имеющей один вход и один выход,
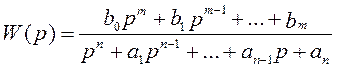 , то можно простым способом получить
уравнения состояния в канонической форме, называемой управляемым каноническим
представлением (УКП). В этой форме матрицы A, B, C имеют вид:
, то можно простым способом получить
уравнения состояния в канонической форме, называемой управляемым каноническим
представлением (УКП). В этой форме матрицы A, B, C имеют вид:
A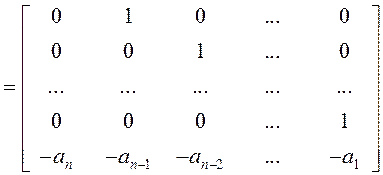 ,
,
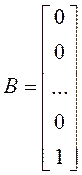 ,
,
C![]() .
.
Здесь А – матрица Фробениуса, в последней строке которой представлены коэффициенты характеристического полинома системы.
Если система не управляема, то представления в форме УКП не существует.
С другой стороны, если матрицы {A, B} управляемой системы заданы, то для получения матрицы А в УКП достаточно вычислить коэффициенты характеристического полинома исходной матрицы.
По уравнениям состояния можно составить структурную модель системы.
Пример. Уравнения состояния и выхода одномерной линейной системы второго порядка имеют вид:
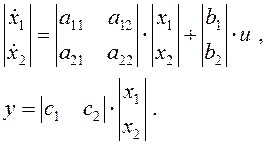
Структурная модель системы, соответствующая этим уравнениям, приведена на рис. 2.1.
Цель работы
Изучение способов математического описания и методов структурного моделирования систем управления.
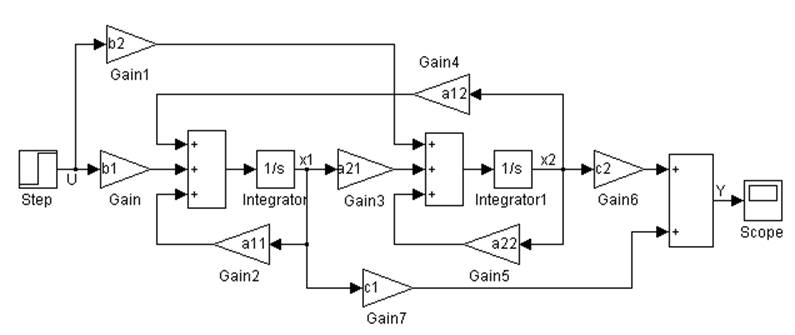
Рис. 2.1. Структурная модель системы 2-го порядка для моделирования в приложении Simulink
Порядок выполнения работы
1. Определить управляемость системы, используя теорему Калмана об управляемости.
2. Вывести передаточную функцию системы, соответствующую заданному варианту работы.
3. Составить матрицы А, В, С для заданной системы в форме УКП.
4. Составить схемы моделирования системы в приложении Simulink: а) исходной системы, заданной в форме передаточной функции, б) структурную схему системы в форме УКП.
Общая схема моделирования приведена на рис. 2.2.
Примечание. Структурную схему системы можно составить согласно примеру, приведенному на рис. 2.1 для системы второго порядка. Затем следует создать подсистему, для чего с помощью ЛКМ выделить часть структурной схемы (от входа U до выхода Y) и выполнить команды Edit\Create subsystem. Далее можно скопировать и сохранить созданную подсистему для использования во второй части работы и в последующих лабораторных работах.
Вторая подсистема содержит блок Transfer Function из библиотеки блоков MatLab.
5. Подать на вход каждой подсистемы единичный ступенчатый сигнал, используя блок Step.
6. В окне параметров блока Scope (Scope’ parameters) установить число входных каналов этого блока (Numberofaxes) равным 2 (для наблюдения процессов в двух окнах). Выбрать параметры моделирования и произвести моделирование. Сравнить полученные переходные процессы и внести их в отчет.
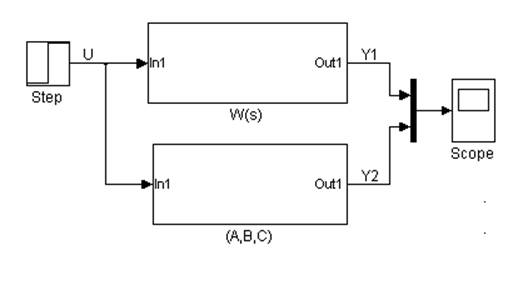
Рис. 2.2. Схема моделирования в приложении Simulink
Таблица 2.1
ВАРИАНТЫ ЗАДАНИЙ
|
№ варианта |
W(s) |
№ варианта |
W(s) |
|
1 |
|
7 |
|
|
2 |
|
8 |
|
|
3 |
|
9 |
|
|
4 |
|
10 |
|
|
5 |
|
11 |
|
|
6 |
|
12 |
|
Отчет по работе должен содержать:
‑ передаточную функцию системы;
‑ уравнения состояния преобразованной системы в краткой и развернутой форме (в соответствии с примером);
‑ графики выходных сигналов;
‑ выводы.
Часть 2
Преобразование уравнений состояния к диагональной форме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.