Частотные характеристики динамических звеньев систем автоматического управления. Экспериментально исследование частотных характеристик типовых динамических звеньев и определение параметров звеньев по этим характеристикам, страница 2

Таблица 3: Третье звено

,

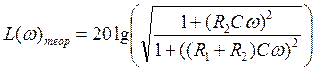
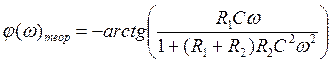
f, Гц	27	120	270	530	800	8000
теоретические данные
L(ω), дБ	0,00	-0,55	-2,24	-5,34	-7,74	-12,26
φ, град	-4,82	-15,01	-26,78	-29,95	-26,78	-4,75
экспериментальные данные
Авх, см	4	4	4	4	4	4
Авых, см	3,8	3,5	2,6	1,9	1,7	1,35
А = Авх/Авых	0,95	0,88	0,65	0,48	0,43	0,34
T, см(период)	6	6	6	6	6	6
τ, см (сдвиг по фазе)	0,1	0,3	0,45	0,5	0,45	0,1
φ, град = (τ/Т)*360	-6	-18	-27	-30	-27	-6
L(ω) = 20lgA	-0,45	-1,16	-3,74	-6,47	-7,43	-9,43
погрешности
∆ L(ω)	1,00	3,09	2,67	2,21	1,96	1,77
∆ φ	0,24	0,20	0,01	0,00	0,01	0,26

Графики теоретических и экспериментальных частотных характеристик отражены в пункте 4.3.

5. Выводы:

В лабораторной работе были исследованы некоторые типовые динамические звенья и их частотные характеристики.

Экспериментально полученные данные и построенные на их основе графики свидетельствуют о том, что реальные и теоретические характеристики очень близки между собой. По характеру графики совпадают. Погрешности между теоретическими и экспериментальными данными могут быть обоснованы наличием погрешности, вносимой осциллографом, и разбросом номиналов элементов.

4.3 Построение теоретических и экспериментальных частотных характеристик звеньев

• Звено №1

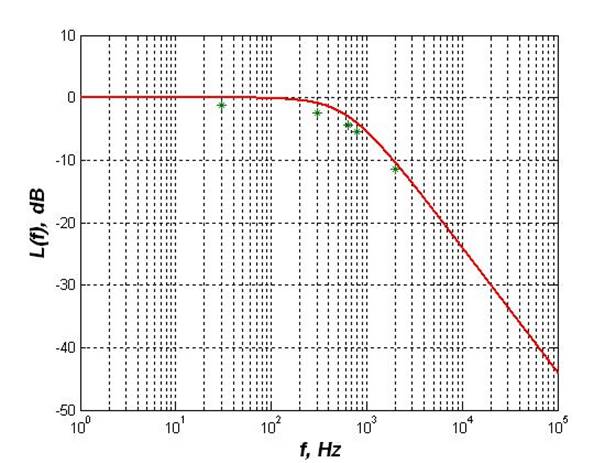
Рис 4.3.1  Логарифмическая частотная характеристика первого звена

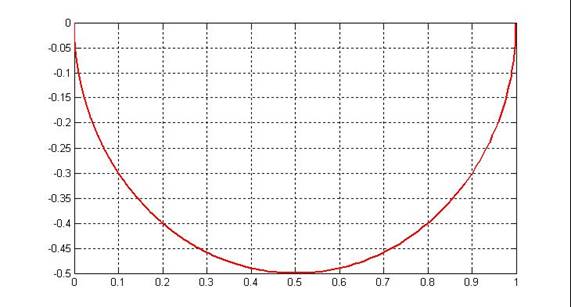
Рис 4.3.2 Амплитудно-фазовая частотная характеристика первого звена на комплексной плоскости

Используя интерполяцию, пользуясь условием: L(f _c) = - 3дБ

Экспериментально определенная частота сопряжения – 670 Гц

Постоянная времени – Т = 0,238 мс

Для апериодического звена коэффициент передачи:

Соответственно, К = 1

• Звено №2

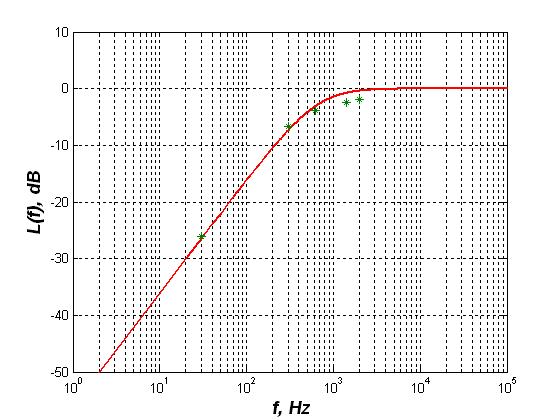
Рис 4.3.3 Логарифмическая частотная характеристика второго звена

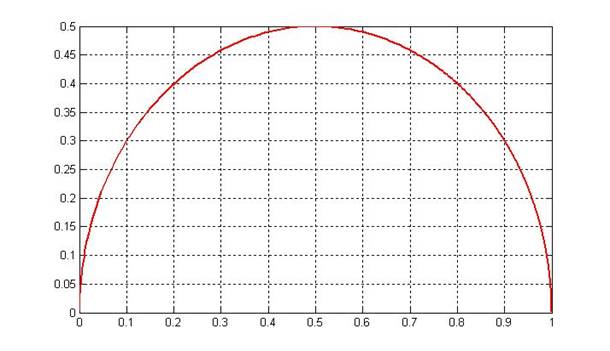
Рис 4.3.4 Амплитудно-фазовая частотная характеристика второго звена на комплексной плоскости

Используя интерполяцию, пользуясь условием: L(f _c) =  3дБ

Экспериментально определенная частота сопряжения – 650 Гц

Постоянная времени – Т = 0,245 мс коэффициент передачи:

Соответственно, К = 1

• Звено №3

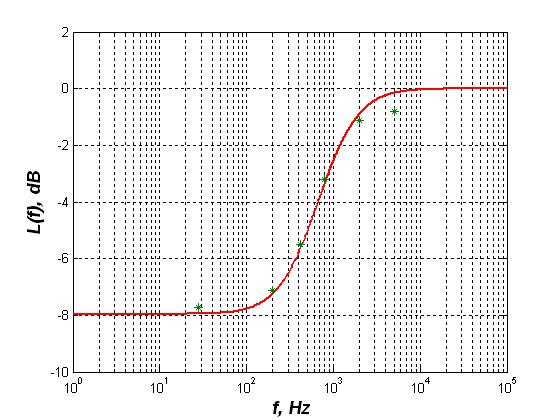
Рис 4.3.5: Логарифмическая частотная характеристика третьего звена

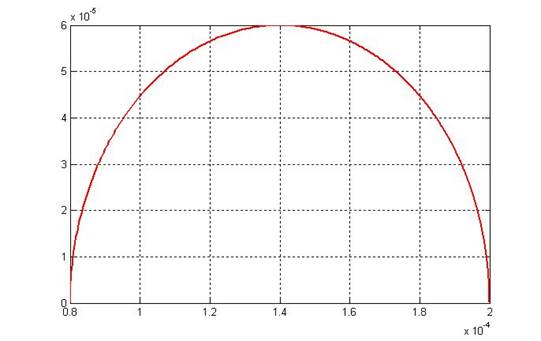
Рис 4.3.6  Амплитудно-фазовая частотная характеристика третьего звена на комплексной плоскости

Используя интерполяцию, пользуясь условием: L(f _c1) = - 6дБ      L(f _c2) = - 2,43дБ

Экспериментально определенные частоты сопряжения  f _c1 = 450 Гц    f _c1 = 1120 Гц

Постоянная времени – Т = 0,338 мс коэффициент передачи:

f  << f _c1, L(f ) = - 8, т.е. К = 0,75

f  >> f _c2 > f _c1,  L(f ) =0, т.е.     К = 0