Управление короткопериодическим движением самолёта. Уравнение объекта. Движение изображающей точки (ИТ) в фазовой плоскости и желаемому аттрактору

СИНЕРГЕТИЧЕСКИЙ СИНТЕЗ РЕГУЛЯТОРОВ АКАР – «АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ АГРЕГИРОВАННЫХ РЕГУЛЯТОРОВ»

Управление короткопериодическим движением самолёта

Уравнение объекта (в пространстве состояний) (*)

x₁ – угол атаки;

x₂ – скорость изменения угла атаки;

u – управление – отклонение угла высоты.

Введём желаемый аттрактор в фазовой плоскости

y (x₁, x₂)=b₁x₁+x₂                                                                                     (1)

Зададим движение изображающей точки (ИТ) в фазовой плоскости и желаемому аттрактору в виде функционального дифференциального уравнения вида:

                                                                                        (2)

Подставив (1) в (2) произведём вычисления

Подставим в уравнение объекта и найдём необходимое управление u₁=a₃u.

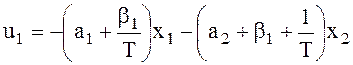
ПД-регулятор, где 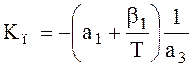, а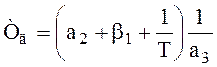

Фазовый портрет системы имеет следующий вид:

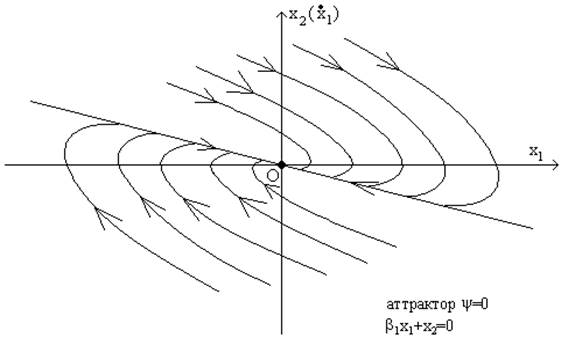
Переходной процесс имеет апериодический характер, причём время движения к аттрактору t»(4-5)T, а по аттрактору в точку «О» t_y»(4-5), общее время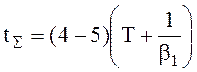

Применение метода обратных задач в динамике

Функциональное управление

 представляем в виде:

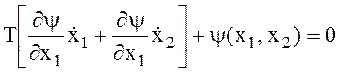
Из этого уравнения находим задаваемое значение

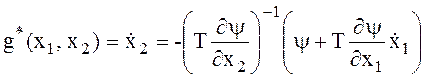
Организуем следящую систему, которая обеспечивает равенство заданного ускорения g^*(x₁, x₂) с ускорением, получаемым из уравнений движения объекта (второе уравнение объекта (*)) и таким образом автоматически вычисляется требуемое значение управления u.

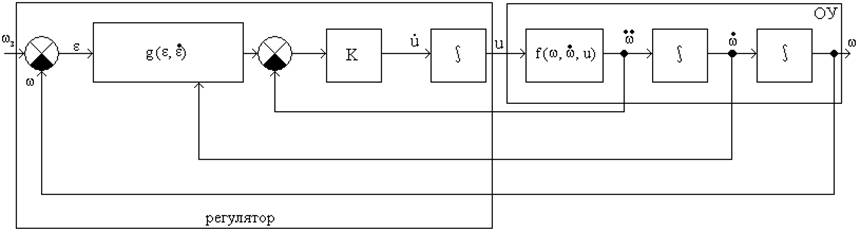
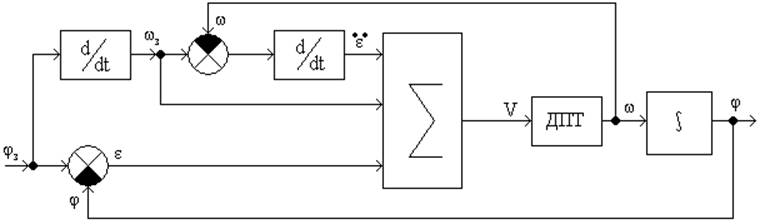
Структурная схема такой системы:

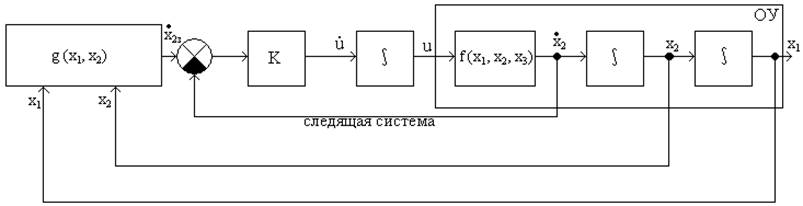
Применительно к рассматриваемому объекту имеем:

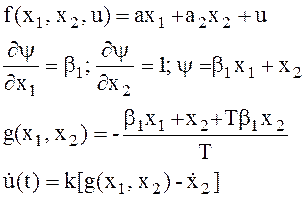
Если аттрактор нелинейная функция, например, y=b₁x₁+b₂x₁³+x₂, получим:

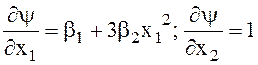
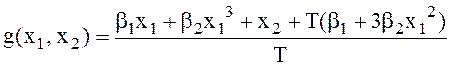
Нелинейный ПД-регулятор:

Синергетический регулятор для управления частотой вращения ДПТ.

Уравнения объекта (ДПТ):

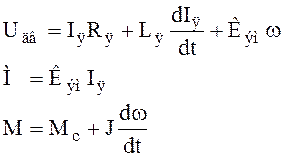
Сделав преобразования, получаем:

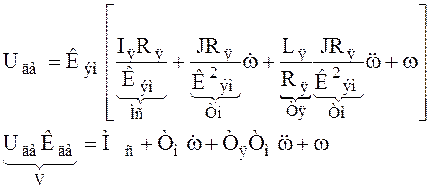
Зададим желаемый аттрактор

Где

И функциональное уравнение

, при

Получим:

, где

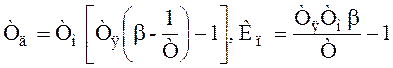
Имеется уравнение объекта (в пространстве состояний):

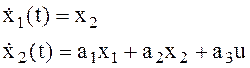
При применении обратных задач динамики получим:

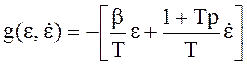
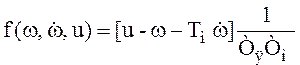
При

Тогда:

Структура регулятора (функциональный ПИД-регулятор):

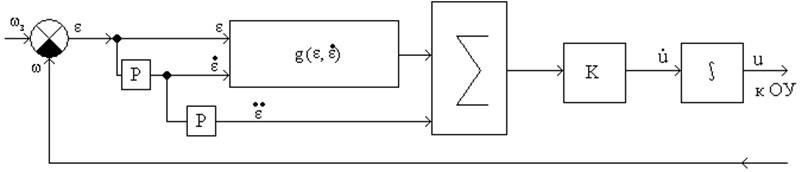
Структура имеет двухканальную систему – «замкнуто-разомкнутую»

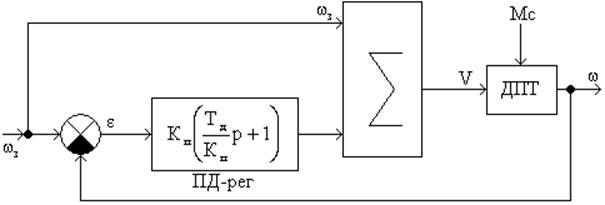
Есть модель для следующих параметров:

Т=0.5Тм, b^-1=0.5Тя;

Тм=100 мс, Тя=10 мс, Тд=0.8Тм;

Кп=3

Уравнение объекта (в пространстве состояний):

Синергетический регулятор для идеальной следящей системы

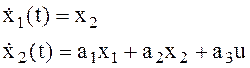
При К_w=10 с^-1, b=50 с^-1, Т=0.08 с

При w_з=const, =0 – система с координацией по скорости.