Исследование систем управления с «Внешнем» запаздыванием. Оценивание влияния запаздывания на качество процессов управления, реализуемого промышленными регуляторами, страница 2

Рис. 3.3.2. Переходная характеристика системы при d_упр = 3, T = 100 мс.

Рис. 3.3.3. Переходная характеристика системы при d_упр = 5, T = 100 мс.

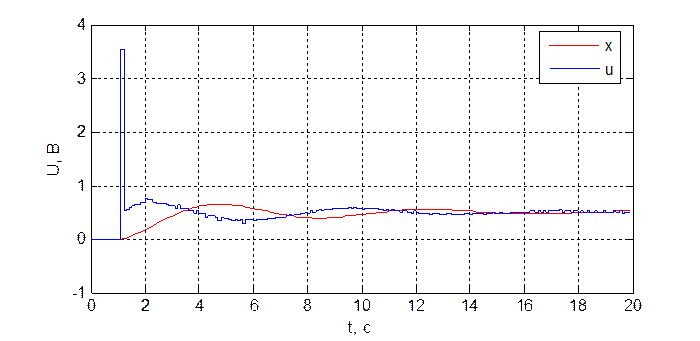
Рис. 3.3.4. Переходная характеристика системы при d_упр = 10, T = 100 мс.

Рис. 3.3.5. Переходная характеристика системы при d_упр = 15, T = 100 мс.

Рис. 3.3.6. Переходная характеристика системы при d_упр = 20, T = 100 мс.

В последнем случае получился расходящийся процесс, из чего можно сделать вывод, что граничное значение задержки по управлению d_упр для данного объекта равно 20 T₀.

3.4. Исследование управления в системе с запаздыванием по наблюдению

В программе delay.exe будем последовательно увеличивать задержку по наблюдению.

В результате будем следить за изменением времени переходного процесса, а также попробуем найти граничное значение задержки, при котором процесс будет сходиться.

На рисунках 3.4.1 – 3.4.6 представлены соответствующие графики.

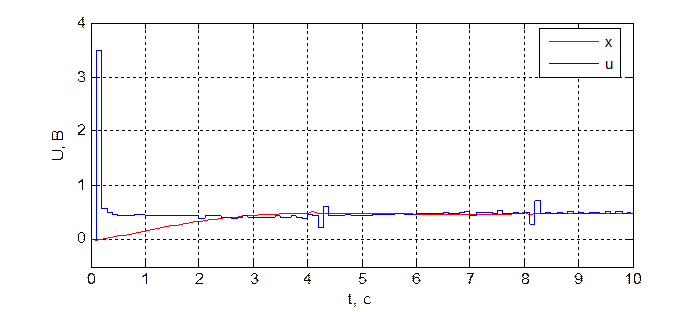
Рис. 3.4.1. Переходная характеристика системы при d_набл = 1, T = 100 мс.

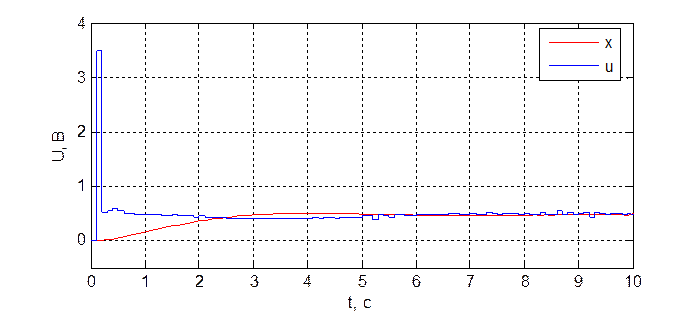
Рис. 3.4.2. Переходная характеристика системы при d_набл = 3, T = 100 мс.

Рис. 3.4.3. Переходная характеристика системы при d_набл = 5, T = 100 мс.

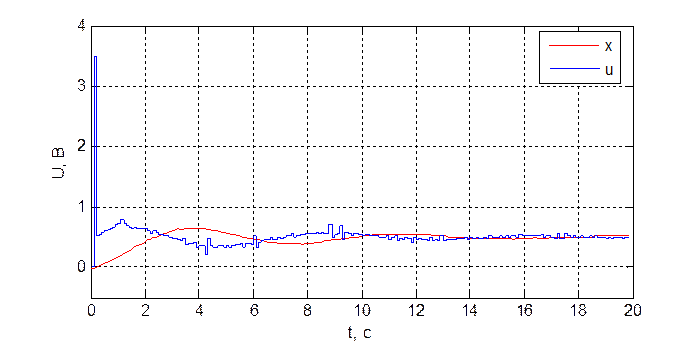
Рис. 3.4.4. Переходная характеристика системы при d_набл = 10, T = 100 мс.

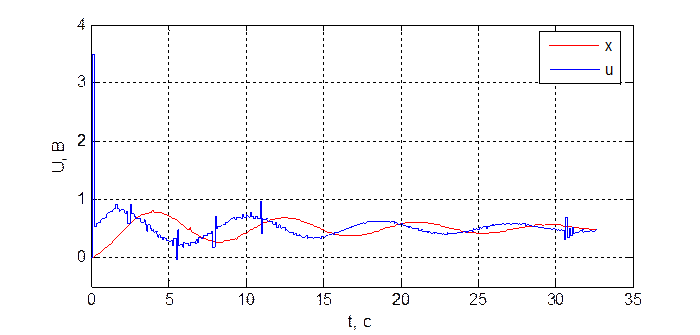
Рис. 3.4.5. Переходная характеристика системы при d_набл = 15, T = 100 мс.

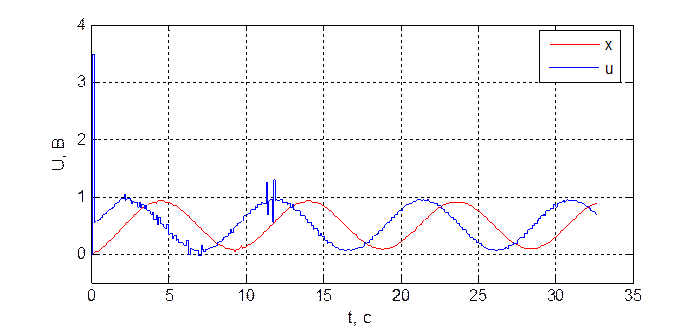
Рис. 3.4.6. Переходная характеристика системы при d_набл = 20, T = 100 мс.

В последнем случае получился расходящийся процесс, из чего можно сделать вывод, что граничное значение задержки по наблюдению d_набл  для данного объекта равно 20 T₀.

3.5. Исследование управления в системе с запаздыванием по управлению и наблюдению

В программе delay.exe будем увеличивать задержку по управлению и по наблюдению.

На рисунках 3.5.1 – 3.5.5 представлены соответствующие графики.

Рис. 3.5.1. Переходная характеристика системы при d_набл = 3, d_упр = 3, T = 100 мс.

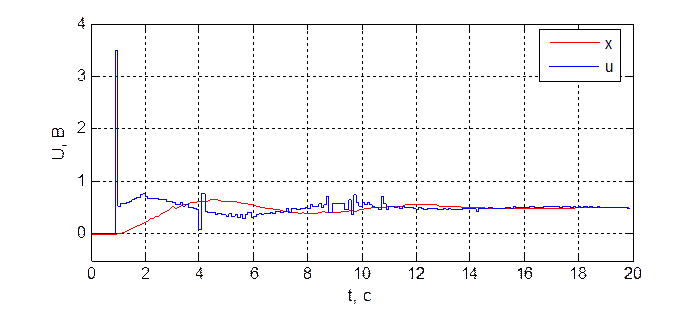
Рис. 3.5.2. Переходная характеристика системы при d_набл = 2, d_упр = 8, T = 100 мс.

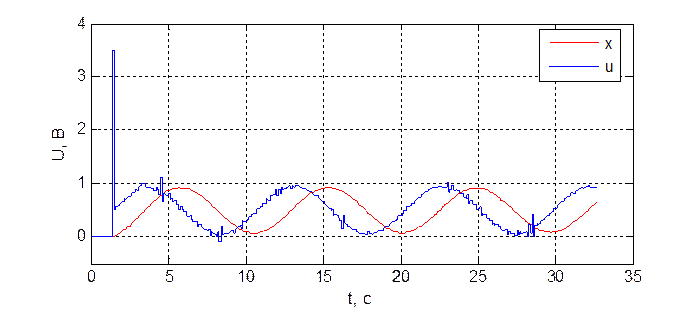
Рис. 3.5.3. Переходная характеристика системы при d_набл = 7, d_упр = 13, T = 100 мс.

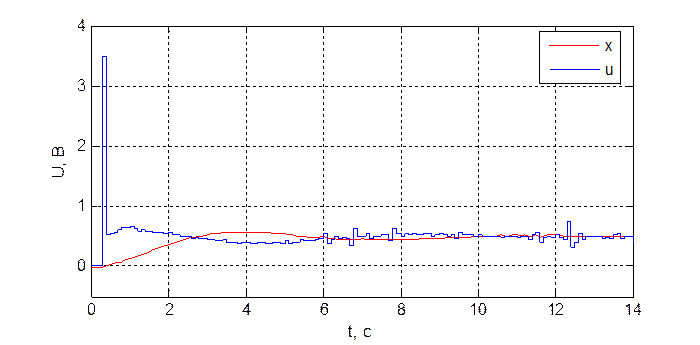
Рис. 3.5.4. Переходная характеристика системы при d_набл = 5, d_упр = 2, T = 100 мс.

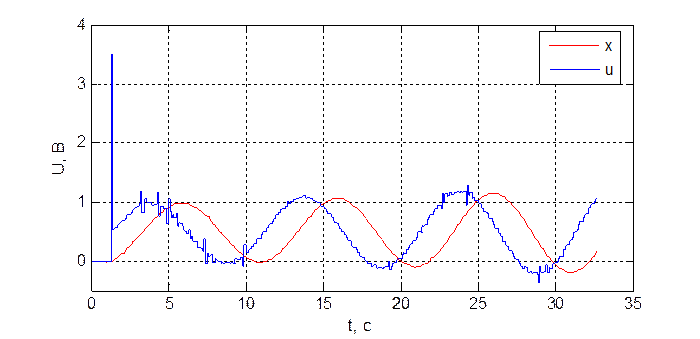
Рис. 3.5.5. Переходная характеристика системы при d_набл = 10, d_упр = 12, T = 100 мс.

В третьем и пятом случае получился расходящийся процесс, из чего можно сделать вывод, что граничная сумма значении задержки по наблюдению d_набл  и задержки по управлению d_упр для данного объекта равно 20 T₀.

3.6. Исследование управления в системе с запаздыванием при граничных значениях задержек.         

Найдем такие Кп, Ки и Кд,  при которых при заданных граничных задержках

d_упр = 10 и d_набл = 10, время переходного процесса будет минимальным.

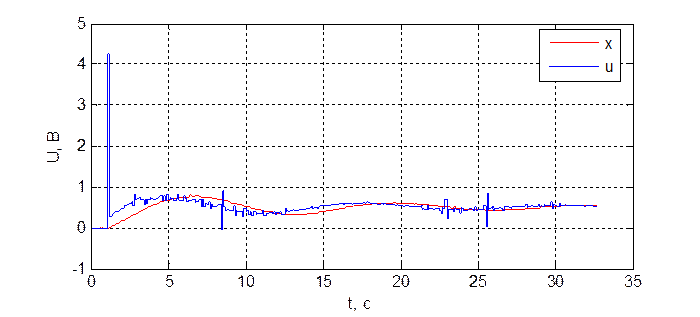
Рис. 3.6.1. Переходная характеристика системы при К_п = 0.5, К_и = 0.5, К_д = 0.8,

x_уст  = 0.5 В, T = 100 мс.

Рис. 3.6.2. Переходная характеристика системы при К_п = 0.3, К_и = 0.4, К_д = 0.8,

x_уст  = 0.5 В, T = 100 мс.

Рис. 3.6.3. Переходная характеристика системы при К_п = 0.3, К_и = 0.2, К_д = 0.8,

x_уст  = 0.5 В, T = 100 мс.

Рис. 3.6.4. Переходная характеристика системы при К_п = 0.4, К_и = 0.2, К_д = 0.6,

x_уст  = 0.5 В, T = 100 мс.

Путем серии экспериментов были найдены оптимальные значения ПИД-регулятора:

К_п=0.3, К_и=0.2, К_Д=0.2.

Время переходного процесса t_пп = 9 сек.

4.         Выводы

В ходе данной работы было проведено исследование влияния запаздывания на качество процессов управления, реализуемого ПИД-регулятором. Выяснили, что увеличение величины запаздывания по управлению и наблюдению негативно сказывается на характере переходного процесса (увеличиваются показатели качества – время переходного процесса, колебательность, перерегулирование). Большие по величине задержки приводят систему в неустойчивое состояние. Можно улучшить качество переходного процесса в системе с запаздыванием путем изменения параметров ПИД-регулятора.