Базовые растровые алгоритмы. Алгоритмы вывода прямой линии. Вычисление текущих координат пикселя

Вычтем из данного равенства равенство для F(M), чтобы определить насколько последнее равенство больше, чем F(M): в результате получится F(M)–2(W–H).

В каждом из случаев к "контрольной величине", т.е. к исходному значению функции, добавляется некоторая константа: 2H или –2(W–H).

Осталось определиться, с чего начинать этот процесс. Мы знаем, что при x=a_x y=a_y. Поэтому первый экземпляр средней точки М=(a_x +1,a_y+1/2) и тогда

F(x,y) = –2W(a_y+1/2–a_y)+2H(a_x+2–a_x) = 2H–W.

Если бы мы предварительно не умножили функцию на 2, то результат был бы H-0,5W, что сделало бы невозможным использование целых значений всех участвующих величин!

Таким образом, перед началом процесса мы полагаем F=2H–W, x=a_x, y=a_y. Затем на каждом шаге делаем следующее:

-  присваиваем пикселю (x,y) нужное значение цвета.

-  Увеличиваем x на 1; если F<0, то добавляем к F величину 2H; в противном случае увеличиваем y на 1 и добавляем к F величину -2(W-H)=2(H-W).

Все вышеизложенное и определяет алгоритм Брезенхема для данного частного случая. Поскольку в этом алгоритме предусмотрена повторная инициализация для каждой новой прямой, то он является повторяемым: повторное рисование какой-либо прямой другим цветом полностью замещает первую прямую: например, рисование цветом фона целиком удаляет ранее нарисованную прямую.

Алгоритм Брезенхема предельно прост, в его внутреннем цикле содержатся только несколько операций сравнения и сложения. Для достижения максимальной скорости его легко реализовать на языке ассемблера. Этот алгоритм часто используется аппаратно в графических устройствах специального назначения, где обеспечивается еще большая его скорость.

Пример: Изменение функции F

Пусть а()=(4,1); b()= (16,4). Тогда W=12 H=3. Поскольку наклон данной прямой линии равен 0,25, мы ожидаем, что значение y будет увеличиваться только примерно на каждом 4-ом шаге по х. Начальное значение функции F отрицательно F=2H–W=6–12=(–6).

При каждом увеличении х мы делаем одно из двух: если значение функции F отрицательно, то добавляем 2H=6; в противном случае вычитаем из нее 18 и увеличиваем y.

В результате получаем следующую последовательность значений:

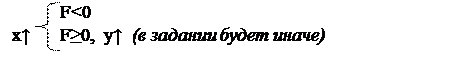
Отмена ограничений на алгоритм Брезенхема

Алгоритм Брезенхема применим только в частном случае, когда a_x<b_x  и наклон прямой линии находится в диапазоне от 0 до 1. Все остальные случаи легко охватываются, если добавить код, обрабатывающий каждый случай более общего вида.

Получение той же прямой при a_x >b_x. Алгоритм средней точки определяет нахождение пикселя по нужную сторону от средней точки, выбирая на каждом шаге один из двух вариантов. Тогда нам нужно изменить код в подпрограмме так, чтобы он выполнял алгоритм средней точки для данного случая. Следует отметить, что в базовом алгоритме случай F=0 рассматривается вместе со случаем F>0 (где y увеличивается). При изменении направления прямой  случай F=0 необходимо рассматривать вместе со случаем F<0 (где y уменьшается).

Предпочтительнее использовать обратный алгоритм (соответствует большинству приложений для работы с растровой графикой):

1) если y:

F£0

F>0 Þ y

2) если y¯:

F<0

F³0 Þ y¯

Существует и альтернативный подход: если обнаружилось, что a_x >b_x, то a_x и b_x  необходимо поменять местами, после чего проделываются все шаги, предусмотренные в базовом алгоритме. На деле при таком подходе не происходит "рисования справа налево", а вместо этого конечные точки переопределяются так, что такого рисования и не требуется. Такая технология, однако, не очень удобна в тех наблюдениях, когда требуется использовать данный алгоритм для рисования соединенных между собой отрезков прямых, как при визуализации ломаной линии. Перестановка концевых точек нарушила бы естественный порядок, в котором рисуются отрезки ломаной, а этот порядок может оказаться важным, если эти отрезки рисуются штриховыми или пунктирным линиями.

Прямые с наклоном больше 1

В этом случае x и y просто меняются местами, делаются шаги по y от a_y  до b_y и производится такая же проверка ситуаций, когда нужно увеличивать (более медленно изменяющееся) x.

Прямые с отрицательным наклоном

Если этот наклон лежит в диапазоне от 0 до –1, то H автоматически приобретает нужный знак. Мы двигаемся по x с использованием тех же тестов, однако вместо увеличения зависимой переменной уменьшаем ее. Если же наклон меньше –1 (более отрицательный), то заменяем