Координатный метод. Преобразование координат. Функция пересчета i-ой координаты, аргументы – координаты в системе

КООРДИНАТНЫЙ МЕТОД

Координатный метод был введен в XVII веке французскими математиками  Р.Декартом и П.Ферма. На этом методе основывается аналитическая геометрия, которую можно считать фундаментом компьютерной графики. В современной компьютерной графике используется широко координатный метод. Этому есть несколько причин:

-  каждая точка на экране (или на бумаге при печати на принтере) задается координатами – например, пиксельными.

-  координаты используются для описания объектов, которые будут отображаться как пространственные. Даже, когда отображается нечто, не имеющее привязки в пространстве (например, случайные цветовые пятна в каком-то видеоэффекте), то и здесь используются координаты для учета взаиморасположения отдельных элементов.

-  при выполнении многих промежуточных действий отображения используют разные системы координат и преобразования из одной системы в другую.

1. Преобразование координат

Сначала рассмотрим общие вопросы преобразования координат. Пусть задана n-мерная система координат в базисе (k₁, k₂, …, k_n), описывающая положение точки в пространстве с помощью числовых значений k_i. В компьютерной графике чаще всего используется  двумерная (n=2) и трехмерная (n=3) системы координат.

Если задать другую, N-мерную систему координат в базисе (m₁, m₂, …, m_N), и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

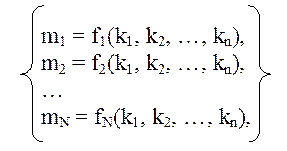
где f_i – функция пересчета i-ой координаты, аргументы –координаты в системе k_i.

Можно поставить и обратную задачу – по известным координатам (m₁, m₂, …, m_N) определить координаты (k₁, k₂, …, k_n). Решение обратной задачи запишем так:

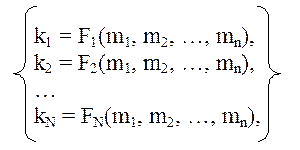
где F_i – функции обратного преобразования.

В случае, когда размерности систем координат не совпадают (n¹N), осуществить однозначное преобразование координат зачастую не удается. Например, по двумерным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты воображаемых объектов.

Если размерности систем совпадают (n=N), то также возможны случаи, когда нельзя однозначно решить прямую или обратную задачи.

Преобразование координат классифицируют:

-  по системам координат – например, преобразование из полярной системы в прямоугольную;

-  по виду функций преобразования f_i.

По виду функций преобразования различают линейные и нелинейные преобразования. Если при всех i = 1, 2, …, N функции f_i – линейные относительно аргументов (k₁, k₂, …, k_n), то есть

f_i=a_i1k₁+ a_i2k₂+ … +a_in k _n+ a_i,n+1, где a_ij – константы, то такие преобразования называются линейными, а при n=N – аффинными.

Если хотя бы для одного i функция f_i – нелинейная относительно (k₁, k₂, …, k_n), тогда преобразование координат в целом нелинейно.

Например, преобразование

X=3x+5y

Y=4xy+10y

нелинейное, т.к. в выражении для Y присутствует xy.

Линейные преобразования наглядно записываются в матричной форме:

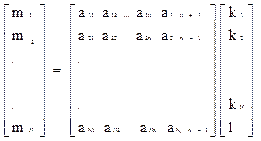
Здесь матрица коэффициентов (a_ij) умножается на матрицу столбец (k_i) и в результате получается матрица столбец (m_i).

Таким образом, аффинное преобразование имеет следующие свойства:

-  Отображает n-мерный объект в n-мерный – точку в точку, линию в линию, поверхность в поверхность;

-  Сохраняет параллельность линий и плоскостей;

-  Сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.

Эти свойства позволяют строить прообразы полигонов на плоскости и полиэдров в пространстве по конечному набору m точек их вершин, далее вершины соединяются прямыми линиями (ребрами) в нужном порядке. Система вершин и ребер составляет каркасную (проволочную ) модель полигона и полиэдра. Для получения объемной модели определяются и закрашиваются видимые грани.

Для упрощения и унификации записи геометрических преобразований