Информатика и выч. техника \ Идентификация и диагностика систем управления

Моделирование системы диагностирования, построенной с использованием структурных инвариантов. Построение структурных инвариантов

Страницы работы

25 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ

по лабораторной работе №3

Дисциплина: идентификация и диагностика систем управления

Тема: Моделирование системы диагностирования, построенной с использованием структурных инвариантов

Вариант: 22

Выполнил студент гр. 5081/11 Б

Проверил:

Санкт-Петербург 2010

1. Задание

Исследовать систему диагностирования, построенную с помощью структурных инвариантов. Структурно система состоит из трех информационных каналов (ИК), дублирующих друг друга. Сигнал в ИК представляет собой последовательность независимых случайных величин, распределенных нормально с нулевым математическим ожиданием и единичной дисперсией.

Программа работы:

1. Осуществить построение структурных инвариантов, заданных в следующем виде:

1). разность одноименных параметров различных ИК;

2). разность параметров отдельных каналов и следующей статистики: среднее арифметическое.

2. Провести моделирование системы в режиме нормального функционирования, построить графики сигналов в ИК.

3. Определить следующие типы дефектов:

1). Сдвиг (изменение среднего уровня систематической погрешности) в одном из каналов;

2). Изменение уровня шумов (увеличение дисперсии) в одном из каналов.

Ввести три уровня для каждого дефекта: малый, средний и большой; определить величины дефектов для каждого уровня.

Провести моделирование системы в режиме функционирования с дефектом. Построить графики сигналов в ИК.

4. Сформулировать выводы о проделанной работе, оформить отчет.

1. Выполнение работы

1.1. Построение системы, инвариант – разность одноименных параметров различных ИК.

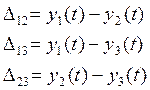
Оценка инвариантов - изменение математического ожидания и дисперсии.

1.m

clear all

count = 5000; % число измерений

M = 0; % значение мат. ожидания

D = 1; % значение дисперсии

Dfm = 2500; % момент возникновения неисправности

T = 1:count;

for i=1:count

if (i < Dfm)

base1(i) = normrnd(0,1);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

else

base1(i) = normrnd(M,D);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

end

% Инвариант

delta12(i) = base1(i) - base2(i);

delta13(i) = base1(i) - base3(i);

delta23(i) = base2(i) - base3(i);

% Оценка инварианта

mu1(i) = mean(delta12);

mu2(i) = mean(delta13);

mu3(i) = mean(delta23);

d1(i) = std(delta12);

d2(i) = std(delta13);

d3(i) = std(delta23);

end

figure

subplot(3,1,1);

plot(T,base1,'b');

ylabel('y1');

subplot(3,1,2);

plot(T,base2,'r');

ylabel('y2');

subplot(3,1,3);

plot(T,base3,'g');

xlabel('t');

ylabel('y3');

figure

% Оценка мат. ожидания

subplot(2,1,1);

plot(T,mu1,'b',T,mu2,'r',T,mu3,'g');

ylabel('M');

% Оценка дисперсии

subplot(2,1,2);

plot(T,d1,'b',T,d2,'r',T,d3,'g');

xlabel('t');

ylabel('D');

Малый сдвиг (M = 0.3, D = 1):

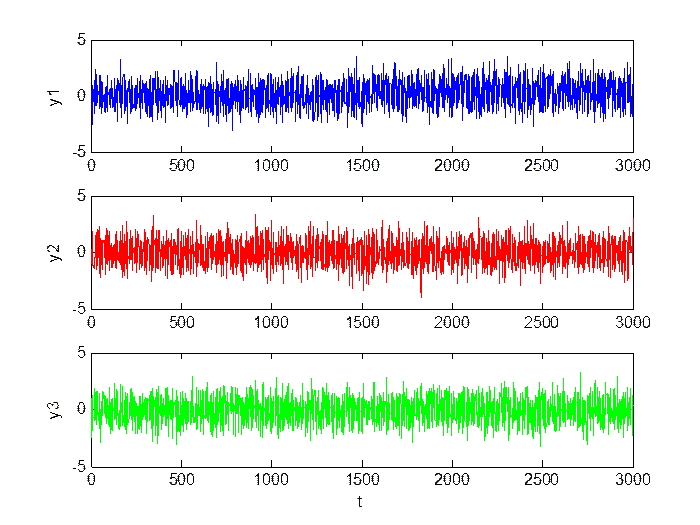
Рис.1.1. Сигнал в каналах.

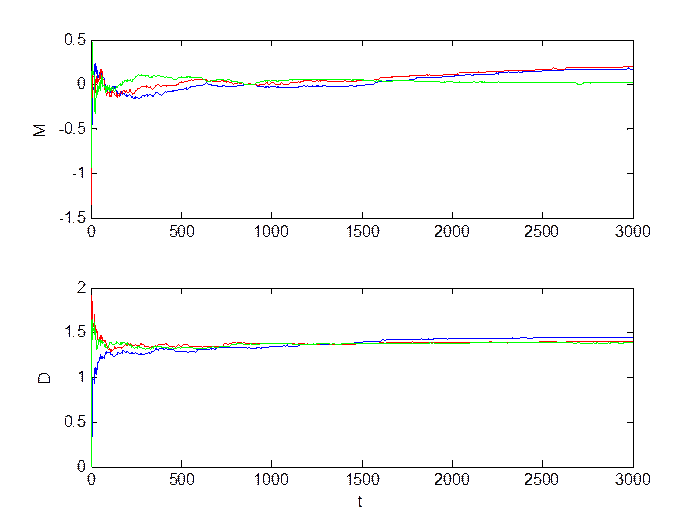
Рис.1.2. Оценка инвариантов.

Средний сдвиг (M = 0.8, D = 1):

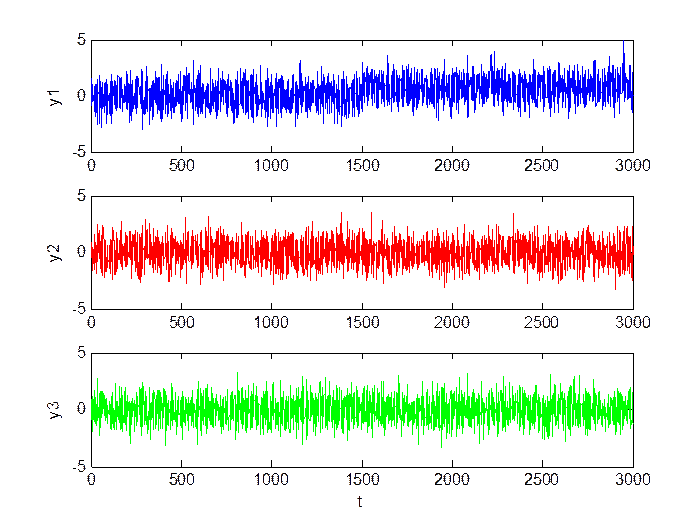
Рис.1.3. Сигнал в каналах.

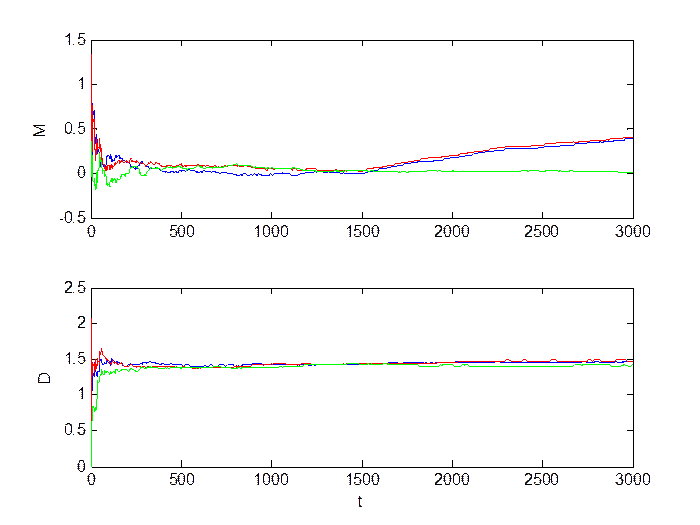
Рис.1.4. Оценка инвариантов.

Большой сдвиг (M = 3, D = 1):

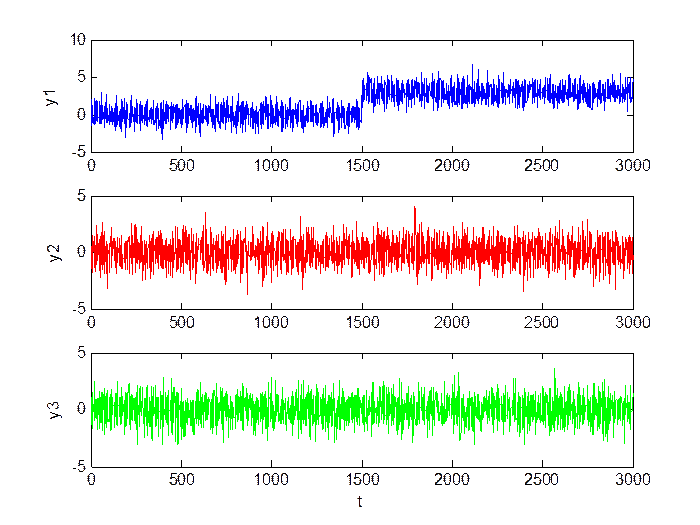
Рис.1.5. Сигнал в каналах.

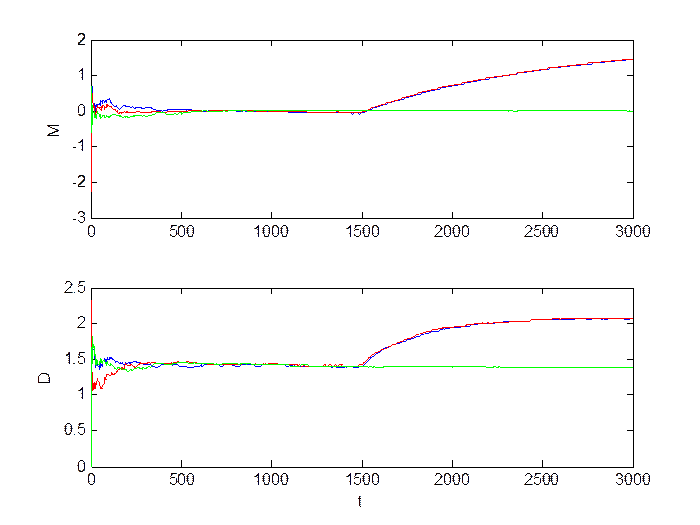
Рис.1.6. Оценка инвариантов.

Малое изменение уровня шумов (M = 0, D = 1.5):

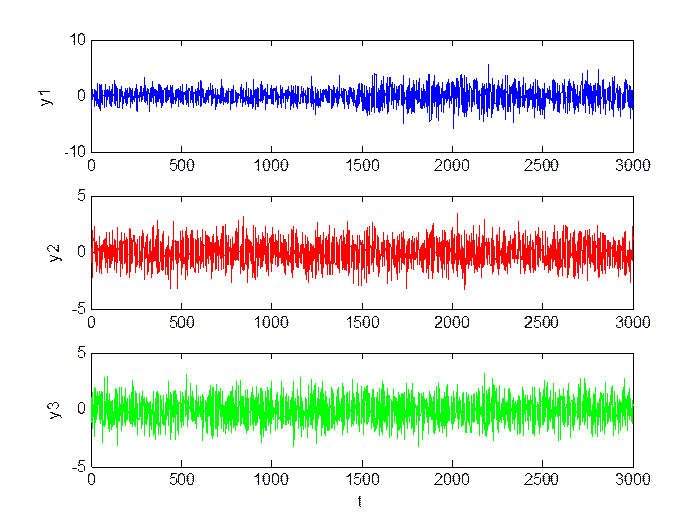
Рис.1.7. Сигнал в каналах.

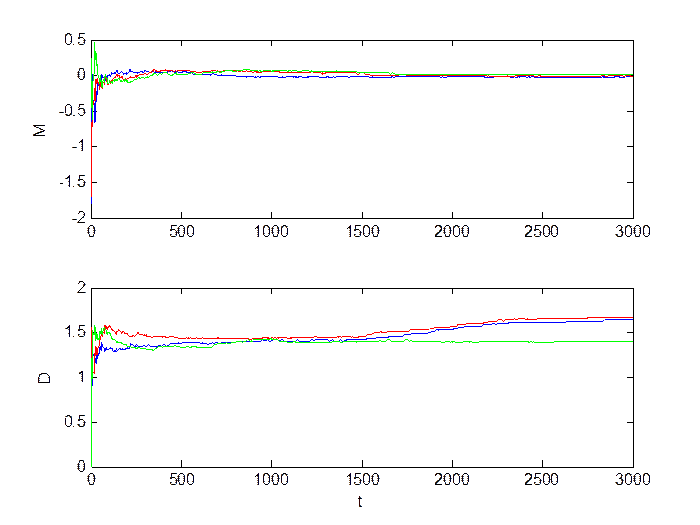
Рис.1.8. Оценка инвариантов.

Среднее изменение уровня шумов (M = 0, D = 2.5):

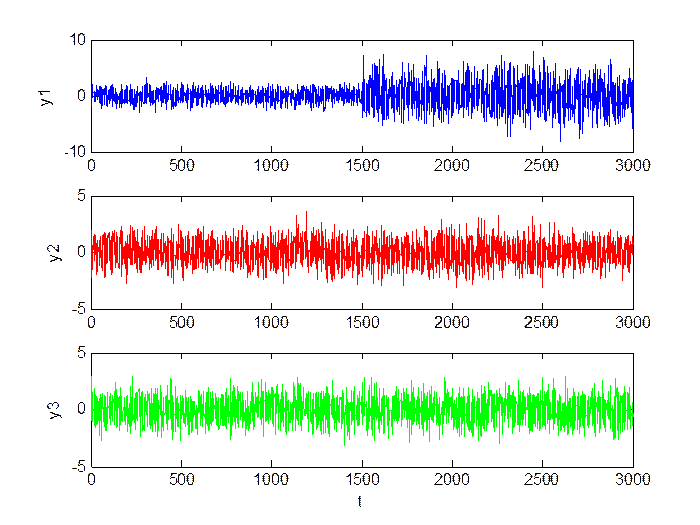
Рис.1.9. Сигнал в каналах.

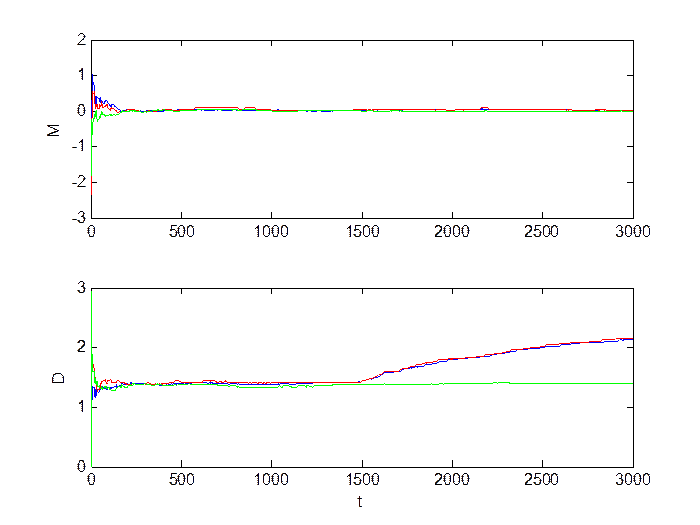
Рис.1.10. Оценка инвариантов.

Большое изменение уровня шумов (M = 0, D = 5):

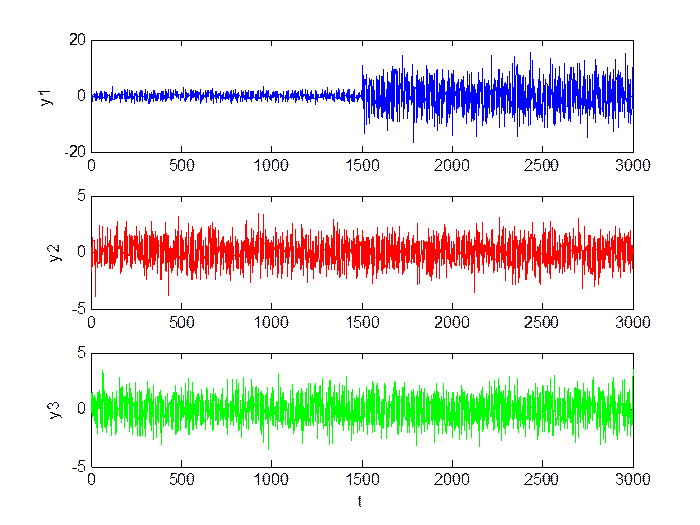
Рис.1.11. Сигнал в каналах.

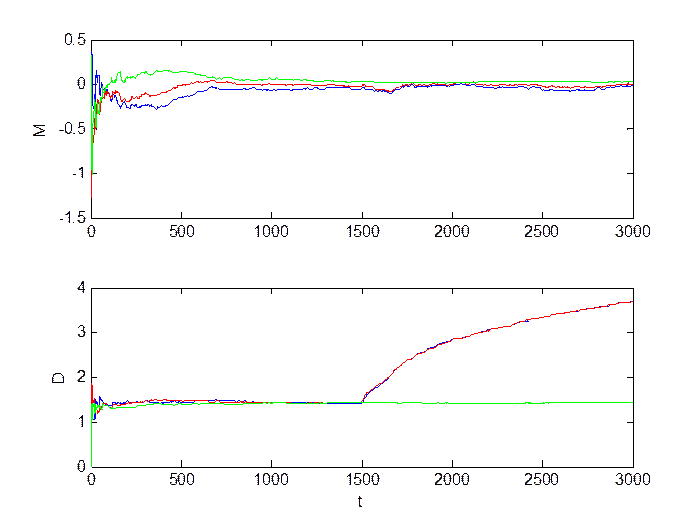
Рис.1.12. Оценка инвариантов.

1.2. Построение системы, инвариант – разность между параметрами ИК и средним арифметическим.

2.m

clear all

count = 5000; % число измерений

M = 0; % значение мат. ожидания

D = 1; % значение дисперсии

Dfm = 2500; % момент возникновения неисправности

T = 1:count;

for i=1:count

if (i < Dfm)

base1(i) = normrnd(0,1);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

else

base1(i) = normrnd(M,D);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

end

% Инвариант

delta1(i) = base1(i) - 1/3*(base1(i)+base2(i)+base3(i));

delta2(i) = base2(i) - 1/3*(base1(i)+base2(i)+base3(i));

delta3(i) = base3(i) - 1/3*(base1(i)+base2(i)+base3(i));

% Оценка инварианта

mu1(i) = mean(delta1);

mu2(i) = mean(delta2);

mu3(i) = mean(delta3);

d1(i) = std(delta1);

d2(i) = std(delta2);

d3(i) = std(delta3);

end

figure

subplot(3,1,1);

plot(T,base1,'b');

ylabel('y1');

subplot(3,1,2);

plot(T,base2,'r');

ylabel('y2');

subplot(3,1,3);

plot(T,base3,'g');

xlabel('t');

ylabel('y3');

figure

% Оценка мат. ожидания

subplot(2,1,1);

plot(T,mu1,'b',T,mu2,'r',T,mu3,'g');

ylabel('M');

% Оценка дисперсии

subplot(2,1,2);

plot(T,d1,'b',T,d2,'r',T,d3,'g');

xlabel('t');

ylabel('D');

Малый сдвиг (M = 0.3, D = 1):

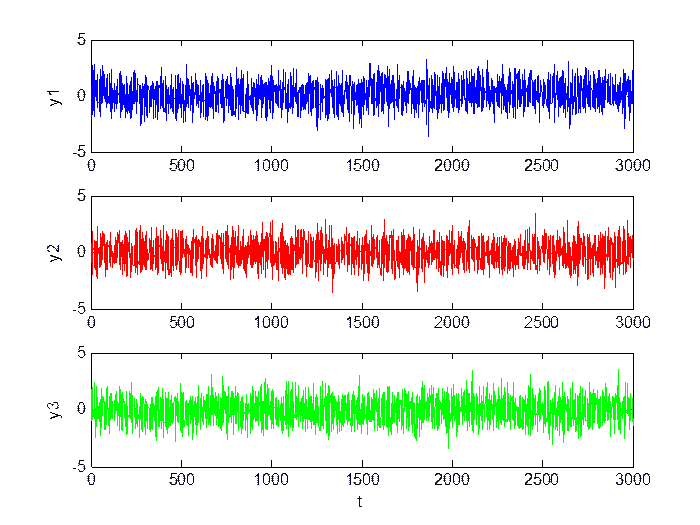
Рис.2.1. Сигнал в каналах.

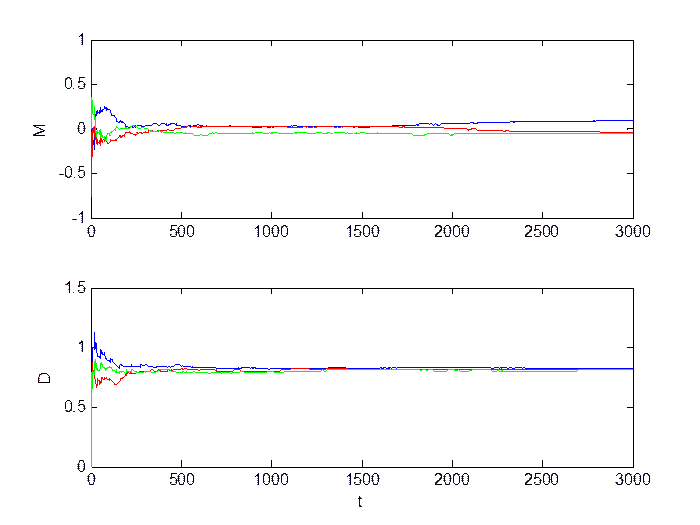
Рис.2.2. Оценка инвариантов.

Средний сдвиг (M = 0.8, D = 1):

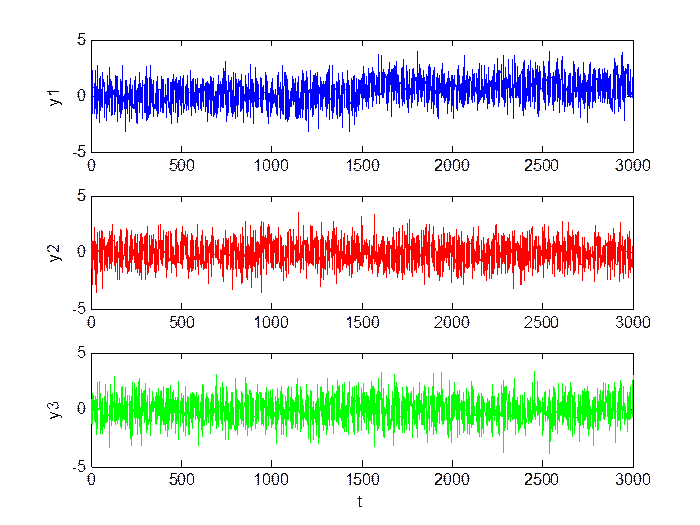
Рис.2.3. Сигнал в каналах.

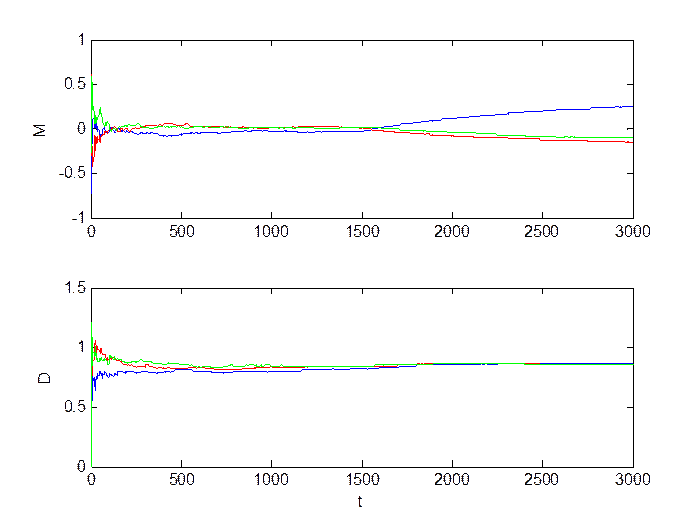
Рис.2.4. Оценка инвариантов.

Большой сдвиг (M = 3, D = 1):

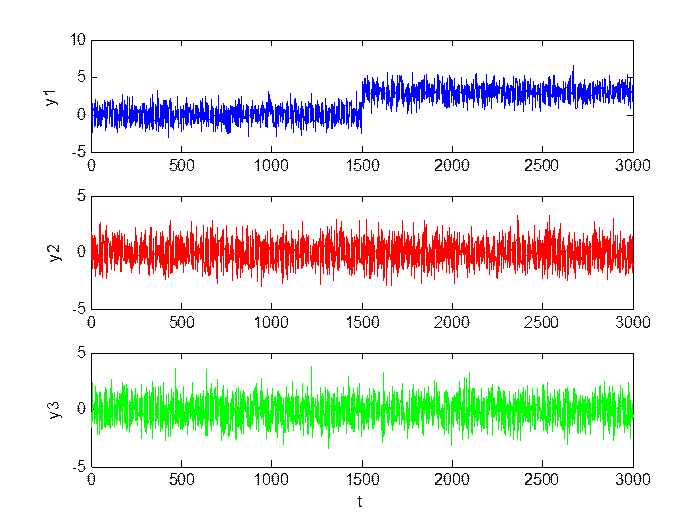
Рис.2.5. Сигнал в каналах.

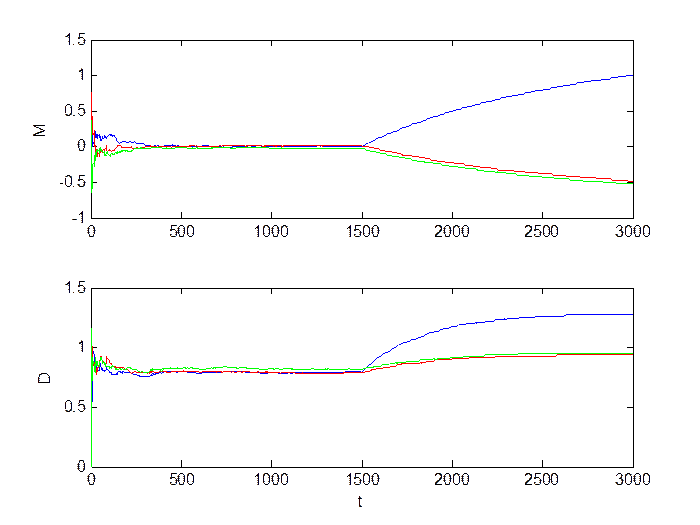
Рис.2.6. Оценка инвариантов.

Малое изменение уровня шумов (M = 0, D = 1.5):

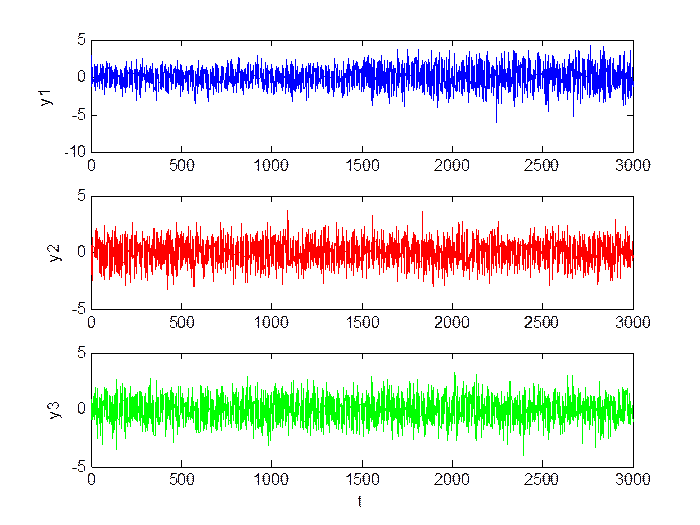
Рис.2.7. Сигнал в каналах.

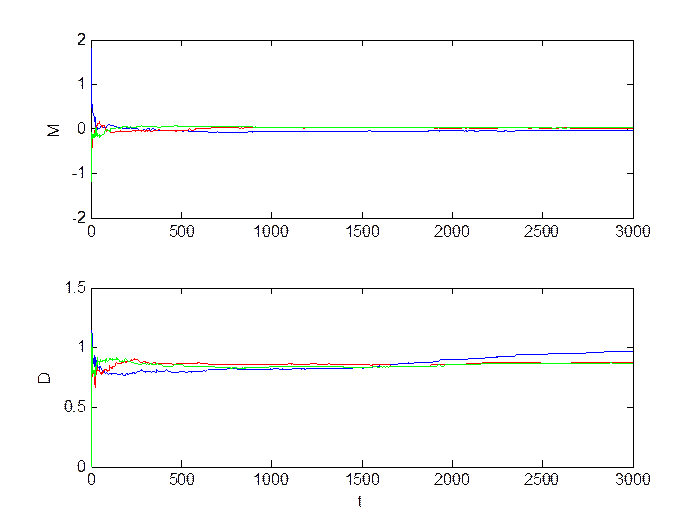
Рис.2.8. Оценка инвариантов.

Среднее изменение уровня шумов (M = 0, D = 2.5):

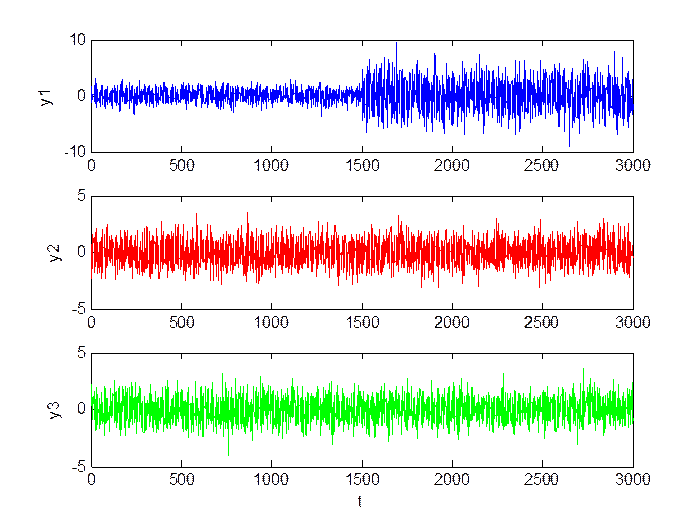
Рис.2.9. Сигнал в каналах.

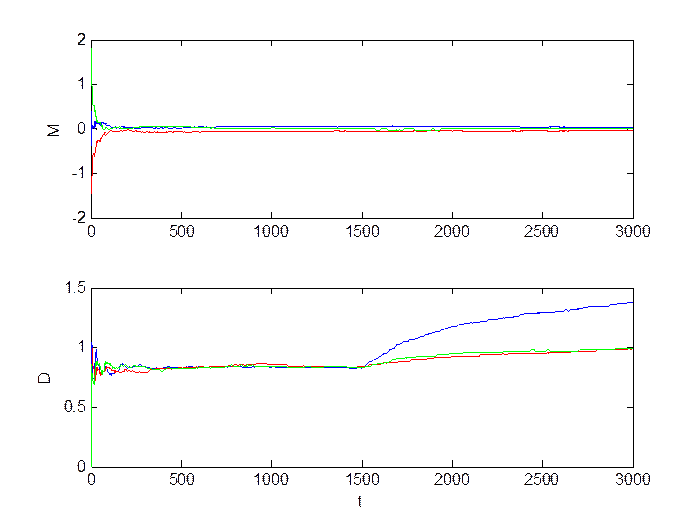
Рис.2.10. Оценка инвариантов.

Большое изменение уровня шумов (M = 0, D = 5):

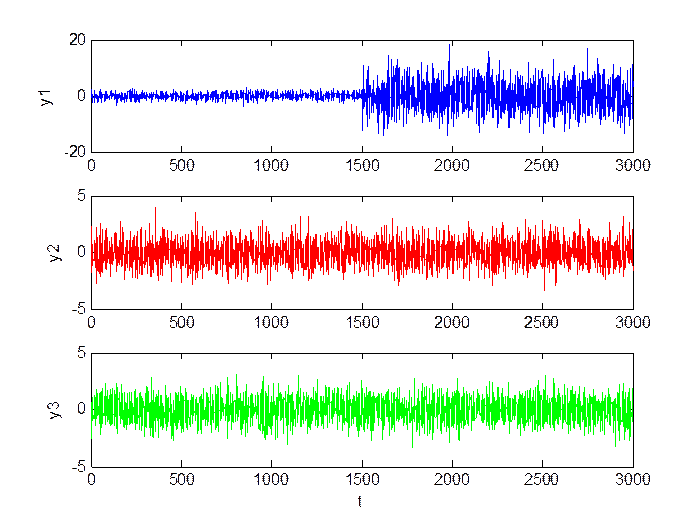
Рис.2.11. Сигнал в каналах.

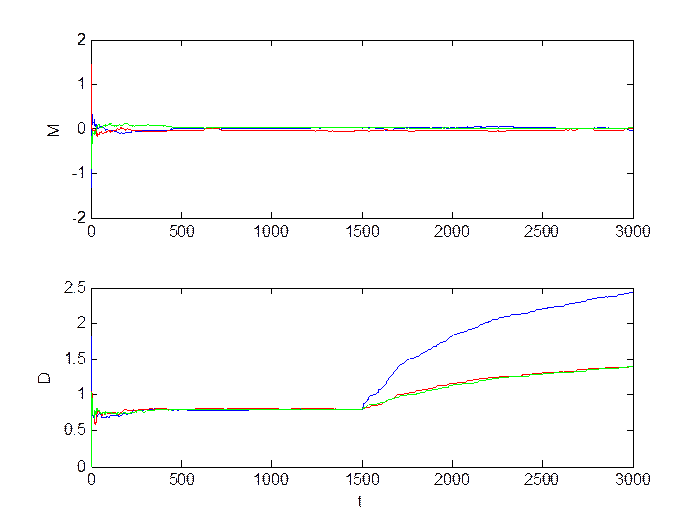
Рис.2.12. Оценка инвариантов.

1.3. Построение системы, инвариант – разность между параметрами ИК и порядковым средним.

3.m

clear all

count = 3000; % число измерений

M = 0; % значение мат. ожидания

D = 5; % значение дисперсии

Dfm = 1500; % момент возникновения неисправности

T = 1:count;

for i=1:count

if (i < Dfm)

base1(i) = normrnd(0,1);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

else

base1(i) = normrnd(M,D);

base2(i) = normrnd(0,1);

base3(i) = normrnd(0,1);

end

% Инвариант

delta1(i) = base1(i) - median(cat(2,base1(i), base2(i), base3(i)));

delta2(i) = base2(i) - median(cat(2,base1(i), base2(i), base3(i)));

delta3(i) = base3(i) - median(cat(2,base1(i), base2(i), base3(i)));

% Оценка инварианта

mu1(i) = mean(delta1);

mu2(i) = mean(delta2);

mu3(i) = mean(delta3);

d1(i) = std(delta1);

d2(i) = std(delta2);

d3(i) = std(delta3);

end

figure

subplot(3,1,1);

plot(T,base1,'b');

ylabel('y1');

subplot(3,1,2);

plot(T,base2,'r');

ylabel('y2');

subplot(3,1,3);

plot(T,base3,'g');

xlabel('t');

ylabel('y3');

figure

% Оценка мат. ожидания

subplot(2,1,1);

plot(T,mu1,'b',T,mu2,'r',T,mu3,'g');

ylabel('M');

% Оценка дисперсии

subplot(2,1,2);

plot(T,d1,'b',T,d2,'r',T,d3,'g');

xlabel('t');

ylabel('D');

Малый сдвиг (M = 0.3, D = 1):

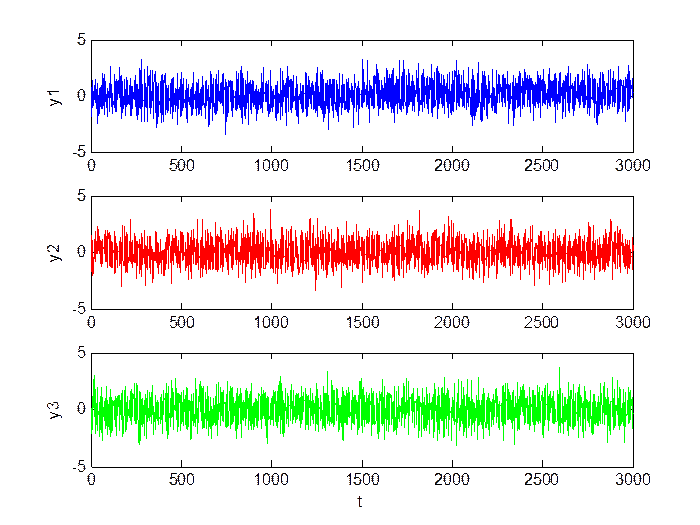
Рис.3.1. Сигнал в каналах.

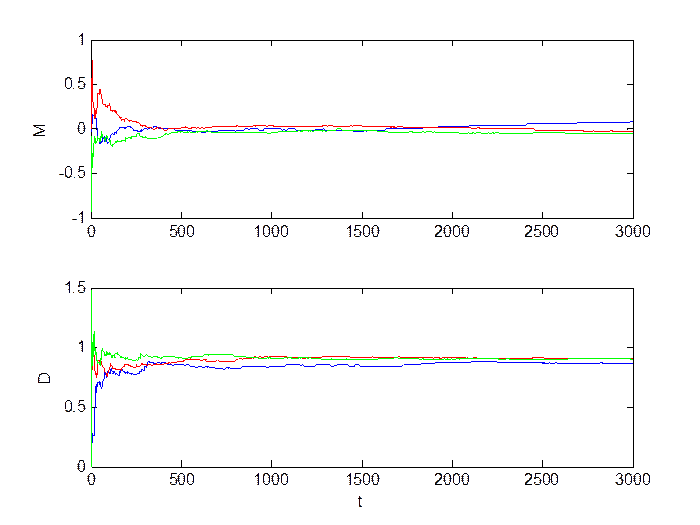
Рис.3.2. Оценка инвариантов.

Средний сдвиг (M = 0.8, D = 1):

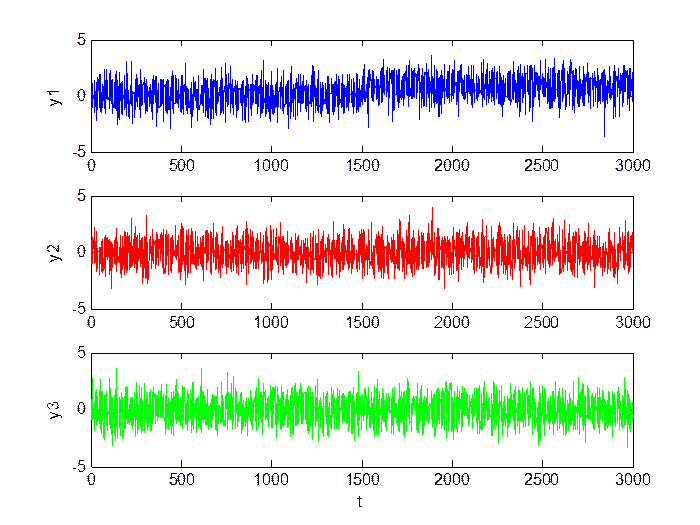
Рис.3.3. Сигнал в каналах.

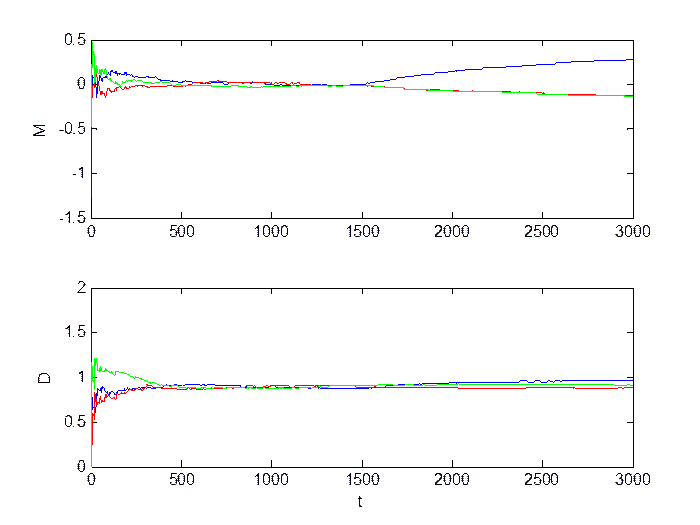
Рис.3.4. Оценка инвариантов.

Большой сдвиг (M = 3, D = 1):

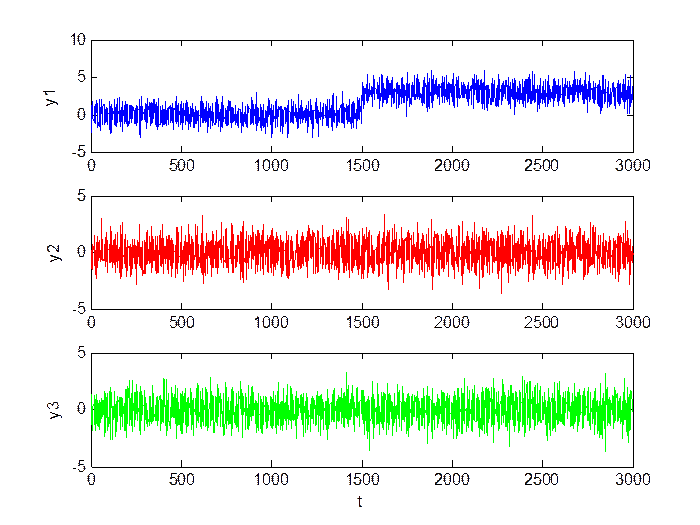
Рис.3.5. Сигнал в каналах.

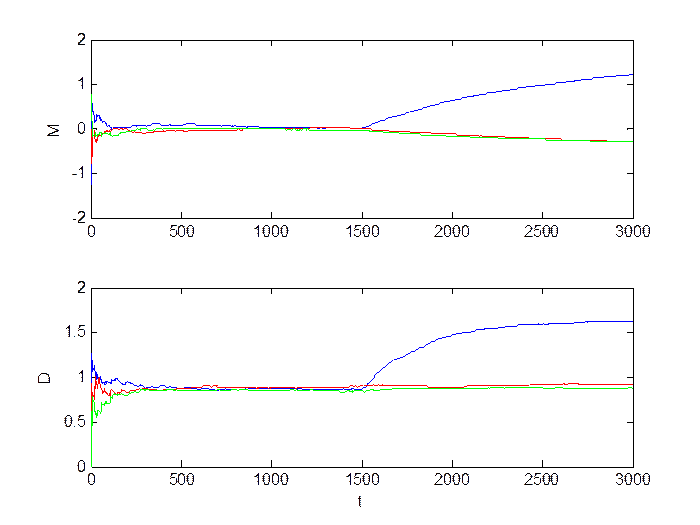
Рис.3.6. Оценка инвариантов.

Малое изменение уровня шумов (M = 0, D = 1.5):

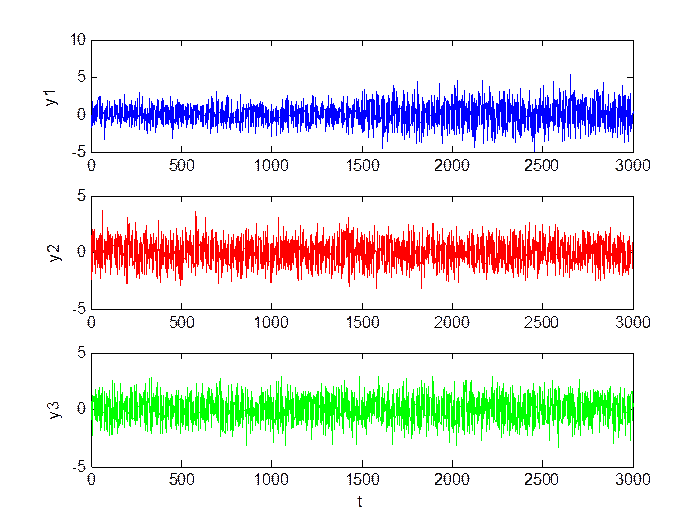
Рис.3.7. Сигнал в каналах.

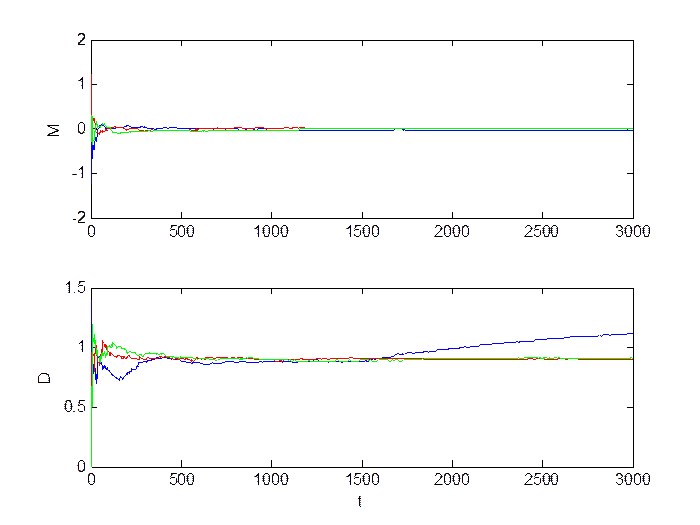
Рис.3.8. Оценка инвариантов.

Среднее изменение уровня шумов (M = 0, D = 2.5):

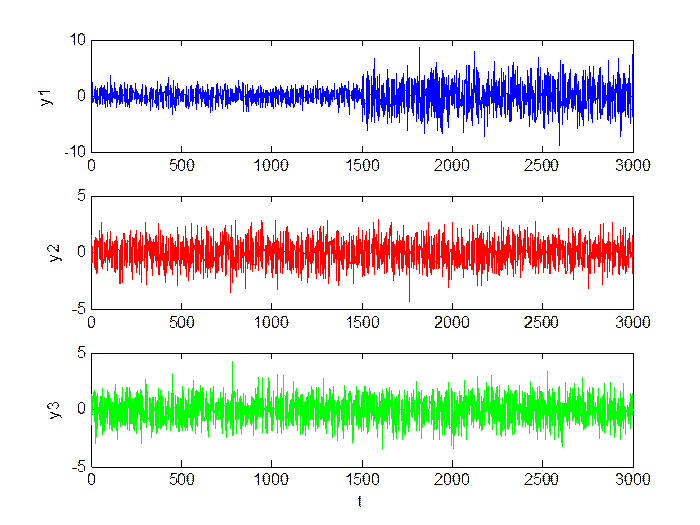
Рис.3.9. Сигнал в каналах.

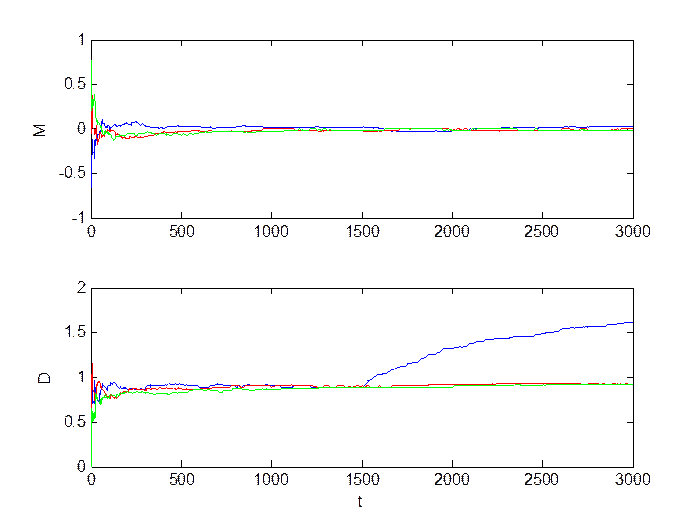
Рис.3.10. Оценка инвариантов.

Большое изменение уровня шумов (M = 0, D = 5):

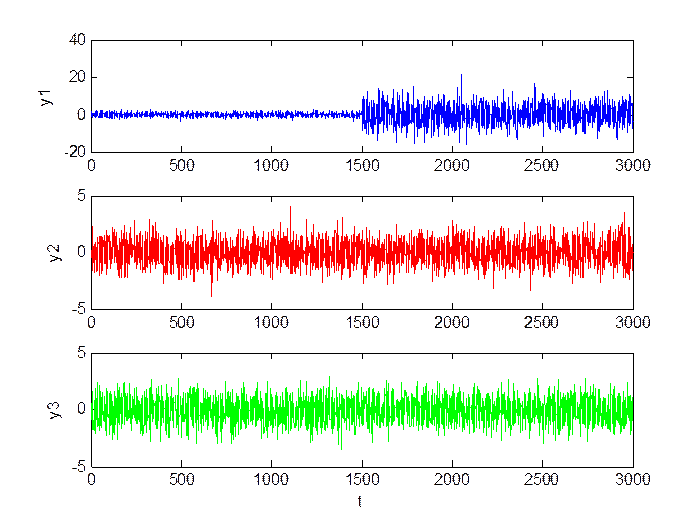
Рис.3.11. Сигнал в каналах.

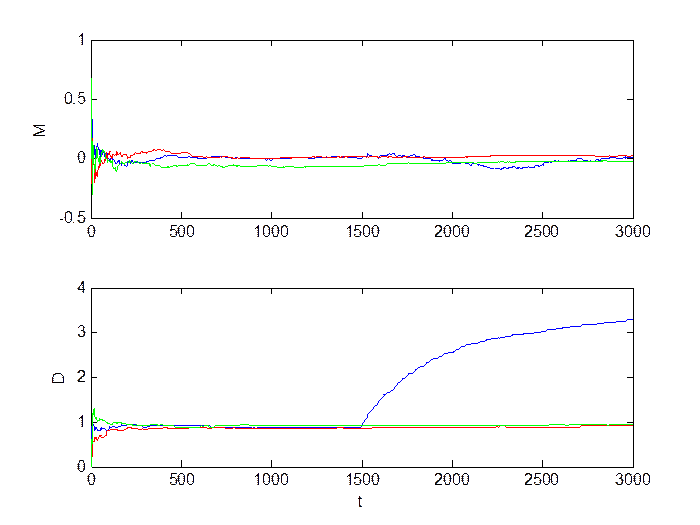
Рис.3.12. Оценка инвариантов.

2. Выводы

В данной работе исследовалась система диагностирования на основе структурных инвариантов различных видов. При моделировании наблюдался вид сигналов в информационных каналах, и производился анализ математического ожидания и дисперсии инвариантов.

При наличии дефекта типа «сдвиг» изменению подвергается как математическое ожидание, так и дисперсия. В случае изменения уровня шума в канале происходит изменение только дисперсии.

В случае использования инвариантов вида «разность одноименных