Информатика и выч. техника \ Идентификация и диагностика систем управления

Моделирование случайных факторов. Графики, иллюстрирующие последовательности случайных чисел и плотности их распределения

Страницы работы

17 страниц (Word-файл)
Скачать файл

Фрагмент текста работы

Санкт-Петербургский государственный политехнический университет

Кафедра компьютерных систем и программных технологий

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1

Дисциплина: Идентификация и диагностика систем управления

Тема: Моделирование случайных факторов

Вариант 10

Выполнил студент гр. 5081/1                                                              

Проверил                                                                                                       

Санкт-Петербург

2010

1. Провести моделирование генерации нормально-распределенных чисел для следующих значений математического ожидания и дисперсии:

математическое ожидание

0

0

1

дисперсия

1

4

4

Выяснить зависимость оценок (точечных и интервальных) математического ожидания и дисперсии от объема выборки () при доверительном уровне .

Графики,  иллюстрирующие  последовательности  случайных  чисел  и  плотности  их распределения НЕ приводить.

Точечные оценки математического ожидания и дисперсии:

·   

· 

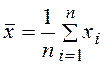
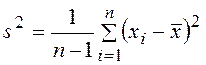
Интервальные оценки математического ожидания и дисперсии для случая неизвестной дисперсии:

·  , где

 –  квантиль распределения Стьюдента с  степенями свободы.

 – доверительная вероятность

* – объем выборки

· 

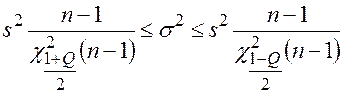
 –  квантиль распределения Хи-квадрат с  степенями свободы.

 – доверительная вероятность

* – объем выборки

Скрипт для проведения моделирования:

clc;

close all;

n=[10,20,50,100,1000];

M=1;

D=4;

q=[0.9, 0.95];

X_=zeros(1,5);

S2=zeros(1,5);

%Для  интервалов с доверительной вероятностью 0.9

X_9=zeros(2,5);

S2_9=zeros(2,5);

%Для  интервалов с доверительной вероятностью 0.95

X_95=zeros(2,5);

S2_95=zeros(2,5);

for i=1:5

x=normrnd(M,D,1,n(i));

X_(i)=mean(x);

S2(i)=std(x)^2

end

for i=1:5

X_9(1,i) = X_(i)-tinv((1+q(1))/2, n(i)-1)*S2(i)/sqrt(n(i));

X_9(2,i) = X_(i)+tinv((1+q(1))/2, n(i)-1)*S2(i)/sqrt(n(i));

X_95(1,i) = X_(i)-tinv((1+q(2))/2, n(i)-1)*S2(i)/sqrt(n(i));

X_95(2,i) = X_(i)+tinv((1+q(2))/2, n(i)-1)*S2(i)/sqrt(n(i));

S2_9(1,i) = S2(i)*(n(i)-1)/chi2inv((1+q(1))/2,n(i)-1);

S2_9(2,i) = S2(i)*(n(i)-1)/chi2inv((1-q(1))/2,n(i)-1);

S2_95(1,i) = S2(i)*(n(i)-1)/chi2inv((1+q(2))/2,n(i)-1);

S2_95(2,i) = S2(i)*(n(i)-1)/chi2inv((1-q(2))/2,n(i)-1);

end

semilogx (n, S2_9(1,:),'g+',n, S2_95(1,:),'r*', n, S2, 'bx');

xlabel('Объем выборки');

ylabel('S^2');

legend('Доверительный уровень=0.9','Доверительный уровень=0.95', 'Точечная оценка');

hold on

semilogx (n, S2_9(2,:),'g+', n, S2_95(2,:),'r*');

grid

figure

semilogx (n, X_9(1,:),'g+',n, X_95(1,:),'r*', n,X_,'bx');

xlabel('Объем выборки');

ylabel('M');

legend('Доверительный уровень=0.9','Доверительный уровень=0.95', 'Точечная оценка');

hold on

semilogx (n, X_9(2,:),'g+', n, X_95(2,:),'r*');

grid

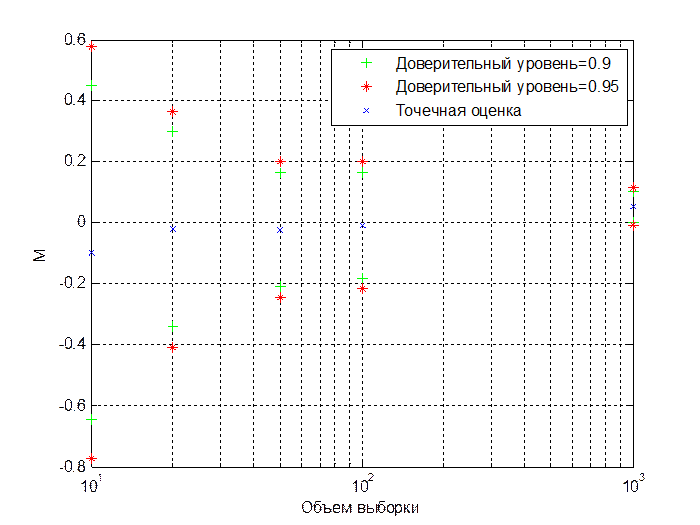
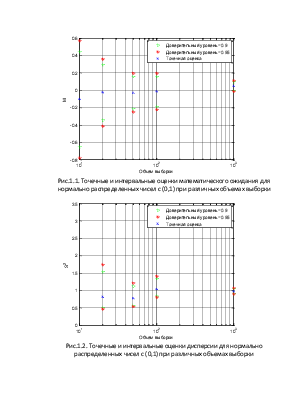
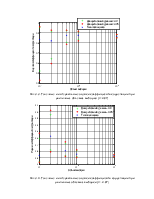
Рис.1.1. Точечные и интервальные оценки математического ожидания для нормально распределенных чисел с (0,1) при различных объемах выборки

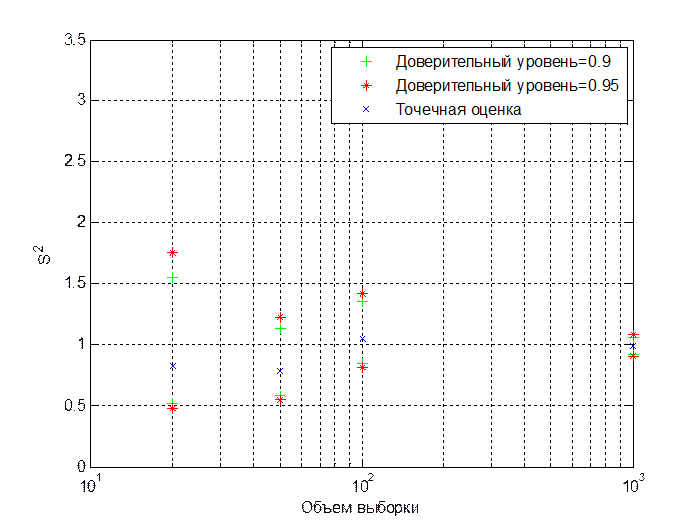
Рис.1.2. Точечные и интервальные оценки дисперсии для нормально распределенных чисел с (0,1) при различных объемах выборки

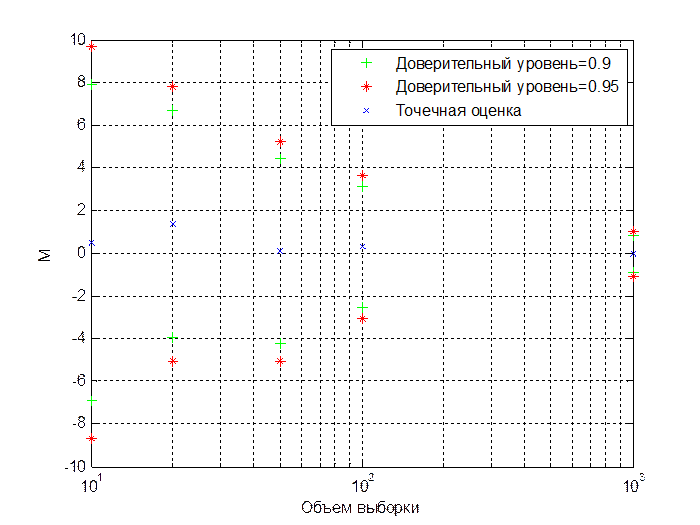
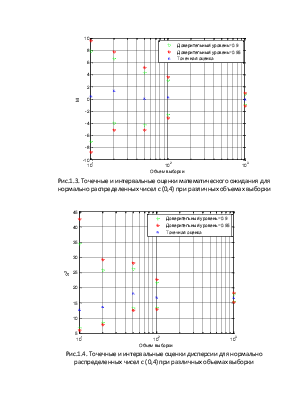
Рис.1.3. Точечные и интервальные оценки математического ожидания для нормально распределенных чисел с (0,4) при различных объемах выборки

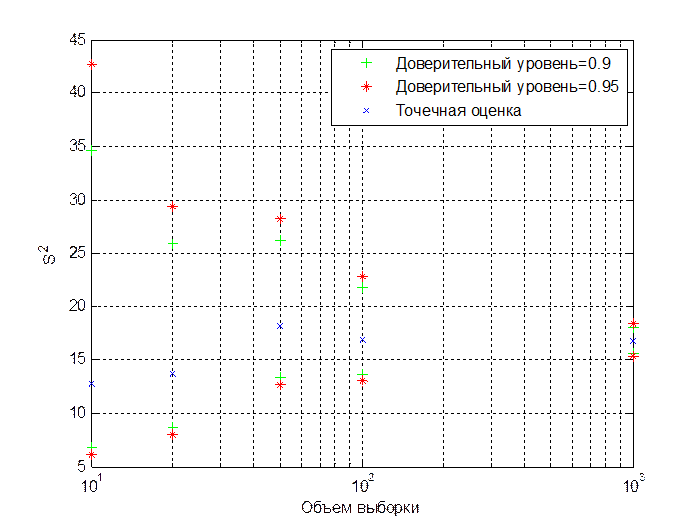
Рис.1.4. Точечные и интервальные оценки дисперсии для нормально распределенных чисел с (0,4) при различных объемах выборки

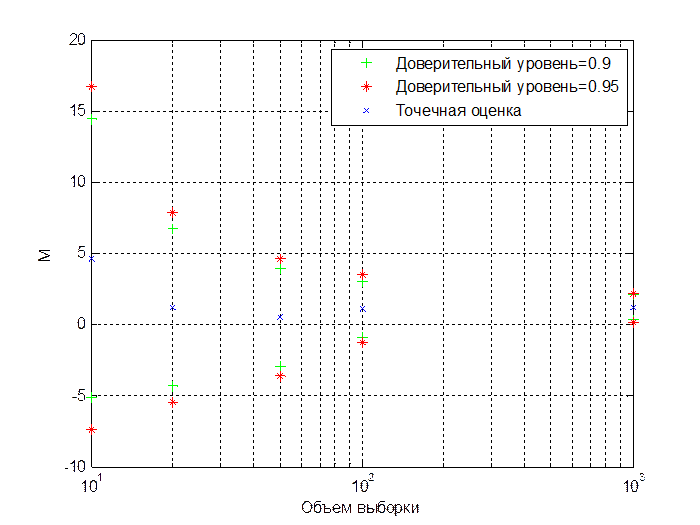
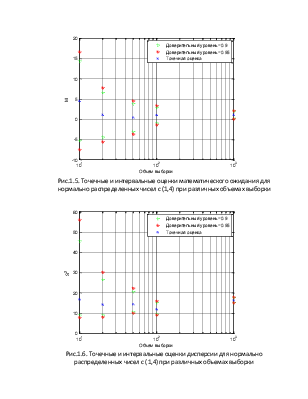
Рис.1.5. Точечные и интервальные оценки математического ожидания для нормально распределенных чисел с (1,4) при различных объемах выборки

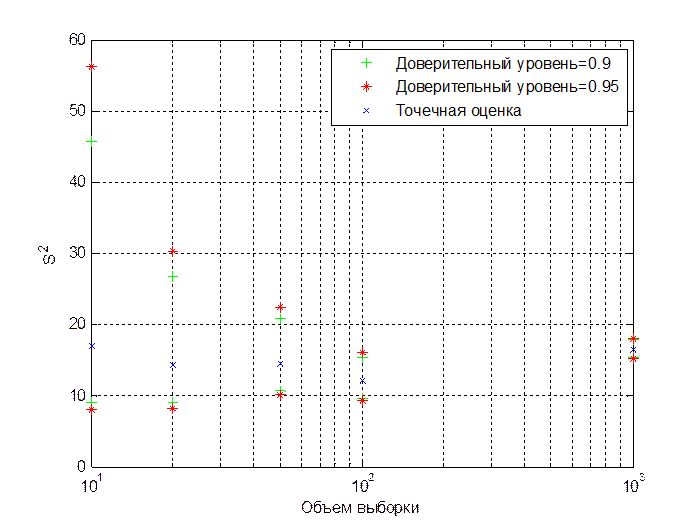
Рис.1.6. Точечные и интервальные оценки дисперсии для нормально распределенных чисел с (1,4) при различных объемах выборки

2. Определить объемы выборки, необходимые для получения доверительного интервала математического ожидания, равного 0,1 при доверительном уровне . Провести моделирование для полученного значения объема выборки.

Объем выборки для оценки математического ожидания:

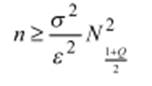
Скрипт для решения уравнения в MATLAB:

clc

q=[0.9, 0.95];

X_9=zeros(2,1);

X_95=zeros(2,1);

M=0;

D=1;

h=0.1;

n_90=(D/(h/2)^2)*(1.282)^2

x=normrnd(M,D,1,n);

Xsr=mean(x);

S2=std(x)^2;

X_9_l = Xsr-tinv((1+q(1))/2, n-1)*S2/sqrt(n);

X_9_h = Xsr+tinv((1+q(1))/2, n-1)*S2/sqrt(n);

interval_90=abs(X_9_l)+abs(X_9_h)

n_95=(D/(h/2)^2)*(1.645)^2

x=normrnd(M,D,1,n);

Xsr=mean(x);

S2=std(x)^2;

X_95_l = Xsr-tinv((1+q(2))/2, n-1)*S2/sqrt(n);

X_95_h =Xsr+tinv((1+q(2))/2, n-1)*S2/sqrt(n);

interval_95=abs(X_95_l)+abs(X_95_h)

Результат:

n_90 =

657.4096

Warning: Size vector should be a row vector with integer elements.

interval_90 =

0.1008

n_95 =

1.0824e+003

Warning: Size vector should be a row vector with integer elements.

interval_95 =

0.1178

3. Провести моделирование генерации вектора нормально-распределенных чисел при размерности 2 и нулевом математическом ожидании для следующих значений корреляционных матриц:

, , , .

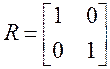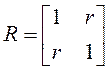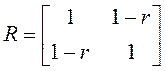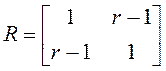Построить оценки заданной корреляционной матрицы и выяснить зависимость оценок от объема выборки.

Построить доверительные интервалы для оценки коэффициента корреляции в зависимости от объема выборки , при доверительном уровне .

Графики,  иллюстрирующие  последовательности  случайных  чисел  и  плотности  их распределения НЕ приводить.

Многомерное нормальное распределение вектора:

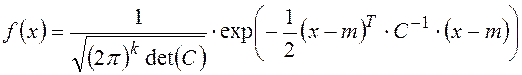
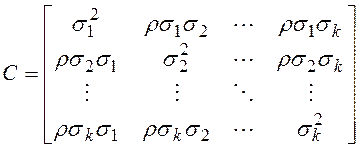
где mi – математическое ожидание хi

С – ковариационная матрица

Это распределение моделируется с помощью линейного преобразования:

X=Ay+mx

Матрица A определяется условием С = ААТ, где А – нижняя треугольная матрица.

y – вектор с распределением N(O,E)

Приближенный доверительный интервал для коэффициента корреляции двумерного нормального распределения, коэффициент корреляции  неизвестен:

 – оценка .

,

,

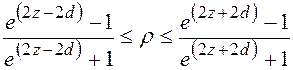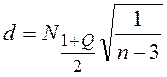
Скрипт для решения в MATLAB:

clc;

close all;

%10й вариант r=0.13

r=0;

%r=0.13;

%r=0.87;

%r=-0.87;

R=[1,r;r,1];

N=[10,20,50,100,1000];

a=[0.9,0.95];

ccof=zeros(1,5);%оценка корреляционной матрицы

R_9=zeros(2,5);%доверительные интервал для a=0.9

R_95=zeros(2,5);%доверительные интервал для a=0.95

A=(chol(R))'

for i=1:5

z1=zeros(N(i),2); z2=z1;

for j=1:N(i)

x1=randn(2,1);  z1(j,:)=x1';

x2=A*x1;  z2(j,:)=x2';

end

r2=cov(z2);

cor_cof=r2(1,2)/sqrt(r2(1,1)*r2(2,2));

ccof(i)=cor_cof;

z=1/2*log((1+cor_cof)/(1-cor_cof));

d=norminv((1+a(1))/2)*sqrt(1/(N(i)-3));

R_9(1,i)=(exp(2*z-2*d)-1)/(exp(2*z-2*d)+1);

R_9(2,i)=(exp(2*z+2*d)-1)/(exp(2*z+2*d)+1);

d=norminv((1+a(2))/2)*sqrt(1/(N(i)-3));

R_95(1,i)=(exp(2*z-2*d)-1)/(exp(2*z-2*d)+1);

R_95(2,i)=(exp(2*z+2*d)-1)/(exp(2*z+2*d)+1);

end

semilogx (N, R_9(1,:),'g+',N, R_95(1,:),'r*', N, ccof, 'bx');

xlabel('Объем выборки');

ylabel('Оценка коэффициента корреляции');

legend('Доверительный уровень=0.9','Доверительный уровень=0.95', 'Точечная оценка');

hold on

semilogx (N, R_9(2,:),'g+',N, R_95(2,:),'r*');

grid

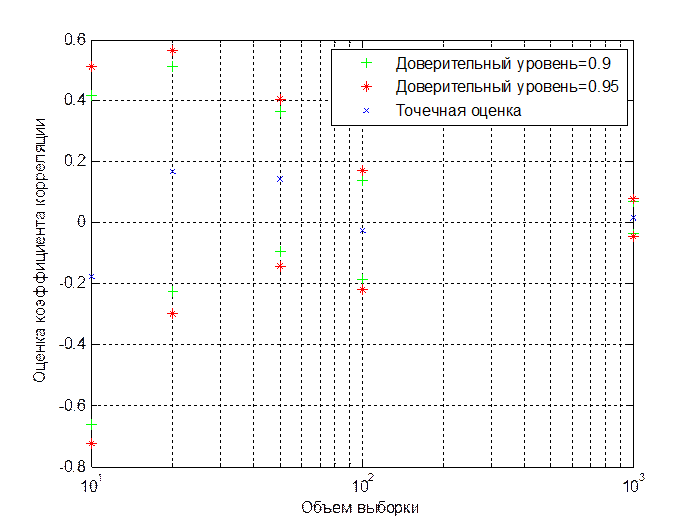
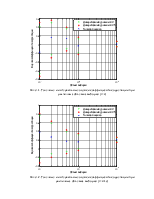
Рис.3.1. Точечные и интервальные оценки коэффициента корреляции при различных объемах выборки (r=0)

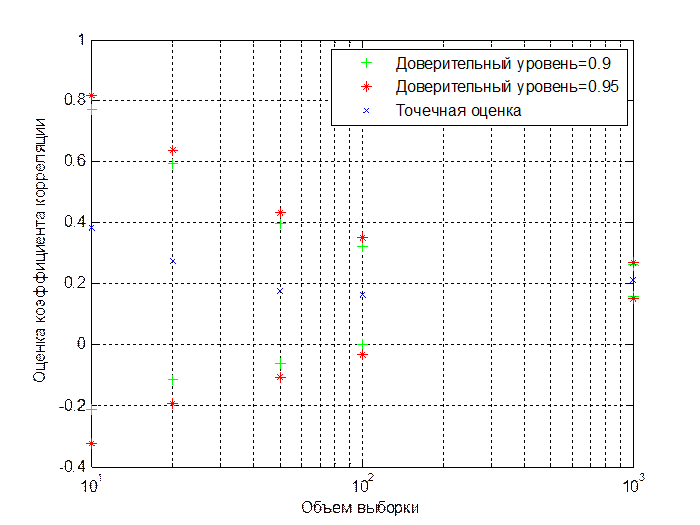
Рис.3.2. Точечные и интервальные оценки коэффициента корреляции при различных объемах выборки (r=0.13)

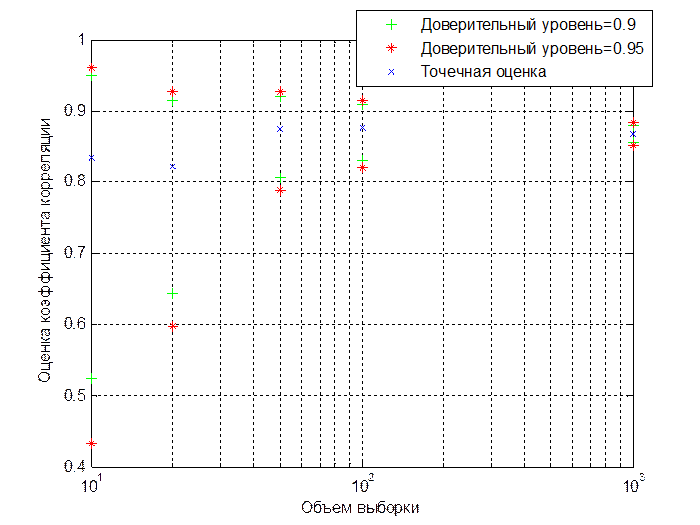
Рис.3.3. Точечные и интервальные оценки коэффициента корреляции при различных объемах выборки (r=0.87)

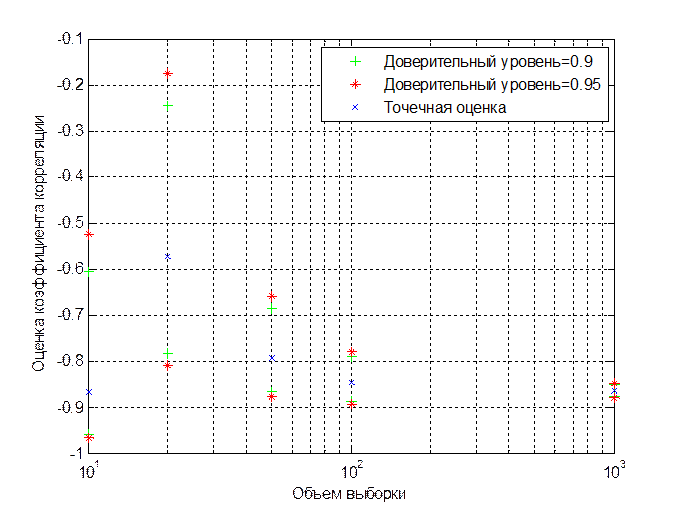
Рис.3.4. Точечные и интервальные оценки коэффициента корреляции при различных объемах выборки (r=-0.87)

4. Провести моделирование генерации случайного процесса, представленного уравнением авторегрессии 1 порядка. Определить оценку коэффициента авторегрессии a1 для 0,3 и 0,75

Уравнение авторегрессии:

,

p – порядок авторегрессии

Уравнение авторегрессии 1-го порядка:

Скрипт для моделирования в Matlab:

clc;

close all;

N=1000;

%a1= 0.3;

a1=0.75;

Mx=0;

Sigma=1;

Beta=Sigma*sqrt(1-a1^2);

X =zeros(1, N);

prevX =0;

for i=1:N   

cX = Mx + a1*(prevX-mx) + Beta*randn;

X(1,i)=cX;

prevX =cX;   

end

r=covf2(X', 5);

ocenka_a1=r(2)

plot(X)

grid

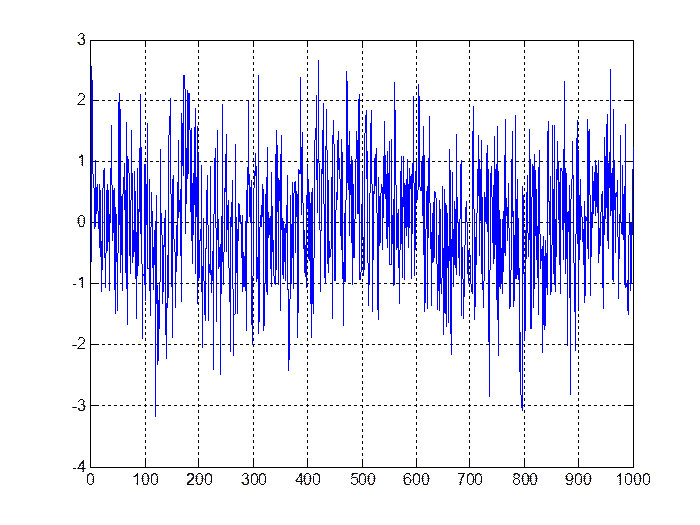
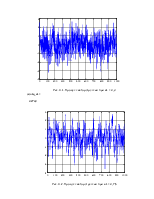
Рис. 4.1. Процесс авторегрессии при а1 = 0,3

ocenka_a1 =

0.2793

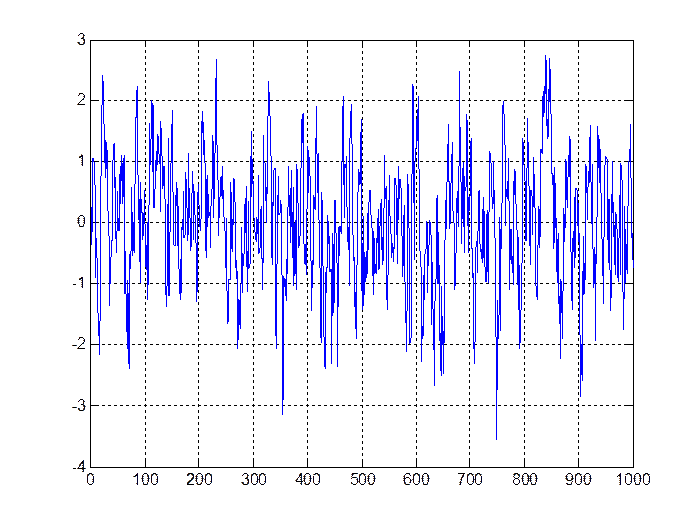
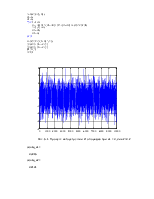
Рис. 4.2. Процесс авторегрессии при а1 = 0,75

ocenka_a1 =

0.7615

5. Для каждого коэффициента авторегрессии  для каждого коэффициента авторегрессии  c целью получения процесса авторегрессии 2 порядка, исходя из условия стационарности случайного процесса

Уравнение авторегрессии второго порядка:

,

,

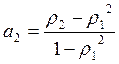
Процесс стационарен, если

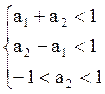
Для а1 = {0,3; 0,75} выберем а2 = {0,2; 0,1}.

6. Провести моделирование генерации случайного процесса, представленного уравнением авторегрессии 2 порядка. Определить оценку коэффициентов авторегрессии  и

Скрипт  Matlab

clc;

close all;

N= 10000;

%a1= 0.3;

%a2=0.2

a1=0.75;

a2=0.1;

Mx=0;

Sigma=1;

Beta=sqrt(Sigma^2*(1+a2)*((1-a2)^2-a1^2)/(1-a2));

X=zeros(1,N);

x0=0;

x1=0;

for i=1:N

x= Mx+a1*(x1-Mx)+a2*(x0-Mx)+Beta*randn;

X(1,i)=x;

x0=x1;

x1=x;

end

r=arcov(X(1:N)',2);

ocenka_a1=-r(2)

ocenka_a2=-r(3)

plot(X)

grid

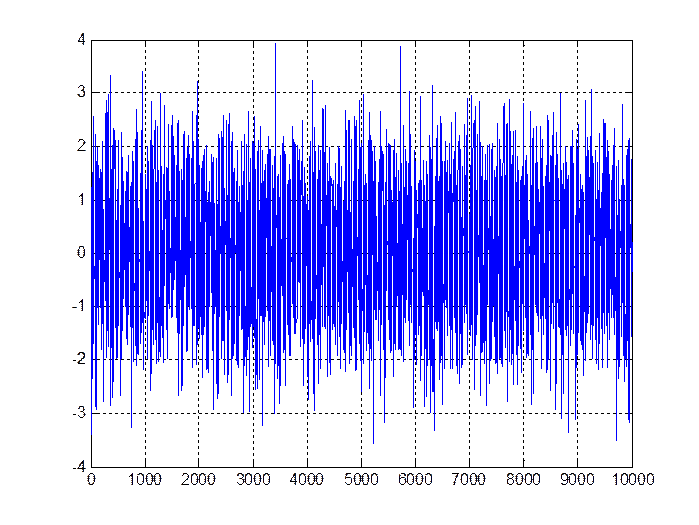
Рис. 6.1. Процесс авторегрессии 2го порядка при а1 = 0,3 и а2=0.2

ocenka_a1 =

0.3016

ocenka_a2 =

0.2101

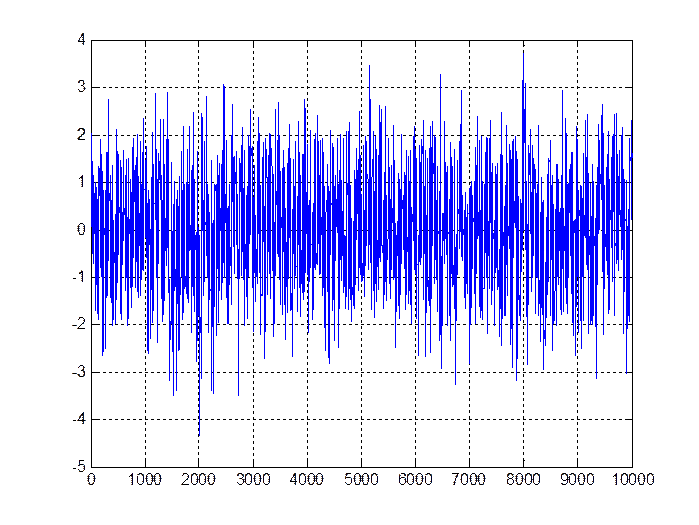
Рис. 6.2. Процесс авторегрессии 2го порядка при а1 = 0,75 и а2=0.1

ocenka_a1 =

0.7267

ocenka_a2 =

0.1332

Выводы

В данной работе проводилось моделирование и исследование  случайных

Похожие материалы

Информация о работе

ВУЗ:
Санкт-Петербургский государственный политехнический университет (СПбГПУ)
Предмет:
Идентификация и диагностика систем управления
Тип:
Отчеты по лабораторным работам
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
255 Kb
Скачали:
0
Скачать файл