Информатика и выч. техника \ Идентификация и диагностика систем управления

Модификация и комплексирование алгоритмов диагностирования. Построенная система диагностирования, для обнаружения изменения параметров объекта диагностирования

Страницы работы

17 страниц (Word-файл)
Скачать файл

Фрагмент текста работы

Корреляционная матрица ошибок фильтрации

X1_ = [sigmx; 0];   % Начальная оценка наблюдения

% Счетчик цикла реализаций (дискретное время)

n = count; 

n1 = count / 2;             % при дефекте

Zi = zeros(1, n);

Zm = zeros(1, n);   % размер матрицы                      

% Цикл реализации работы фильтра

for i = 1:n       

if i == n1

mu1 = mu1+mu1_offset;

sigmy = sigmy * sigmy_offset;

end

% Моделирование состояний

X1 = A*X1 + sigmx*(randn);

Xm(1,i) = X1(1,1);  

% Моделирование наблюдений

Y = C*X1 + sigmy*(randn + Msm);

% Вычисление матричного коэффициента усиления

%  и корреляционной матрицы ошибок экстраполяции

Q = A*P*A' + F*mu1*F';

K = Q*(C')*((C*Q*(C') + sigmy)^-1);

P = Q - K*C*Q;    

% Оценка вектора состояния и вычисление обновляющей

%  последовательности

X1_ = A*X1_ + F*mu1 + K*(Y - C*(A*X1_ + F*mu1));   

Z1 = Y - C*(A*X1_ + F*mu1);

Zi(i) = Z1;

% Нормировочный коэффициент

S = sigmy + C*P*(C') - sigmy*(K')*(C') - C*K*sigmy;

% Нормируем обновляющую последовательность

Z = 0.5*(Z1)*(S^-0.5);

Zm(1,i)=Z;     

% Вычисляем автокорреляционную функцию

r = covf2(Zm',10);

% Оценка коэффициентов

a1_=r(2)*(1-r(3))/(1-r(2)^2);

a2_=(r(3)-r(2)^2)/(1-r(2)^2);

if i == 1 %ASO

S1(i) = alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*(2/pi)^.5+alpha*abs(Zi(i)-mu);

else

S1(i) = (1-alpha)*S1(i-1)+alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*R1(i-1)+alpha*abs(Zi(i)-mu);

end

if  mean (Zi) > mu %AKS

if i == 1

G_AKS(i) = max(0, sign(Zi(i) - mu - vetta/2));

else

G_AKS(i) = max(0, (G_AKS(i-1)+1) * sign(Zi(i)- mu - vetta/2));

end

else

if i == 1

G_AKS(i) = max(0, -sign(Zi(i) - mu + vetta/2));

else

G_AKS(i) = max(0, (G_AKS(i-1)+1) * (-sign(Zi(i)- mu + vetta/2)));

end 

end

if sigmy_offset == 1

G_ASO(i)=S1(i)/R1(i); %ASO

else

G_ASO(i)=R1(i); %ASO

end           

if (((G_ASO(i) >= h2) || (G_ASO(i) <= h1)) && (G_AKS(i) > h))

Def(i) = 1;

else

Def(i) = 0;

end

end

for k = 1:n/2

b(k)=Def(k);

end

Plo(j) = mean(b);

t = 0;

for l = Dfm:n

if Def(l) == 1

t = t + l - Dfm;

break;

end

end

tau(j) = t;

end

%tau_int(1,1) = mean(tau) - tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

%tau_int(1,2) = mean(tau) + tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

%plot(Def, 'black'), hold on;

%plot(G1, 'r'), hold on;

%plot([1,n], [h1,h1], 'black'), hold on;

%plot([1,n], [h2,h2], 'black'), hold on;

%grid;

%xlabel('N');

%ylabel('G');

disp('Вероятность ложного обнаружения:');

disp( mean(Plo) );

disp('Время обнаружения:');

disp( mean(tau) );

%disp('Интервальная оценка времени обнаружения:');

%disp( tau_int );

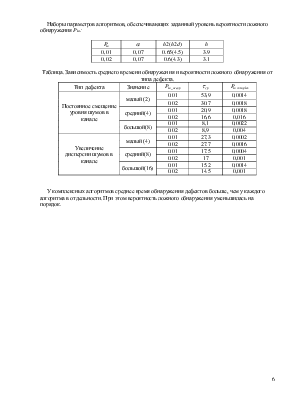
Наборы параметров алгоритмов, обеспечивающих заданный уровень вероятности ложного обнаружения Plo:

0,01

0,07

0.65(4.5)

3.9

0,02

0,07

0.6(4.3)

3.1

Таблица. Зависимость среднего времени обнаружения и вероятности ложного обнаружения от типа дефекта.

Тип дефекта

Значение

Постоянное смещение уровня шумов в канале

малый (2)

0.01

53,9

0,0014

0.02

30.7

0,0018

средний(4)

0.01

20,9

0,0018

0.02

16,6

0,016

большой(8)

0.01

8,1

0,0022

0.02

8,9

0,004

Увеличение дисперсии шумов в канале

малый (4)

0.01

27,3

0,0002

0.02

27.7

0,0016

средний(8)

0.01

17.5

0,0004

0.02

17

0,001

большой(16)

0.01

15.2

0,0014

0.02

14.5

0,001

У комплексных алгоритмов среднее время обнаружения дефектов больше, чем у каждого алгоритма в отдельности. При этом вероятность ложного обнаружения уменьшилась на порядок.

2.  Моделирование модифицированного АКС-м2

Скрипт реализующий модифицированный АКС-м2  ( с глубиной решающей функции )  и оценку вероятности ложного обнаружения.

Моделирование 100 экспериментов по 1000 шагов в каждом.

lab82.m

clear all;

%Plo = zeros(1, 100);

%tau = zeros(1, 100);

figure

% Процесс авторегресии первого порядка x(n) = a1*x(n-1)+g

% Процесс авторегресии второго порядка x(n) = a1*x(n-1)+a2*x(n-2)+g

a1 = 0.2;          % Коэффициент авторегресси a1

a2 = 0.4; % 0 0.4     % Коэффициент авторегресси a2

A = [a1 a2; 1 0];   % Матрица состояния

q = 0.95;       % доверительная вероятность

sigm = 1;   % Дисперсия в канале возмущения

% Вычисляем дисперсию шума возмущения   

sigmx = sigm * sqrt( (1+a2)*((1-a2)^2-a1^2)/(1-a2) );

Nexp = 100;

for j = 1:Nexp    % кол-во экспериментов

count = 1000;    % кол-во шагов

vetta = 4;    % порог чувствительности

%mu1 = 0;        % МО до дефекта

%mu2 = 1;        % МО после дефекта

betta1 = 1;     % дисперсия случайного процесса

G1 = zeros(1, count);

G2 = zeros(1, count);

G3 = zeros(1, count);

S1 = zeros(1, count);

S1m = zeros(1, count);

S2 = zeros(1, count);  

S2m = zeros(1, count);

S3 = zeros(1, count);  

S3m = zeros(1, count);

h = 3.1; %3.9 - 0.01 3.1 - 0.02

deep = 0;

Def = zeros(1,count);

Def(1) = 0;

Dfm = count/2;     % момент возникновения дефекта

mu1 = 0;             % МО шума возмущения

mu = mu1;

mu1_offset = 4; %0 1 2 4 cмещение шума возмущения

Msm = 0;            % Постоянное смещение уровня шумов в канале измерения       

F = [1;0];          % Вектор входа по возмущению

% Параметры наблюдателя

C = [1 0];          % Вектор измерения по состоянию

sigmy = 4;          % Дисперсия шума измерения

sigmy_offset = 1; % 1 1.5 2.5 5% Изменение дисперсии шума измерения

% Начальные условия

X1 = [0; 0];        % Начальное наблюдение

P = [1 0; 0 1];     % Корреляционная матрица ошибок фильтрации

X1_ = [sigmx; 0];   % Начальная оценка наблюдения

% Счетчик цикла реализаций (дискретное время)

n = count; 

n1 = count / 2;             % при дефекте

%Zi = zeros(1, n);

%Zm = zeros(1, n);   % размер матрицы                      

% Цикл реализации работы фильтра

for i = 1:n      

if i == n1

mu1 = mu1+mu1_offset;

sigmy = sigmy * sigmy_offset;

end

% Моделирование состояний

X1 = A*X1 + sigmx*(randn);

Xm(1,i) = X1(1,1);  

% Моделирование наблюдений

Y = C*X1 + sigmy*(randn + Msm);

% Вычисление матричного коэффициента усиления

%  и корреляционной матрицы ошибок экстраполяции

Q = A*P*A' + F*mu1*F';

K = Q*(C')*((C*Q*(C') + sigmy)^-1);

P = Q - K*C*Q;    

% Оценка вектора состояния и вычисление обновляющей

%  последовательности

X1_ = A*X1_ + F*mu1 + K*(Y - C*(A*X1_ + F*mu1));   

Z1 = Y - C*(A*X1_ + F*mu1);

Zi(i) = Z1;

% Нормировочный коэффициент

S = sigmy + C*P*(C') - sigmy*(K')*(C') - C*K*sigmy;

% Нормируем обновляющую последовательность

Z = 0.5*(Z1)*(S^-0.5);

Zm(1,i)=Z;     

% Вычисляем автокорреляционную функцию

r = covf2(Zm',10);

% Оценка коэффициентов

a1_=r(2)*(1-r(3))/(1-r(2)^2);

a2_=(r(3)-r(2)^2)/(1-r(2)^2);

if  mean (Zi) > mu

if i == 1

G1(i) = max(0, sign(Zi(i) - mu - vetta/2));

else

G1(i) = max(0, (G1(i-1)+1) * sign(Zi(i)- mu - vetta/2));

end

else

if i == 1

G1(i) = max(0, -sign(Zi(i) - mu + vetta/2));

else

G1(i) = max(0, (G1(i-1)+1) * (-sign(Zi(i)- mu + vetta/2)));

end 

end

%if(G1(i) < h)

%    Def(i) = 0;

%else

%    Def(i) = 1;

%end

if i > deep

for aaa = 0:deep

if (G1(i-aaa) < h)

Def(i) = 0;

break;

else

Def(i) = 1;

end

end

end

end

for k = 1:n/2

b(k)=Def(k);

end

Plo(j) = mean(b);

t = 0;

for l = Dfm:n

if Def(l) == 1

t = l - Dfm;

break;

end

end

tau(j) = t;

end

tau_int(1,1) = mean(tau) - tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

tau_int(1,2) = mean(tau) + tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

plot(Def, 'black'), hold on;

plot(G1, 'r'), hold on;

plot([1,n], [h,h], 'black'), hold on;

grid;

xlabel('N');

ylabel('G');

disp('Вероятность ложного обнаружения:');

disp( mean(Plo) );

disp('Время обнаружения:');

disp( mean(tau) );

disp('Интервальная оценка времени обнаружения:');

disp( tau_int );

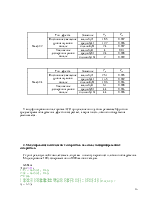
С глубиной, равной нулю, мы делали опыты в предыдущей работе. Возьмем ещё глубину deep= 2 и 4.

Тип дефекта

Значение

Постоянное смещение уровня шумов в канале

малый (2)

39.9

0.002

средний(4)

12.6

0.0008

Deep = 2

большой(8)

6.7

0.0004

Увеличение дисперсии шумов в канале

малый (4)

110

0.0008

средний(8)

92.8

0.0006

большой(16)

84.8

0.0003

Тип дефекта

Значение

Постоянное смещение уровня шумов в канале

малый (2)

142

0

средний(4)

17.3

0.0002

Deep = 4

большой(8)

8

0.0002

Увеличение дисперсии шумов в канале

малый (4)

68.4

0.0004

средний(8)

61.6

0

большой(16)

60

0.0006

С увеличением глубины, вероятность ложного обнаружения уменьшается и увеличивается среднее время обнаружения. Вобщем это и так понятно из теории. А для выявления дефектов дисперсии этот алгоритм плохо подходит.

3.  Моделирование модифицированного алгоритма АСО

Скрипт реализующий модифицированный алгоритм АСО (с глубиной решающей функции)  и оценку вероятности ложного обнаружения.

Моделирование 100 экспериментов по 1000 шагов в каждом.

lab83.m

clear all;

%Plo = zeros(1, 100);

%tau = zeros(1, 100);

figure

% Процесс авторегресии первого порядка x(n) = a1*x(n-1)+g

% Процесс авторегресии второго порядка x(n) = a1*x(n-1)+a2*x(n-2)+g

q = 0.95;

a1 = 0.2;          % Коэффициент авторегресси a1

a2 = 0.4; % 0 0.4     % Коэффициент авторегресси a2

A = [a1 a2; 1 0];   % Матрица состояния

sigm = 1;   % Дисперсия в канале возмущения

% Вычисляем дисперсию шума возмущения   

sigmx = sigm * sqrt( (1+a2)*((1-a2)^2-a1^2)/(1-a2) );

Nexp = 100;

for j = 1:Nexp    % кол-во экспериментов

count = 1000;    % кол-во шагов

vetta = 4;    % порог чувствительности

%mu1 = 0;        % МО до дефекта

%mu2 = 1;        % МО после дефекта

betta1 = 1;     % дисперсия случайного процесса

G1 = zeros(1, count);

G2 = zeros(1, count);

G3 = zeros(1, count);

S1 = zeros(1, count);

R1 = zeros(1, count);

S2 = zeros(1, count);  

S2m = zeros(1, count);

S3 = zeros(1, count);  

S3m = zeros(1, count);

alpha = 0.07;

h1 = -0.6; %0.65 - 0.01 0.6 - 0.02

h2 = 0.6; %4.5 - 0.01; 4.3 - 0.02

deep = 2

Def = zeros(1,count);

Def(1) = 0;

Dfm = count/2;     % момент возникновения дефекта

mu1 = 0;             % МО шума возмущения

mu = mu1;

mu1_offset = 2; %0 1 2 4 cмещение шума возмущения

Msm = 0;            % Постоянное смещение уровня шумов в канале измерения       

F = [1;0];          % Вектор входа по возмущению

% Параметры наблюдателя

C = [1 0];          % Вектор измерения по состоянию

sigmy = 4;          % Дисперсия шума измерения

sigmy_offset = 1; % 1 1.5 2.5 5% Изменение дисперсии шума измерения

% Начальные условия

X1 = [0; 0];        % Начальное наблюдение

P = [1 0; 0 1];     % Корреляционная матрица ошибок фильтрации

X1_ = [sigmx; 0];   % Начальная оценка наблюдения

% Счетчик цикла реализаций (дискретное время)

n = count; 

n1 = count / 2;             % при дефекте

Zi = zeros(1, n);

Zm = zeros(1, n);   % размер матрицы                      

% Цикл реализации работы фильтра

for i = 1:n      

if i == n1

mu1 = mu1+mu1_offset;

sigmy = sigmy * sigmy_offset;

end

% Моделирование состояний

X1 = A*X1 + sigmx*(randn);

Xm(1,i) = X1(1,1);  

% Моделирование наблюдений

Y = C*X1 + sigmy*(randn + Msm);

% Вычисление матричного коэффициента усиления

%  и корреляционной матрицы ошибок экстраполяции

Q = A*P*A' + F*mu1*F';

K = Q*(C')*((C*Q*(C') + sigmy)^-1);

P = Q - K*C*Q;     

% Оценка вектора состояния и вычисление обновляющей

%  последовательности

X1_ = A*X1_ + F*mu1 + K*(Y - C*(A*X1_ + F*mu1));   

Z1 = Y - C*(A*X1_ + F*mu1);

Zi(i) = Z1;

% Нормировочный коэффициент

S = sigmy + C*P*(C') - sigmy*(K')*(C') - C*K*sigmy;

% Нормируем обновляющую последовательность

Z = 0.5*(Z1)*(S^-0.5);

Zm(1,i)=Z;     

% Вычисляем автокорреляционную функцию

r = covf2(Zm',10);

% Оценка коэффициентов

a1_=r(2)*(1-r(3))/(1-r(2)^2);

a2_=(r(3)-r(2)^2)/(1-r(2)^2);

if i == 1

S1(i) = alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*(2/pi)^.5+alpha*abs(Zi(i)-mu);

else

S1(i) = (1-alpha)*S1(i-1)+alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*R1(i-1)+alpha*abs(Zi(i)-mu);

end

if sigmy_offset == 1

G1(i)=S1(i)/R1(i); %ASO

else

G1(i)=R1(i); %ASO

end

%if ((G1(i) < h2) && (G1(i) > h1))

%   Def(i) = 0;

% else

%    Def(i) = 1;

%end

if i > deep

for aaa = 0:deep

if ((G1(i-aaa) < h2) && (G1(i-aaa) > h1))

Def(i) = 0;

break;

else

Def(i) = 1;

end

end

end

end

for k = 1:n/2

b(k)=Def(k);

end

Plo(j) = mean(b);

t = 0;

for l = Dfm:n

if Def(l) == 1

t = t + l - Dfm;

break;

end

end

tau(j) = t;

end

tau_int(1,1) = mean(tau) - tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

tau_int(1,2) = mean(tau) + tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

plot(Def, 'black'), hold on;

plot(G1, 'r'), hold on;

plot([1,n], [h1,h1], 'black'), hold on;

plot([1,n], [h2,h2], 'black'), hold on;

grid;

xlabel('N');

ylabel('G');

disp('Вероятность ложного обнаружения:');

disp( mean(Plo) );

disp('Время обнаружения:');

disp( mean(tau) );

disp('Интервальная оценка времени обнаружения:');

disp( tau_int );

Тип дефекта

Значение

Постоянное смещение уровня шумов в канале

малый (2)

18.5

0.007

средний(4)

12.7

0.006

Deep = 2

большой(8)

7.4

0.007

Увеличение дисперсии шумов в канале

малый (4)

4

0.01

средний(8)

2.4

0.008

большой(16)

2

0.009

Тип дефекта

Значение

Постоянное смещение уровня шумов в канале

малый (2)

25.1

0.005

средний(4)

13.5

0.002

Deep = 4

большой(8)

10.6

0.003

Увеличение дисперсии шумов в канале

малый (4)

6.1

0.008

средний(8)

4.4

0.003

большой(16)

4.4

0.006

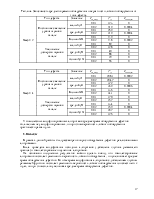
У модифицированного алгоритма АСО при увеличении глубины решающей функции среднее время обнаружения дефектов возрастает, а вероятность ложного обнаружения уменьшается.

4. Моделирование комплексных алгоритмов на основе модифицированных алгоритмов.

Скрипт реализующий комплексные алгоритмы  и оценку вероятности ложного обнаружения.

Моделирование 100 экспериментов по 1000 шагов в каждом.

lab84.m

clear all;

%Plo = zeros(1, 100);

%tau = zeros(1, 100);

%figure

% Процесс авторегресии первого порядка x(n) = a1*x(n-1)+g

% Процесс авторегресии второго порядка x(n) = a1*x(n-1)+a2*x(n-2)+g

q = 0.95;

a1 = 0.2;          % Коэффициент авторегресси a1

a2 = 0.4; % 0 0.4     % Коэффициент авторегресси a2

A = [a1 a2; 1 0];   % Матрица состояния

sigm = 1;   % Дисперсия в канале возмущения

% Вычисляем дисперсию шума возмущения   

sigmx = sigm * sqrt( (1+a2)*((1-a2)^2-a1^2)/(1-a2) );

Nexp = 100;

for j = 1:Nexp    % кол-во экспериментов

count = 1000;    % кол-во шагов

vetta = 4;    % порог чувствительности

%mu1 = 0;        % МО до дефекта

%mu2 = 1;        % МО после дефекта

betta1 = 1;     % дисперсия случайного процесса

G_ASO = zeros(1, count);

G_AKS = zeros(1, count);

G3 = zeros(1, count);

S1 = zeros(1, count);

R1 = zeros(1, count);

S2 = zeros(1, count);  

S2m = zeros(1, count);

S3 = zeros(1, count);  

S3m = zeros(1, count);

alpha = 0.07;

h1 = -0.6; %0.65 - 0.01 0.6 - 0.02

h2 = 0.6; %4.5 -0.01 4.3 - 0.02;

h = 3.1; %AKS 3.9 - 0.01 3.1 - 0.02

deep = 0;

Def = zeros(1,count);

Def(1) = 0;

Dfm = count/2;     % момент возникновения дефекта

mu1 = 0;             % МО шума возмущения

mu = mu1;

mu1_offset = 4; %0 1 2 4 cмещение шума возмущения

Msm = 0;            % Постоянное смещение уровня шумов в канале измерения       

F = [1;0];          % Вектор входа по возмущению

% Параметры наблюдателя

C = [1 0];          % Вектор измерения по состоянию

sigmy = 4;          % Дисперсия шума измерения

sigmy_offset = 1; % 1 1.5 2.5 5% Изменение дисперсии шума измерения

% Начальные условия

X1 = [0; 0];        % Начальное наблюдение

P = [1 0; 0 1];     % Корреляционная матрица ошибок фильтрации

X1_ = [sigmx; 0];   % Начальная оценка наблюдения

% Счетчик цикла реализаций (дискретное время)

n = count; 

n1 = count / 2;             % при дефекте

Zi = zeros(1, n);

Zm = zeros(1, n);   % размер матрицы                      

% Цикл реализации работы фильтра

for i = 1:n       

if i == n1

mu1 = mu1+mu1_offset;

sigmy = sigmy * sigmy_offset;

end

% Моделирование состояний

X1 = A*X1 + sigmx*(randn);

Xm(1,i) = X1(1,1);  

% Моделирование наблюдений

Y = C*X1 + sigmy*(randn + Msm);

% Вычисление матричного коэффициента усиления

%  и корреляционной матрицы ошибок экстраполяции

Q = A*P*A' + F*mu1*F';

K = Q*(C')*((C*Q*(C') + sigmy)^-1);

P = Q - K*C*Q;    

% Оценка вектора состояния и вычисление обновляющей

%  последовательности

X1_ = A*X1_ + F*mu1 + K*(Y - C*(A*X1_ + F*mu1));   

Z1 = Y - C*(A*X1_ + F*mu1);

Zi(i) = Z1;

% Нормировочный коэффициент

S = sigmy + C*P*(C') - sigmy*(K')*(C') - C*K*sigmy;

% Нормируем обновляющую последовательность

Z = 0.5*(Z1)*(S^-0.5);

Zm(1,i)=Z;     

% Вычисляем автокорреляционную функцию

r = covf2(Zm',10);

% Оценка коэффициентов

a1_=r(2)*(1-r(3))/(1-r(2)^2);

a2_=(r(3)-r(2)^2)/(1-r(2)^2);

if i == 1 %ASO

S1(i) = alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*(2/pi)^.5+alpha*abs(Zi(i)-mu);

else

S1(i) = (1-alpha)*S1(i-1)+alpha*(Zi(i)-mu);

R1(i) = (1-alpha)*R1(i-1)+alpha*abs(Zi(i)-mu);

end

if  mean (Zi) > mu %AKS

if i == 1

G_AKS(i) = max(0, sign(Zi(i) - mu - vetta/2));

else

G_AKS(i) = max(0, (G_AKS(i-1)+1) * sign(Zi(i)- mu - vetta/2));

end

else

if i == 1

G_AKS(i) = max(0, -sign(Zi(i) - mu + vetta/2));

else

G_AKS(i) = max(0, (G_AKS(i-1)+1) * (-sign(Zi(i)- mu + vetta/2)));

end 

end

if sigmy_offset == 1

G_ASO(i)=S1(i)/R1(i); %ASO

else

G_ASO(i)=R1(i); %ASO

end

if i > deep

for aaa = 0:deep

if (((G_ASO(i) < h2) && (G_ASO(i) > h1)) || (G_AKS(i) < h))

Def(i) = 0;

break;

else

Def(i) = 1;

end

end

end

%if (((G_ASO(i) >= h2) || (G_ASO(i) <= h1)) && (G_AKS(i) > h))

%    Def(i) = 1;

%else

%    Def(i) = 0;

%end

end

for k = 1:n/2

b(k)=Def(k);

end

Plo(j) = mean(b);

t = 0;

for l = Dfm:n

if Def(l) == 1

t = t + l - Dfm;

break;

end

end

tau(j) = t;

end

%tau_int(1,1) = mean(tau) - tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp);

%tau_int(1,2) = mean(tau) + tinv( (1+q)/2, Nexp-1 ) * std(tau) / sqrt(Nexp

Похожие материалы

Информация о работе

ВУЗ:
Санкт-Петербургский государственный политехнический университет (СПбГПУ)
Предмет:
Идентификация и диагностика систем управления
Тип:
Отчеты по лабораторным работам
Категория:
Информатика и выч. техника (Технические предметы)
Размер файла:
250 Kb
Скачали:
0
Скачать файл