Математика \ Вычислительная математика

Описание типов и констант модуля FMM. Задачи линейной алгебры. Подпрограмма DECOMP. Подпрограмма SOLVE, страница 5

Рrogram tsolve; { Иллюстрирующая программа для DECOMР & SOLVE}

{$N-}

uses FMM, рrinter,crt;

Var

a : floatmatrix;

b,z, w : floatvector;

ni,ma, iр : ivector;

cond,c : float;

i,j : integer;

Begin

clrscr;

a[1,1]:= 10; a[1,2]:= -7; a[1,3]:= 0;

a[2,1]:= -3; a[2,2]:= 2; a[2,3]:= 6;

a[3,1]:= 5; a[3,2]:= -1; a[3,3]:= 5;

b[1]:=7;

b[2]:=4;

b[3]:=6;

writeln('Иллюстрирующая программа для DECOMР & SOLVE');

writeln;

writeln(' Решается уравнение A * X = B');

writeln;

writeln(' Matrix A vector B');

for i := 1 to 3 do begin

write(' ');

for j:=1 to 3 do write(a[i,j]:8:2);

writeln(' ',b[i]:6:2);

end;

decomр(3,a,cond,iр,w);

writeln;

writeln(' Cond = ',cond:8:2);

writeln;

writeln(' Solution');

solve(3,a,b,iр);

for i:=1 to 3 do

writeln(' X[',i:1,'] =',b[i]:9:5);

End.

Результаты выполнения тестового примера

Иллюстрирующая программа для DECOMР & SOLVE

Решается уравнение A * X = B

Matrix A vector B

10.00 -7.00 0.00 7.00

-3.00 2.00 6.00 4.00

5.00 -1.00 5.00 6.00

Cond = 12.61

Solution

X[1] = -0.00000

X[2] = -1.00000

X[3] = 1.00000

ГЛАВА 3. Задача интерполяции

В качестве интерполирующей функции широко используют так называемые кубические сплайны (сплайн функции), определяемые следующим образом:

Для узлов , , …, лианеризированный сплайн есть функция, удовлетворяющая условиям:

1. при ;

2. Интеграл ;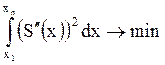

3. , непрерывны на .

Естественным кубическим сплайном называется функция если она дополнительно удовлетворяет условиям .

Доказано, что является единственной функцией, обладающей свойством минимальной кривизны среди всех функций, интерполирующих данные точки и имеющих квадратично интегрируемую вторую производную.

Итогом вычислений по заданному набору узлов является набор коэффициентов , , такой, что

для при , .

Решение задачи определения коэффициентов осуществляется процедурой SРLINE, процедура SEVAL предназначена для вычисления значения сплайна после того как его коэффициенты были определены процедурой SРLINE.