Циклические коды. Выбор образующего многочлена. Расстановка несущих частот модемов. Многопозиционная модуляция. Удельная скорость передачи информации

1. Циклические коды. Выбор образующего многочлена

Корректирующими называют коды, позволяющие обнаруживать и исправлять независимые и зависимые ошибки в принимаемых кодовых последовательностях. Корректирующийкод отличается от простого прежде всего тем, что для кодирования используются не все комбинации, а только часть из них. Эти комбинации называются разрешенными. Остальные комбинации называются запрещенными.

Циклические коды находят наибольшее распространение в системах передачи данных с обратной связью, что обусловлено их высокими корректирующими свойствами, сравнительно простой реализацией, не высокой избыточностью. Особенно они эффективны при обнаружении пакетов ошибок. Циклические коды относятся к блочным систематическим кодам, в которых каждая комбинация кодируется самостоятельно в виде блока таким образом, что информационные r и проверочные r элементы всегда находятся на определенных местах. Кодирование передаваемого сообщения осуществляется умножением двоичной последовательности G(x) на одночлен x^r , имеющий туже степень, что и образующий полином P(x), с добавлением к этому произведению остатка R(x), полученного после деления произведения G(x) x ^r на образующий полином, т.е. передаваемое в канал сообщение F(x) имеет вид:F(x) = G(x) x ^r + R(x).

Выбор кода позволяющего обнаруживать и исправлять ошибки является одной из основных задач при проектировании СПДС и каналообразующих устройств.

Корректирующие свойства любых кодов зависят от их возможности обнаруживать и исправлять ошибки, что в свою очередь зависит от так называемого минимального кодового расстояния всей совокупности кодовых комбинаций кода.

В общем случае код позволяет гарантийно обнаружить любые d-кратные ошибки, если выполняется следующее соотношениеd _min ³ d+1.

Для гарантийного исправления ошибки кратности до s включительно необходимо и достаточно чтобы d _min ³ 2s+1. Из всех известных линейных и систематических кодов наибольшее применение получили циклические коды, которые позволяют обнаруживать и исправлять как независимые ошибки малой кратности, так и группирующие ошибки. Корректирующие свойства циклических кодов зависят от степени и количества отличных от нуля коэффициентов порождающего многочлена g(x)= a _r x ^r + a _r-1 x ^r-1 +…+ a ₁ x + a ₀ , где а _i – двоичный символ кодовой комбинации.

Многочлен циклического кода можно выбрать, используя из условия его неприводимости, т.е. многочлен x ⁿ +1 должен без остатка делится на образующий многочлен степени r.  Кодовые комбинации циклического кода формируются одним из следующих способов:             Умножением каждой k - символьной комбинации исходного кода (k = n - r  ) на порождающий многочлен g(x) степени r (для непрерывного кода). Умножением каждой k - символьной комбинации на x ^r и добавлением к полученному произведению остатка от деления этого произведения на порождающий многочлен (для блочного кода).

Так образующий многочлен по рекомендации V.41 имеет видg(x) = x¹⁶ + x¹² + x⁵ + 1, который часто обозначается как МККТТ-16.

Другим широко используемым 16 разрядным многочленом ( CRC-16 ) является многочлен g(x) = x¹⁶ + x¹⁵ + x² + 1, который приобрел широкую известность как часть протокола двоичной синхронной передачи.

Увеличение числа разрядов и степени полинома многочлена позволяет значительно повысить корректирующую способность кода и верность передачи. Образующий многочлен МККТТ-32 стандартизован МСЭ-Т и известен как CRC-32

g(x) = x³² + x²⁶ + x²³ + x²² + x¹⁶ + x¹² + x¹¹ + x¹⁰ + x⁸ + x⁷ + x⁵ + x⁴ + x² + x +1.

Выбор кода определяется статистикой помех в канале. Коды могут быть разбиты на две группы: блочные, в которых кодирование и декодирование осуществляется в пределах кодовой комбинации, и сверхточные (непрерывные), в которых символы обрабатываются непрерывно, без разделения на блоки. Значительная часть кодов относится к разряду линейных. Их формирование и обработка осуществляются с использованием линейных операций над кодовыми словами. Многие из них обладают свойством цикличности, что значительно упрощает построение схем за счет использования регистров сдвига.

2. Расстановка несущих частот модемов

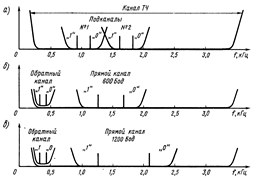
В модемах на 200 бит/с для организации одновременной передачи в обоих направлениях полосу частот канала ТЧ разделяют на два более узких подканала Подканал №1 с частотами ЧМ-сигналов 980 и 1180 Гц предназначен для передачи данных с вызывающей станции, а подканал № 2 с ЧМ-сигналами 1650 и 1850 Гц - для приема данных на вызывающей станции.

В модеме на 600/1200 бит/с полоса частот канала ТЧ делится также на два  подканала. Один канал (прямой передачи) с частотами ЧМ-сигналов 1300 и 1700 Гц или 1300 и 2100 Гц предназначен для передачи данных соответственно со скоростью 600 или 1200 бит/с. Второй канал (обратной связи) с частотами 390 и 450 Гц предназначен для передачи сигналов запроса (подтверждения) со скоростью 75 бит/с.