Скремблирование — это обратимое преобразование структуры цифрового потока без изменения скорости передачи с целью получения свойств случайной последовательности. Скремблирование производится на передающей стороне с помощью скремблера, реализующего логическую операцию суммирования по модулю два исходного и псевдослучайного двоичных сигналов. На приемной стороне осуществляется обратное преобразование — дескремблирование, выполняемое дескремблером. Дескремблер выделяет из принятой последовательности исходную информационную последовательность.
По заданию необходимо построить скремблер с параметрами М = 11 и N = 9. Число M показывает разрядность регистра, а N – ячейка памяти регистра с которой происходит суммирование по модулю два разряда M регистра.
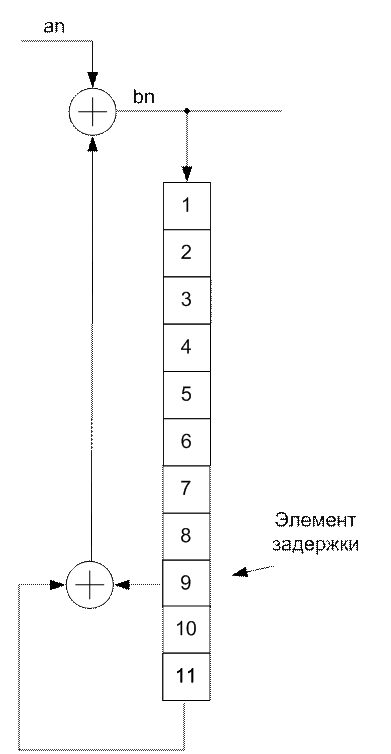
Рисунок 2 – Схема скремблирования
Как видим, устройство скремблера предельно просто. Его реализация возможна как на электронной, так и на электрической базе, что и обеспечило его широкое применение в полевых условиях. Более того, тот факт, что каждый бит выходной последовательности зависит только от одного входного бита, еще более упрочило положение скремблеров в защите потоковой передачи данных. Это связано с неизбежно возникающими в канале передаче помехами, которые могут исказить в этом случае только те биты, на которые они приходятся, а не связанную с ними группу байт, как это имеет место в блочных шифрах.
Декодирование заскремблированных последовательностей происходит по той же самой схеме, что и кодирование. Именно для этого в алгоритмах применяется результирующее кодирование по модулю два – схема, однозначно восстановимая при раскодировании без каких-либо дополнительных вычислительных затрат. Произведем декодирование полученного фрагмента.

Рисунок 3 – Схема дескремблирования
Циклические коды находят наибольшее распространение в системах передачи данных с обратной связью, что обусловлено их высокими корректирующими свойствами, сравнительно простой реализацией, не высокой избыточностью. Особенно они эффективны при обнаружении пакетов ошибок.
Выбор кода позволяющего обнаруживать и исправлять ошибки является одной из основных задач при проектировании каналообразующих устройств.
Корректирующие свойства любых кодов зависят от их возможности обнаруживать и исправлять ошибки, что в свою очередь зависит от так называемого минимального кодового расстояния всей совокупности кодовых комбинаций кода.
По заданию необходимо построить кодер
циклического кода по полиному: ![]() . Схема кодирования представлена на рисунке 4.
. Схема кодирования представлена на рисунке 4.

Рисунок 4 – Схема кодирования циклическим кодом
Таблица 1 – Состояние регистров при кодировании
|
Такт |
Вход |
R0 |
R2 |
Р6 |
Р16 |
S1 |
S2 |
S3 |
Выход |
|
1 |
1 |
1 |
0 |
0 |
0 |
1+0 |
1+1 |
0+1 |
1 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
3 |
1 |
1 |
1 |
0 |
0 |
1+1 |
0+0 |
1+0 |
1 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
5 |
0 |
0 |
1 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
7 |
1 |
1 |
0 |
1 |
0 |
1+1 |
0+0 |
1+0 |
1 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
9 |
0 |
0 |
1 |
1 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
11 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
12 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
13 |
0 |
0 |
0 |
1 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
14 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
15 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
16 |
0 |
0 |
0 |
0 |
0 |
0+1 |
1+1 |
0+1 |
1 |
|
17 |
1 |
1 |
0 |
0 |
1 |
1+1 |
0+0 |
1+0 |
1 |
На выходе кодера кодовая комбинация начинает появляться, начиная с такта 18.
Заключение
В данной контрольной работе был произведен расчет параметров каналообразующего устройства, расчет спектра модулированного сигнала и построена коммутируемая схема каналообразующего устройства, работающая
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.