Исследование детерминированных процессов. Синтезирование процессов во временной области

Лабораторная работа № 1

Исследование детерминированных процессов

Вариант 4

Выполнил

5 курс 1 группа

Цель работы: изучить гармонические, периодические, квазипериодические и непериодические процессы. При исследовании необходимо решить следующее задачи:

- синтезировать процессы во временной области;

- вычислить корреляционные характеристики;

- вычислить спектральные характеристики.

Частота основного тона гармонических и периодических процессов должна быть кратна и не кратна разрешению по частоте (длительность реализации кратна и не кратна периоду основного тона). В качестве периодических рассмотреть «меандр», «равнобокую» и «кособокую» пилу –    |_|ˉˉ|_|ˉˉ|_|ˉˉ|_|ˉˉ|_     /|/|/|/|/|/|     |\|\|\|\|\|\     /\/\/\/\/\/\/.

Важные параметры в моделировании процессов следующие:

f_s = 75 Гц;                         частота сигнала

F_d =880 Гц;                       частота дискретизации  

N=88;                               число отсчетов сигнала

Δt = 1/F_d =0,001136 с;     интервал дискретизации

T = N * Δt =0,1 с;            длительность реализации  

Δf = F_d / N =10 Гц;          разрешение по частоте;

F_d /2 =440 Гц;                  полоса анализа сигнала.

1.  Синтезированные процессы (F_d=880, f_s=75). Для наглядности приведены только первые 0.04 с процесса.

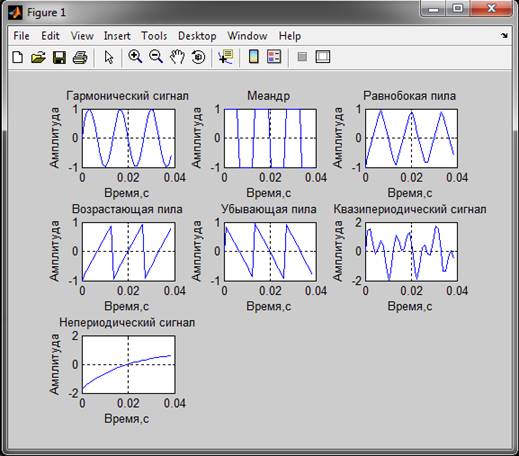
Мощность сигналов:

кратный T                не кратный T

Гармонический сигнал                    0.49998                       0.50227

Меандр                    1.01133                       1.00454

Равнобокая пила                    0.34478                       0.33569

Возрастающая пила                    0.33902                       0.33289

Убывающая пила                    0.32766                       0.32380

Квазипериодический сигнал                  0.99254                      1.00103

Непериодический сигнал                     0.67933                      1.00103

Вывод: полученные оценки мощности для различных длительностей реализаций практически совпадают.

2. Корреляционные характеристики

   

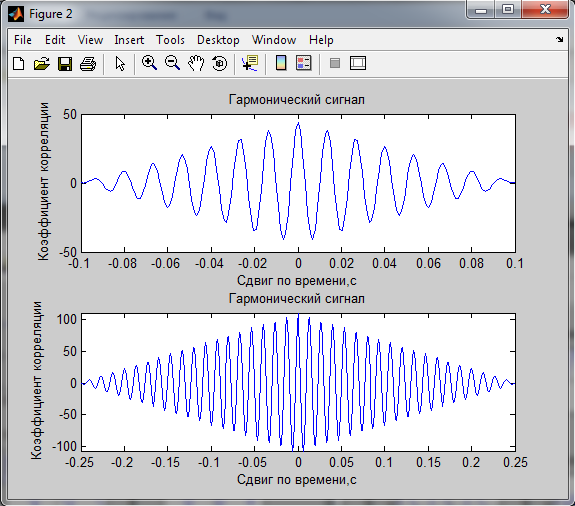
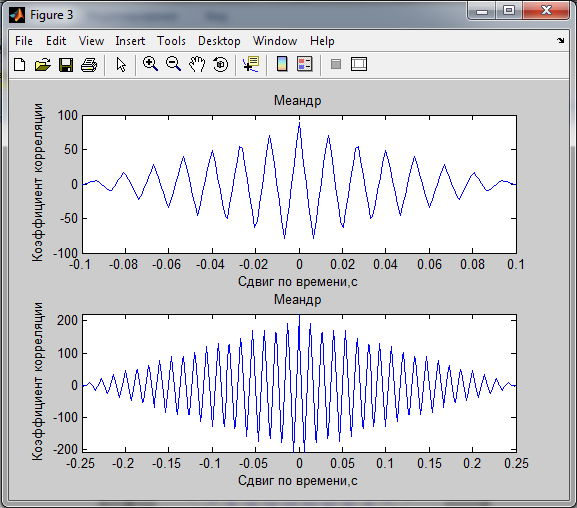
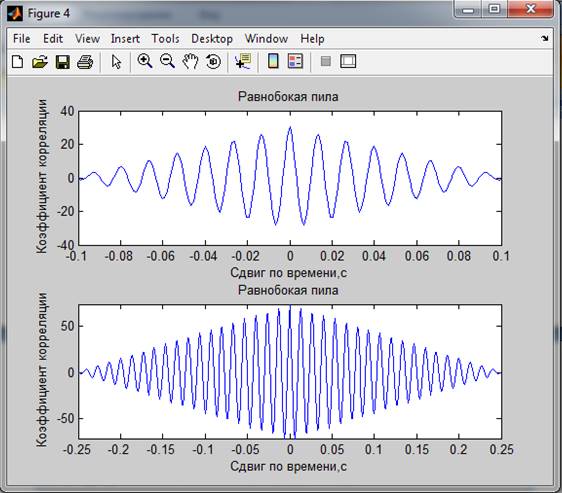
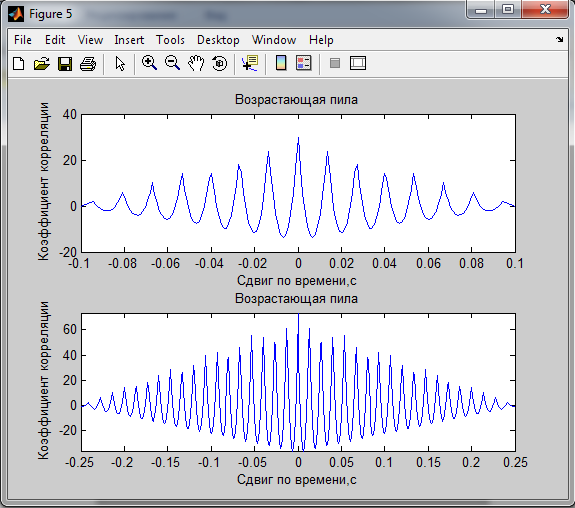
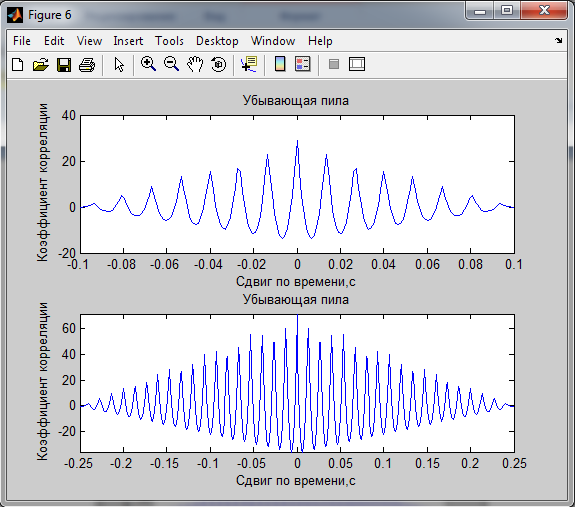
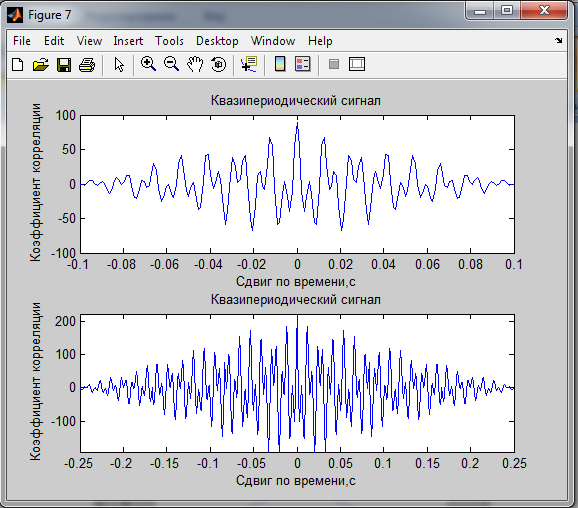
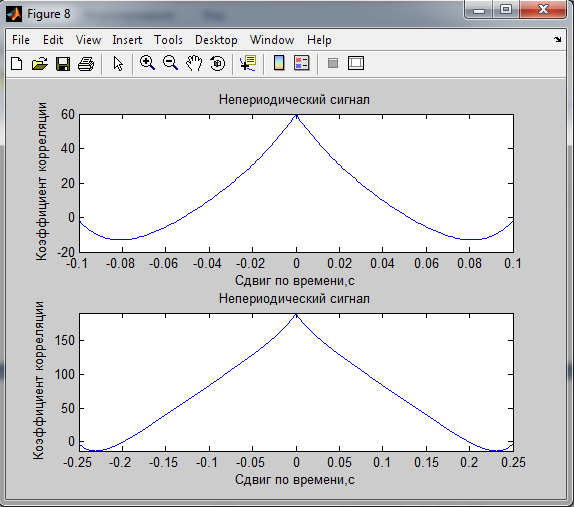
Мощность сигналов по корреляционной функции:

кратный T сигнала                не кратный T

Гармонический сигнал                0.50000                              0.50227

Меандр                1.01136                               1.00455

Равнобокая пила                0.34478                               0.33569

Возрастающая пила                0.33904                               0.33289

Убывающая пила               0.32767                                0.32380

Квазипериодический сигнал              1.01748                               1.01276

Непериодический сигнал                 0.68164                               0.86982

Вывод: Оценки мощности по автокорреляционной функции почти совпадают с оценками, полученными ранее.

4. Спектральные характеристики.

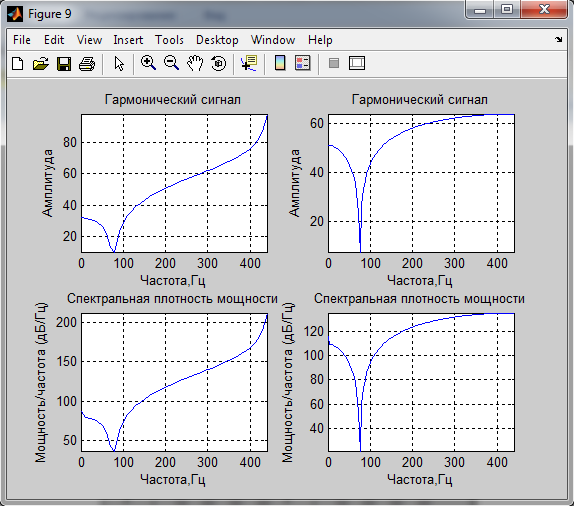
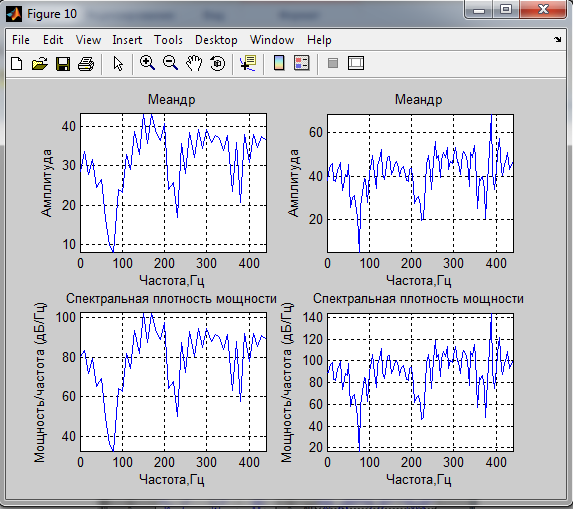
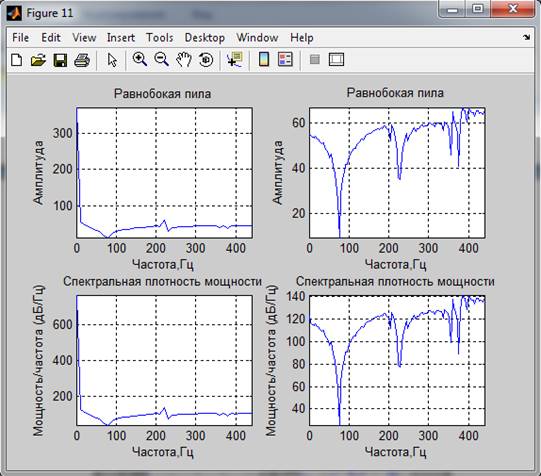
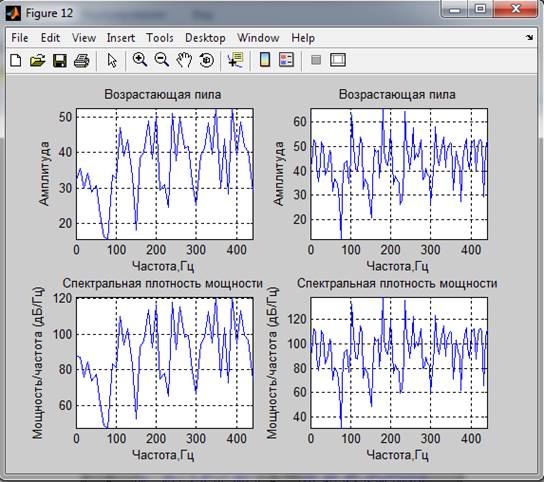
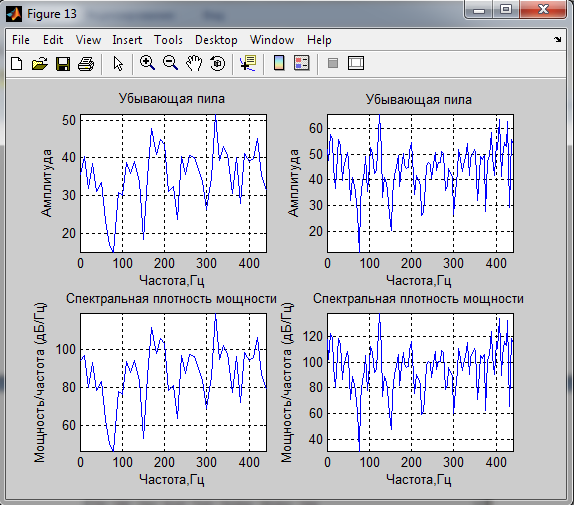
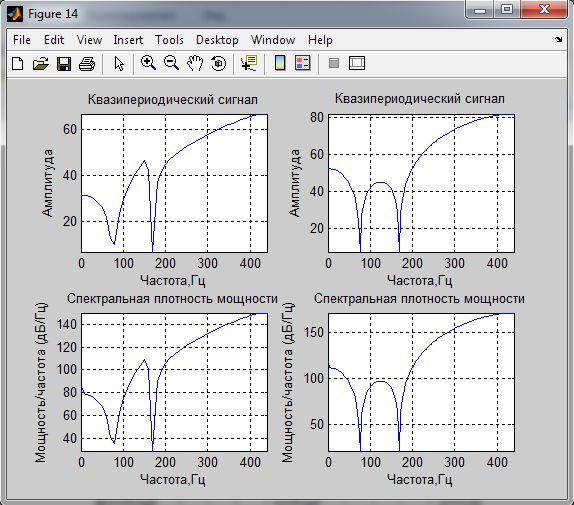
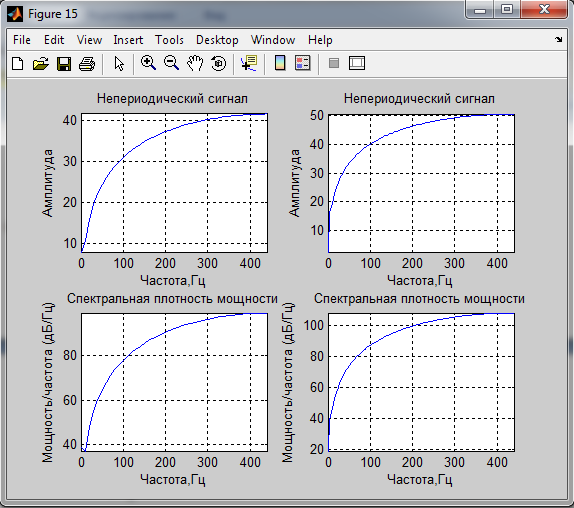
мощность сигналов по спектральным характеристикам:

кр.периоду                 некр.периоду

Гармонический сигнал                 0.50568                      0.50456

Меандр                1.02286                      1.00911

Равнобокая пила                 0.34870                      0.33722

Возрастающая пила                0.34289                       0.33440

Убывающая пила                 0.33140                       0.32527

Квазипериодический сигнал              1.02905                       1.01736

Непериодический сигнал                 0.68939                       0.87378

Вывод: Спектр сигналов, длительность реализации которого была кратна периоду основного тона, имеет более выраженные пики. Так же оценки мощности сигнала, полученные с помощью спектральной плотности мощности соответствуют полученным ранее оценкам.

Код программы:

clc;

clear;

F=75;                                      %частота сигнала

Fd=880;                                    %частота дискретизации

Fdop=F*sqrt(5);                            %доп.частота

Tkr=0.1;                                   %время выборки кратное периоду

Nkr=Fd*Tkr;                                %число отсчетов

Tnekr=0.25;                                %время выборки не кратное периоду

Nnekr=Fd*Tnekr;                            %число отсчетов

t_kr=0:1/Fd:Tkr;                           %вектор времени (кратный Т)

t_nekr=0:1/Fd:Tnekr;                       %вектор времени (не кратный Т)

%Создание сигналов

fprintf('Мощность сигналов:\n');

fprintf('Интервал наблюдения кратный T сигнала|не кратный T\n');

%Гармонический сигнал

krSig(1,:)=sin(2*pi*F*t_kr);

nekrSig(1,:)=sin(2*pi*F*t_nekr);

names{1}='Гармонический сигнал';

%Математическое ожидание сигнала

krMean=mean(sin(2*pi*F*t_kr));           

nekrMean=mean(sin(2*pi*F*t_nekr));  

%Дисперсия сигнала

krCov=cov(sin(2*pi*F*t_kr));              

nekrCov=cov(sin(2*pi*F*t_nekr));  

%Мощность сигнала

krPower=krMean.^2+krCov;                  

nekrPower=nekrMean.^2+nekrCov;     

fprintf('%25s%11.5f%11.5f\n',names{1},krPower,nekrPower);

%Меандр

krSig(2,:)=square(2*pi*F*t_kr);            

nekrSig(2,:)=square(2*pi*F*t_nekr);       

names{2}='Меандр';

%Математическое ожидание сигнала

krMean=mean(square(2*pi*F*t_kr));         

nekrMean=mean(square(2*pi*F*t_nekr));   

%Дисперсия сигнала

krCov=cov(square(2*pi*F*t_kr));           

nekrCov=cov(square(2*pi*F*t_nekr));    

%Мощность сигнала

krPower=krMean.^2+krCov;