Белорусский Государственный Университет
Факультет Радиофизики и Компьютерных технологий
Лабораторная работа № 4
Измерение спектральных характеристик стохастических процессов в реальном масштабе времени
Вариант 5
Выполнил
5 курс 5 группа
Минск 2013
Цель работы:
1. Провести исследование аддитивной модели смеси сигнала и «белого» гауссовского шума с различным отношением сигнал/шум. Выделить сигнал из шума для различных значений разрешающей способности анализа.
2. Подтвердить результаты моделирования реальным экспериментом с анализатором СК4-72.
.
Важные параметры в моделировании процессов следующие:
fs = 2250 Гц; частота сигнала(случай кратной t сигнала)
fs = 2249 Гц; частота сигнала(случай некратной t сигнала)
Fd = 22500 Гц; частота дискретизации
N = 10000-1 , 1000-1; число отсчетов сигнала
Δt = 1/Fd =4.4 * 10^-5 с; интервал дискретизации
T = N * Δt =0.0044 с; длительность реализации
Δf = Fd / N =227 Гц; разрешение по частоте;
Fd /2 =11250 Гц; полоса анализа сигнала.
10000-1 отсчетов (1 случай)
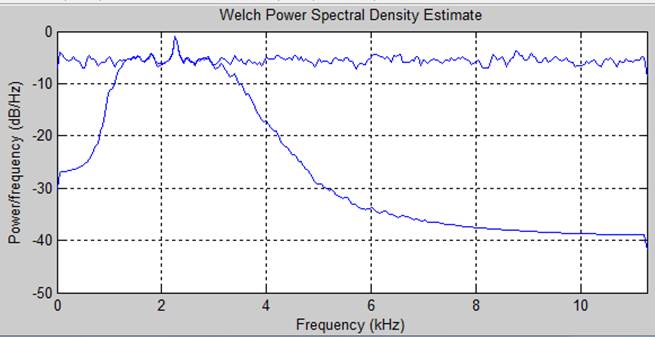
Спектральная плотность мощности исходного сигнала и отфильтрованного
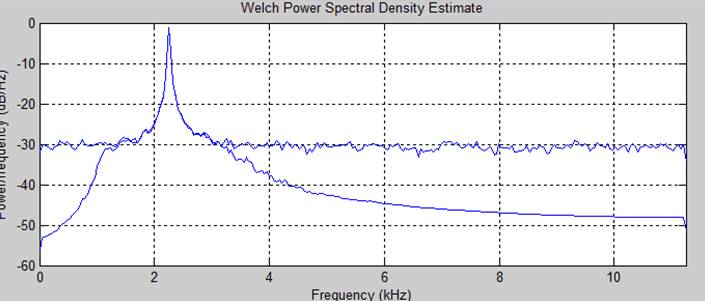
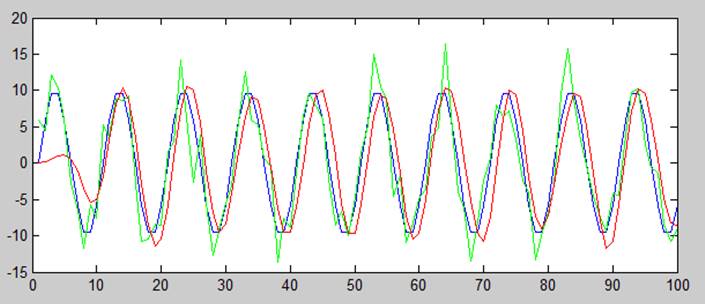
График зависимости амплитуды от времени незашумленного сигнала, зашумленного и отфильтрованного полосовым фильтром с найденными параметрами
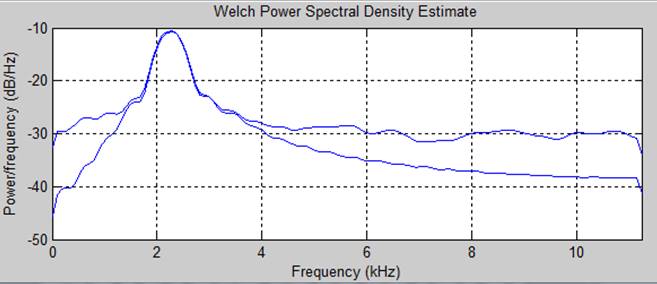
1000-1 Отсчетов(2 случай)
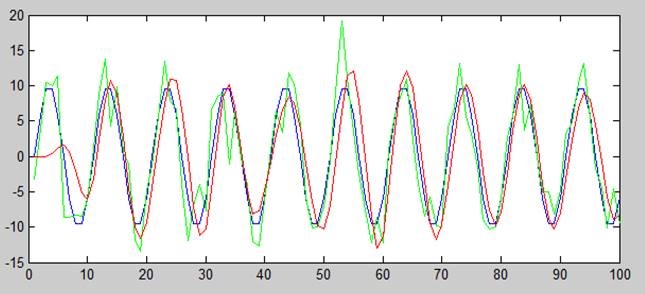
1 случай
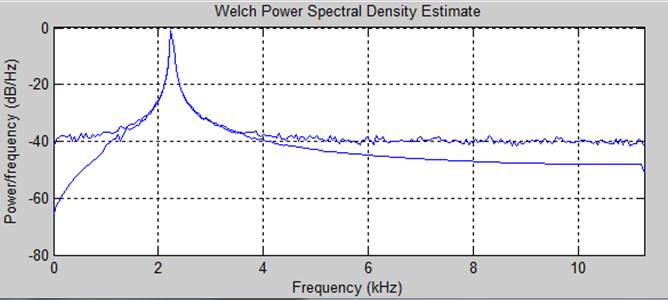
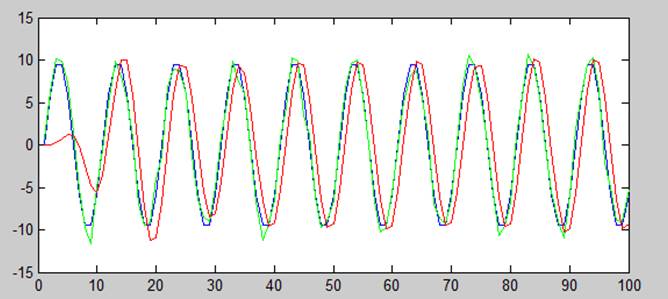
2 случай
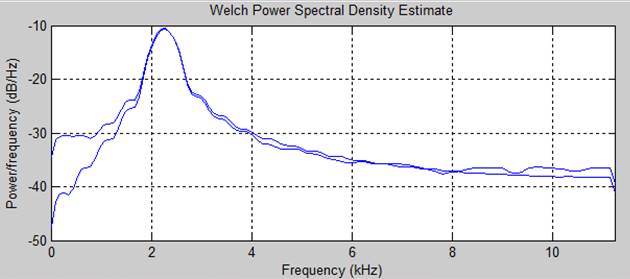
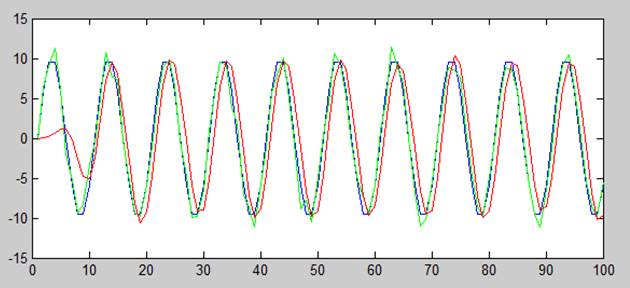
1 случай
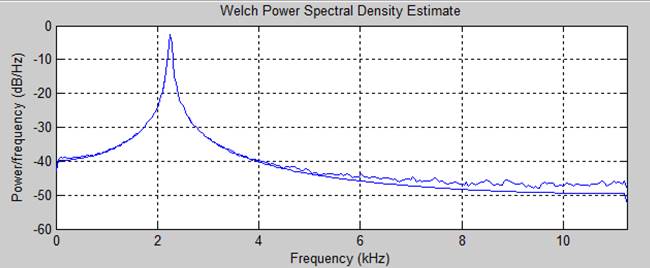
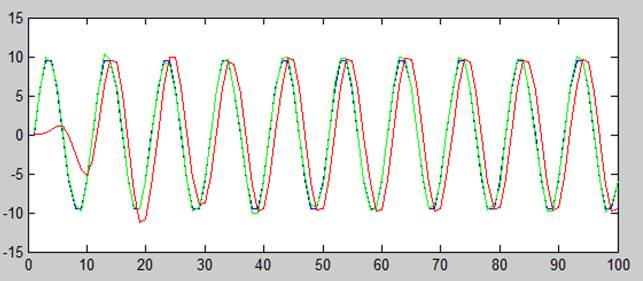
2 случай
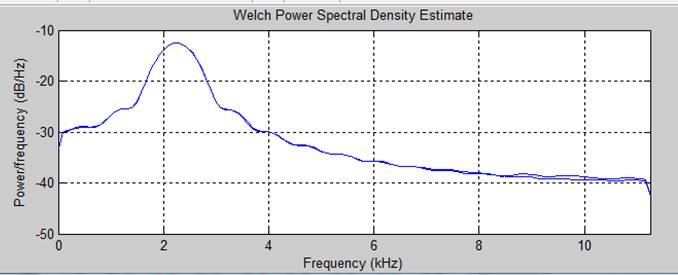
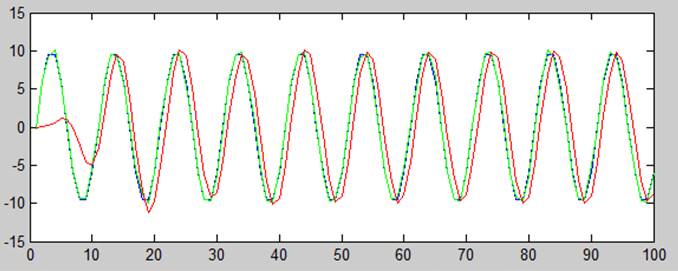
4. Соотношение сигнал/шум -15 дб
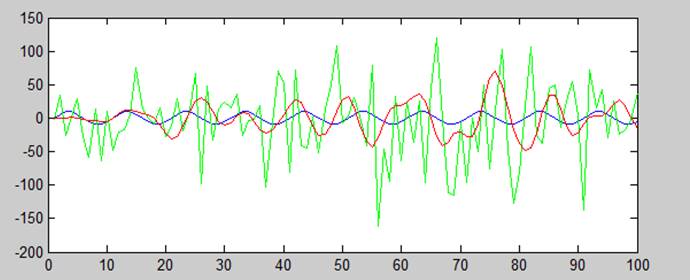
2 случай
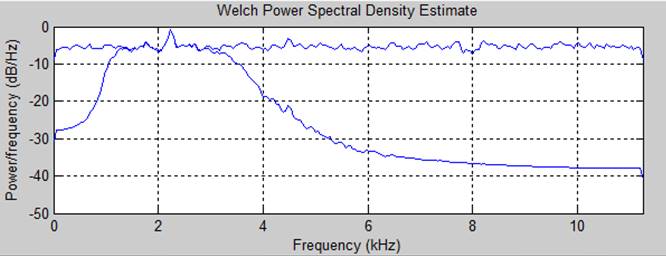
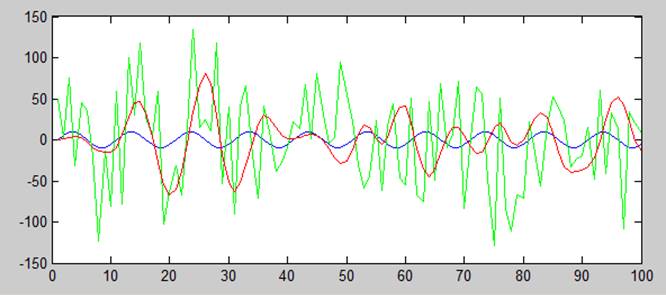
График спектральной плотности мощности с усреднением и без.(на примере 20 дб)
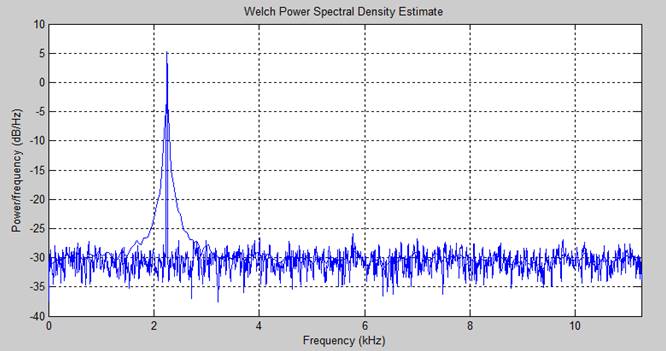
Усреднение велось по 30 точкам
График усреднения по 30 точкам и по 120 на примере сигнал/шум -15 дб
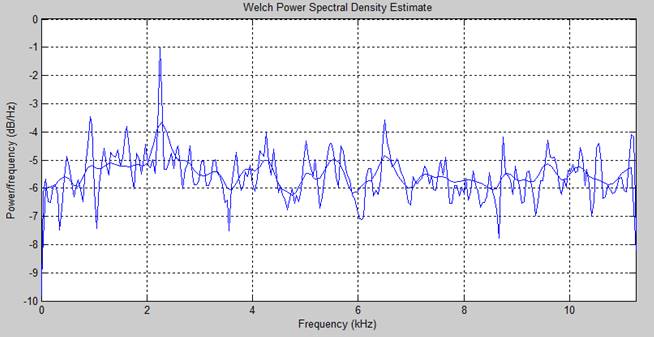
Усреднение позволило нам убрать часть шумов, но пик основной гармоники получился менее выраженным. Это позволяет нам визуально проше определить основную гармонику. По найденному максимуму в спектре были определены пороги пропускания полосового фильтра.
Вывод: Усреднение позволяет лучше определять порог детектирования сигнала как визуально, так и программмно, но может негативно сказаться на широте основной гармоники. Если сигнал далее пропускать через через расчитанный фильтр то лучше не усреднять спектр, так как шумы уберет фильтр а основная гармоника останется неуширенной. Так же если брать сильное усреднение то получившийся спектр станет статистически неустойчив и мы можем построить фильтр по неверным параметрам и непропустить сигнал.
Код программы
Файл lab4.m
clc;
% Commom lab paramaters
fs = 2250; % частота сигнала (гармоническая составляющая);
fd = 22500; % частота дискретизации = 1/ ?t; (из варианта )
N = 10000 -1; % число отсчетов сигнала; (кратно периоду)
dt = 1/fd; % – интервал дискретизации
tBeg = 0;
tEnd = N * dt; % – длина реализации = N * ?t, (интервал наблюдения);
df = fd/N; % разрешение по частоте = Fd / N;
fd/2; % - полоса анализа сигнала
averageCoefficient = 20;
t = (tBeg : dt : tEnd); % формирование времени отсчетов
format long
signalAmplitude = 10;
signalNoize = 10; % в децибеллах
noizeAmplitude = signalAmplitude / 10^(signalNoize/20);
% Гармонический сигнал
harmonySignal = signalAmplitude * sin (2 * pi * fs * t);
% Гармонический сигнал c шумом
harmonySignalWithNoise = harmonySignal + noizeAmplitude * randn(1, N+1);
partToDraw = 100; % Число отсчетов для отрисовки графиков
if(partToDraw > N )
partToDraw = N;
end
%усреднение
[power frequency] = pwelch(harmonySignalWithNoise,[1:N/averageCoefficient],[],[],fd);
pMax = power(1);
for i=1:length(power)
if power(i)>pMax
pMax=power(i);
iMax=i;
end;
end;
pwelch(harmonySignalWithNoise,[1:N/averageCoefficient],[],[],fd);
hold on;
% параматры фильтра
filterOrder = 4; % порядок фильтра;
topFrequency = frequency(iMax)/(fd/2) + 0.1; % относительная частота среза (0.4)
lowFrequency = frequency(iMax)/(fd/2) - 0.1; % нижняя граница среза (0.1)
% фильтрация полосового фильтра
[b,a] = butter(filterOrder,[lowFrequency, topFrequency],'bandpass');
filteredSignal = filter(b, a, harmonySignalWithNoise) ;
pwelch(filteredSignal,[1:N/averageCoefficient],[],[],fd);
figure;
plot(harmonySignal(1:partToDraw));
hold on;
plot(harmonySignalWithNoise(1:partToDraw),'g');
plot(filteredSignal(1:partToDraw),'r');
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.