называется множество центров максимальных шаров, содержащихся в X.

Пример максимального шара показан на Рис. 9. Обозначим через Sr (X), r >
0, r-е скелетное подмножество, т.е. множество центров максимальных шаров радиуса r.
Скелет SK(X) ограниченного открытого непустого множества X ⊂ Rm задается формулой
![]()
Здесь drB – “замкнутый шар бесконечно малого радиуса dr”, а отмыкание множества Y структурирующим элементом drB есть Y ◦ drB = s>0 (Y ◦ sB).
Рассмотрим теперь дискретный случай. Пусть множество X представляет дискретное бинарное изображение из Zm . Будем предполагать, что множество
X является непустым и ограниченным.
Алгоритм Серра построения морфологического скелета SK(X) (или SK(X, B) для большей определенности) дискретного бинарного изображения X структурирующим элементом B имеет вид
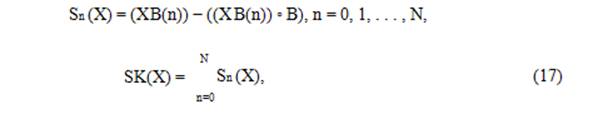
где N = max{n| X B(n) = ∅}. Следует помнить, что скелетные подмножества имеют метки, равные номерам этих подмножеств. Знание номеров скелетных подмножеств позволяет восстанавливать исходное бинарное изображение. Изображение X восстанавливается по скелетным множествам следующим образом

Этот алгоритм является непосредственным аналогом формулы для непрерывного случая.
Очевидно, что различные структурирующие элементы дают различные скелеты, при этом несимметричные структурирующие элементы дают скелеты, которые абсолютно не напоминают осей симметрии объекта. Но каждый скелет содержит достаточно информации для полного восстановления изображения.
На Рис. 10 показаны структурирующие элементы, использованные для построения скелета одного и того же бинарного изображения Рис. 11а).

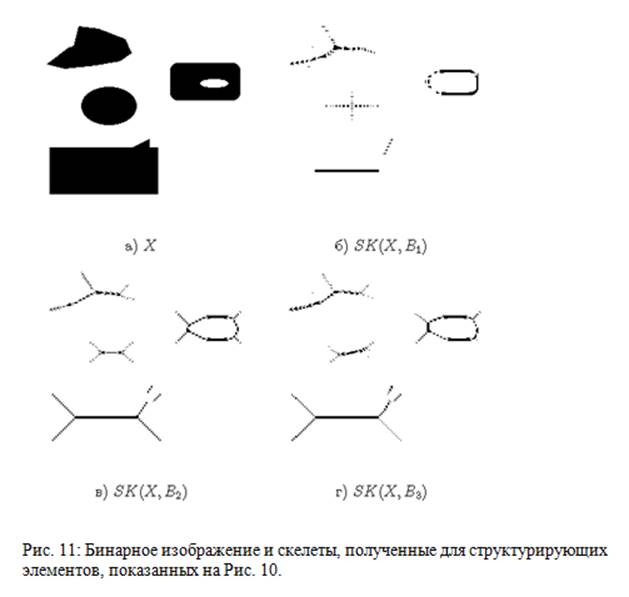
23.3. Свойства морфологического скелета
Предположим, что дискретный структурирующий элемент B содержит начало координат.
1. Если B = {0}, то SK(X) = ∅;
2. Если XB = ∅, то SK(X) = X;
3. Различные скелетные множества Sn (X) не пересекаются;
4. Преобразование получения морфологического скелета является инвариантным относительно сдвига изображения, антиэкстенсивным и идемпотентным.
Последние два свойства справедливы и для непрерывного случая.
Теорема 2 Если скелет изображения X получен с помощью ограниченного выпуклого структурирующего элемента B, то точка z принадлежит n-му скелетному подмножеству Sn (X) тогда и только тогда, когда шар B(n)z является максимальным в X.
Теорема 3 Если скелет изображения X получен с помощью ограниченного выпуклого структурирующего элемента B, то X эквивалентно отмыканию X ◦ kB тогда и только тогда, когда первые k скелетных подмножеств
Sn (X), n = 0, 2, . . . , k − 1 являются пустыми.
6) Морфологический спектр.
24. Морфологический спектр
Одной из важнейших проблем в машинном зрении и обработке изображений является проблема представления формы-размера изображения.
Непрерывные бинарные изображения. Определим спектр компактного бинарного изображения X ⊆ Rm относительно выпуклого бинарного изображения B ⊆ Rm следующим образом:
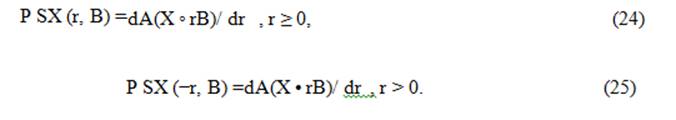
Здесь A(X) – площадь множества X, X ◦ rB – отмыкание множества X структурирующим элементом rB (т.е. элементом радиуса r, если радиус элемента B является единичным),
X • rB – замыкание множества X структурирующим элементом rB.
Выпуклость B гарантирует неотрицательность спектра для всех значений
r ∈ R, т.к. X ◦ rB ⊇ X ◦ sB, если r < s.
Поскольку X – компактное множество, то существует максимальное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.