Решение задач линейного программирования в Excel. Общая характеристика организации решения задач линейного программирования в Excel

2.6 Решение задач линейного программирования в Excel.

2.6.1  Общая характеристика организации решения задач линейного программирования в  Excel.

Рассмотренный в предыдущем параграфе пример свидетельствует о простоте использования алгоритма симплексного метода. Однако, следует заметить, что алгоритм легко и просто реализуется  в небольших по размеру задачах. По мере увеличения их размеров  вычислительные трудности возрастают катастрофически быстро. Решение задачи становится возможным только с помощью компьютера. Это можно отнести к подавляющему большинству задач, имеющих практическую значимость. Применительно к изложенному следует обратить внимание на еще одно важное достоинство рассмотренного алгоритма – простоту его реализации в виде компьютерных программ. Одна из этих программ реализована средствами Excel.

Последовательность работ, выполняемых пользователем при решении задач линейного программирования с помощью этой программы, предоставлена в виде блок-схемы (рис 2.8)

Содержание и последовательность выполнения операций каждого блока, которых требуется участие пользователя, будет рассматриваться на примере задачи планирования производства, математическая модель которой приведена.

2.6.2 Разработка и ввод формы документа для решения задачи.

Созданию формы должно предшествовать планирование размещения исходных и искомых характеристик, обеспечивающее наглядность отображения и удобства проведения анализа результатов решения задачи. С этой целью в формируемый документ может быть включена текстовая информация ( заголовок документа, заголовок отдельных строк и столбцов, пояснения внутри таблицы). Весь текст, включенный в документ, является комментарием и не влияет на решение задачи. Пользователь имеет возможность самостоятельно определить наиболее приемлемую на его взгляд форму выходного документа.

Для выбранной в качестве примера задачи, форма документа может иметь вид ( рис 2.9 ):                                                                       

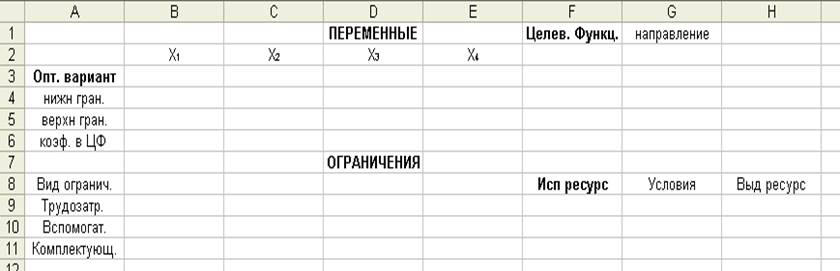
Рис 2.9.

В приведенной форме в строке 2 применительно к рассматриваемой математической модели записываются обозначения искомых переменных. В соответствующих  клетках строки 3 будут представлены их значения в оптимальном варианте решения. Строки 4 и 5 предназначены для записи границ допустимых значений каждой из переменных. Например, если бы возможные значения переменной Х1 находились в диапазоне 1 ≤ Х1≤4, то в клетку В4 следовало ввести 1, а в клетку В5 - 4. Применительно к условиям рассматриваемого примера следует ввести нули в клетки В4 – Е4. Возможно, в таких случаях нули и не записывать, обязательно оставив указанные клетки пустыми. Клетки под переменными в последующих строках заполняются значениями их коэффициентов из уравнений целевой функции и системы ограничений.

При вводе ограничений, в столбце А для большей наглядности записываются наименования видов ограничения, определяющих решение задачи. В столбце Н по каждому виду ограничений из математической модели записывается выделяемый ресурс, а в столбце G указывается условие его использования (для нашего примера это ≤ по всем ограничениям).В клетку G6 целесообразно записать для наглядности направление изменения целевой функции (max, min), о чем указывается в заголовке столбца.

Следует обратить внимание на столбец F, который будет заполнен данными в результате решения задачи. В клетке F6 будет записано значение целевой функции (в клетке F1 приведен соответствующий заголовок). В клетках F9 – F11 будет охарактеризовано использование выделенных ресурсов, соответствующее оптимальному варианту решения задачи.

2.6.3.  Ввод в форму документа искомых данных.

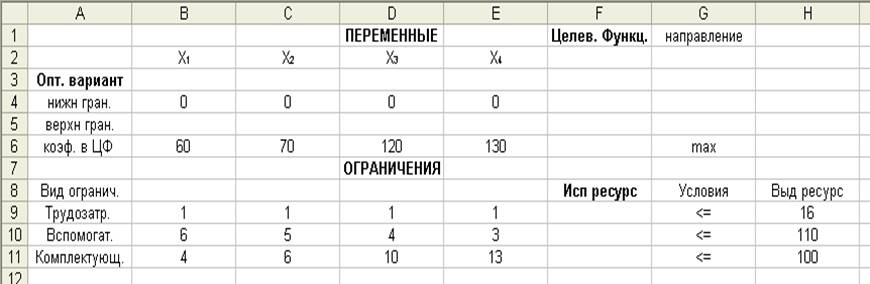
В качестве исходных данных в форму документа вводятся значения коэффициентов при переменных из уравнения целевой функции и системы ограничений. Кроме того для ограничений должны быть введены их свободные члены, а также знаки, определяющие возможность использования выделенных ресурсов. Заполненная искомыми данными форма представлена в табл. 2.10.

Таблица 2.10.                  

2.6.4  Ввод алгоритма решения задачи.

Ввод алгоритма состоит из двух последовательно выполняемых этапов