Структурная схема моделируемой системы управления. Математическое описание исходных данных. Моделируемая система

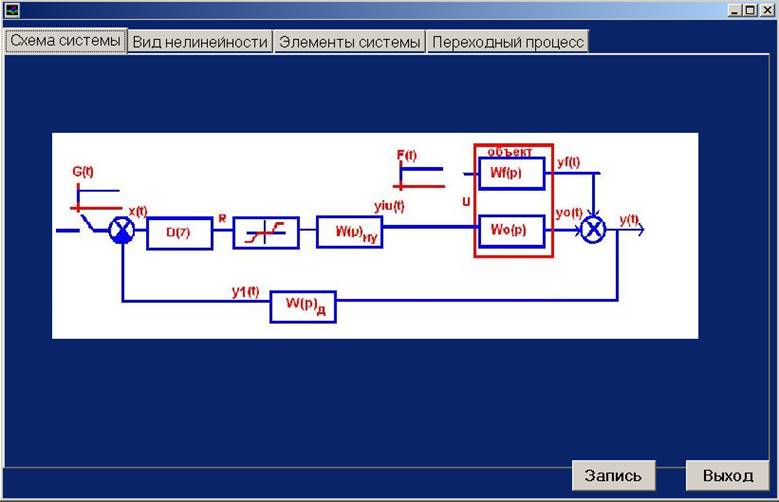
1.  Структурная схема моделируемой системы управления

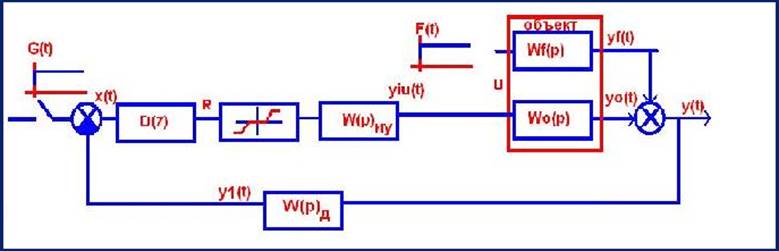
Рис.1. Структурная схема системы.

2.  Математическое описание исходных данных

Моделируемая система

D(z)=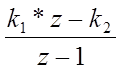 - дискретная передаточная функция ПИ-регулятора;

W_им(р)=k_им – передаточная функция исполнительного механизма;

W_po(p)=k_po – передаточная функция регулирующего органа;

W_o(p)=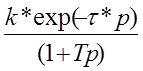 - передаточная функция объекта по каналу управления;

W_д(р)=k_д – передаточная функция датчика;

W_f(p)=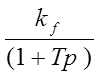 - передаточная функция объекта по каналу возмущения;

W_фэ(p)=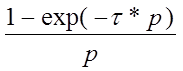- передаточная функция фиксатора нулевого порядка.

A(t)=A*1[t] – сигнал задающего воздействия

A_f(p)=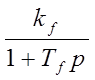 - сигнал возмущения на вход объекта управления

Нелинейный элемент.

В моделируемой системе нелинейная характеристика присутствует в дискретном регуляторе. Вид нелинейности – «реальное ограничение». (рис.2.)

Задана нелинейность дискретного регулятора, которая имеет вид:

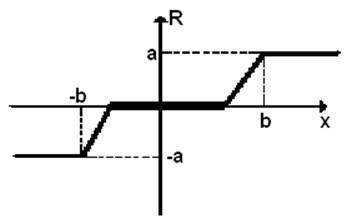
Рис.2. Вид нелинейности – “реальное ограничение”

c:=(b/x[n])+a;

If (R[n]<a) and (R[n]>-a) Then Un[n]:=0;

If R[n]<-a then Un[n]:=(R[n]+a)*Kpo;

If R[n]<-c then Un[n]:=-b;

If R[n]>c then Un[n]:=b;

U[n]:=Kum*Kpo*Un[n]

 

3. Определение дискретной модели непрерывной части системы и

соответствующего разностного  уравнения.

1. Нахождение дискретной передаточной функции объекта управления:

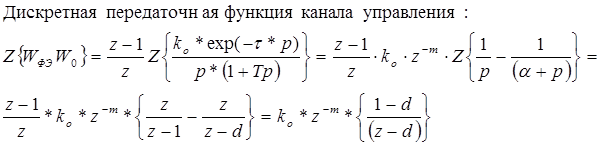
Запишем разное уравнение, которые описывают работу объекта по каналу управления: 

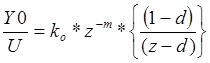
y0[n]=y0[n-1]*d - k0*U[n-m-1]-k0*d*U[n-m-1];

4. Определение непрерывной и дискретной модели нелинейной характеристики заданного элемента системы.

В моделируемой системе нелинейная характеристика присутствует в дискретном регуляторе. Вид нелинейности – «реальное ограничение». (рис.2.)

Задана нелинейность дискретного регулятора, которая имеет вид:

Рис.2. Вид нелинейности – “реальное ограничение”

c:=(b/x[n])+a;

If (R[n]<a) and (R[n]>-a) Then Un[n]:=0;

If R[n]<-a then Un[n]:=(R[n]+a)*Kpo;

If R[n]<-c then Un[n]:=-b;

If R[n]>c then Un[n]:=b;

U[n]:=Kum*Kpo*Un[n]

5.Составление системы разностных уравнений, описывающих работу замкнутой системы управления. Анализ полученной системы уравнений для определения типа и первоначальных значений переменных

Для программирования данной системы необходимо перейти от дискретных функций элементов системы к разностным уравнениям.

1. Получим разностное уравнение для ПИ – регулятора:

y0[n]=y0[n-1]*d - k0*U[n-m-1]-k0*d*U[n-m-1

2. Уравнение возмущения на вход объекта

yf[n]=(cf*kf*(1-exp(-n*Tdis/Tf)))

3.Сумматор

4. Уравнение датчика

4.Сигнал ошибки рассогласования

5 .Уравнение регулятора

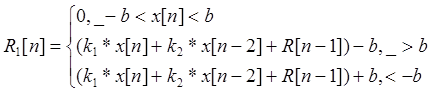
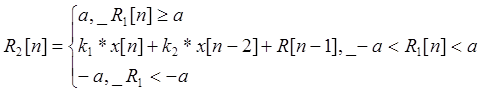
6.Уравнение исполнительного механизма

S[n] = K_им*R[n]

7.Уравнение регулирующего органа

U[n] = K_po*S[n]

Анализируя все переменные, которые присутствуют в цикле, можно сделать вывод, что на все переменные должны задаваться массивом.

определяем в массив, так как используются в расчете их     предыдущее     значение в текущем такте.

n – текущий такт расчета;

y0[n]        

x[n]

U[n]

			Задаем как простые переменные, так как рассчитываются только в текущем такте.

 

yf[n]

y[n]

6.Эскизы формы

Форма имеет четыре закладки:

1. «Схема системы»:

2. «Вид нелинейности»

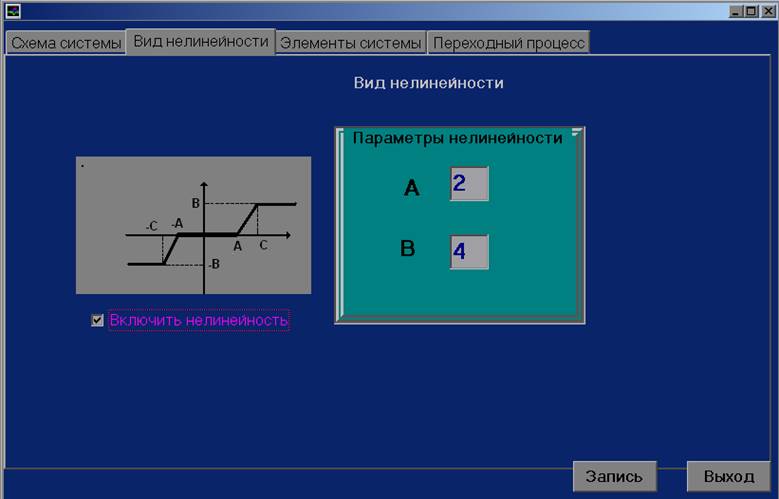
3. «График нелинейности»

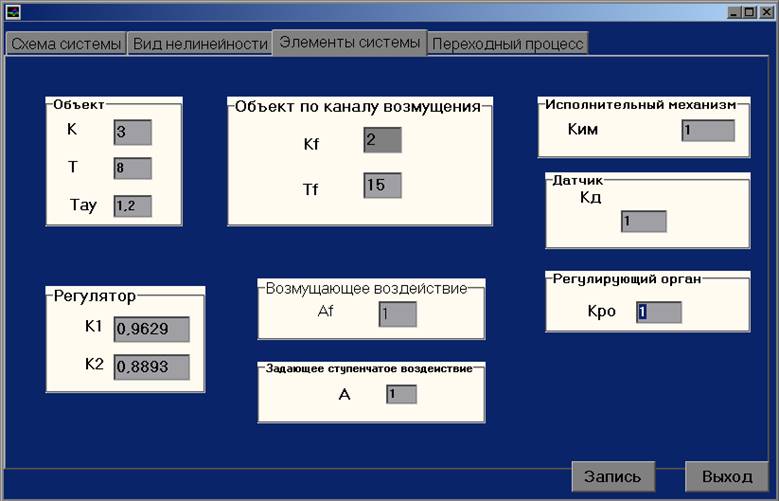
4. «Элементы системы»

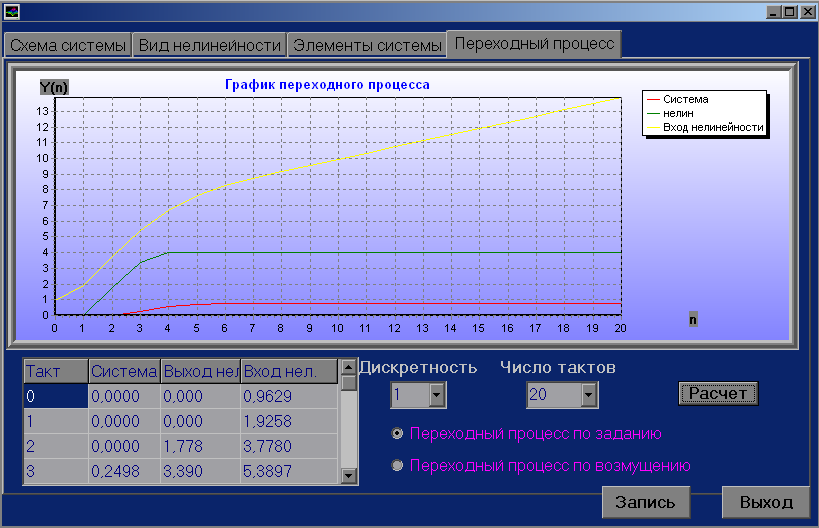
7.Коды программы

procedure TForm1.FormCreate(Sender:TObject);

Begin

With stringgrid2 do

begin

cells[0,0]:='Такт';

cells[1,0]:='Система';

cells[2,0]:='Выход нел.';

cells[3,0]:='Вход нел.';

Rowcount:=2;

end;

End;

procedure TForm1. Edit1Change(Sender: TObject);

Var

N,I:Integer;

Begin

Series1.Clear;

N:=StrToInt(ComboBox3.Text);

For I:=1 to N do

With StringGrid2 do

Begin

Cells[0,0]:='  ';

Cells[1,0]:='  ';

Cells[2,0]:='  ';

Cells[3,0]:='  ';

RowCount:=3;

End;

End;

procedure TForm1.Button2Click(Sender: TObject);

begin

Close;

end;

procedure TForm1.Edit2Change(Sender: TObject);

Var

N,I:Integer;

Begin

Series1.Clear;

N:=StrToInt(ComboBox3.Text);

For I:=1 to N do

With StringGrid2 do

Begin

Cells[0,0]:='  ';

Cells[1,0]:='  ';

Cells[2,0]:='  ';

Cells[3,0]:='  ';

RowCount:=3;

End;

End;

//Расчет системы

procedure TForm1.Button3Click(Sender: TObject);

Var

K1,K2,K,T,Tau,Tdis,Kum,Kpo,Kd,Sig,a,b,c,y,y1,yf,cf,kf,tf,r,un,un0:real;

i,n,m:Integer;

U:array of real;

Yo:array of real;

X:array of real;

Begin

a:=StrToFloat(Edit1.Text);

b:=StrToFloat(Edit2.Text);

K1:=StrToFloat(Edit7.Text);

if k1=0 then

begin

messagedlg('Неправильно введены настройки регулятора: к1',mterror,[mbok],0);

exit;

end;

K2:=StrToFloat(Edit8.Text);

if k2=0 then

begin

messagedlg('Неправильно введены настройки регулятора: к2',mterror,[mbok],0);

exit;

end;

K:=StrToFloat(Edit9.Text);

if k=0 then

begin

messagedlg('Неправильно введены параметры объекта: к',mterror,[mbok],0);

exit;

end;

Tau:=StrToFloat(Edit10.Text);

if tau=0 then

begin

messagedlg('Неправильно введены параметры объекта: тау',mterror,[mbok],0);

exit;

end;

t:=strtofloat(edit13.Text);

if t=0 then

begin

messagedlg('Неправильно введены параметры объекта: Т',mterror,[mbok],0);

exit;

end;

kf:=strtofloat(edit3.text);

Tf:=strtofloat(edit4.text);

Cf:=strtofloat(edit14.text);

Kum:=StrToFloat(Edit5.Text);

if Kum=0 then

begin

messagedlg('Неправильно введены параметры системы: Ким',mterror,[mbok],0);