Идентификация объекта. Синтез цифровых регуляторов. Программирование в пакете «Intouch.16»

Министерство образования Российской Федерации

Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров

 

Кафедра автоматизированного электропривода и электротехники

дисциплина: «Цифровые системы автоматического управления» и «Микропроцессорные средства в электроприводе»

Пояснительная записка

Выполнили: Студенты V-курса

            группы № 3

              специальности 180400__________ / /

                                         __________ / /

Проверил: к.т.н.; доцент

кафедры «АЭ и Э»______________ / /

Санкт-Петербург

2001 г.

Содержание.

1. Идентификация объекта.-------------------------- 3стр

2. Синтез цифровых регуляторов.-------------------- 7стр

3. Программирование в пакете «Intouch.16».--------- 10стр

1. Идентификация объекта.

Задачей данной работы является идентификация передаточной функции в цифровом виде  по заданному непрерывному переходному процессу.

Рассмотрим любой непрерывный переходный процесс, передаточная функция которого имеет вид:          W (S) = (0.11s+1) / (0.005s² + 0.048s +1);

Переходный процесс представлен на Рис.1.1

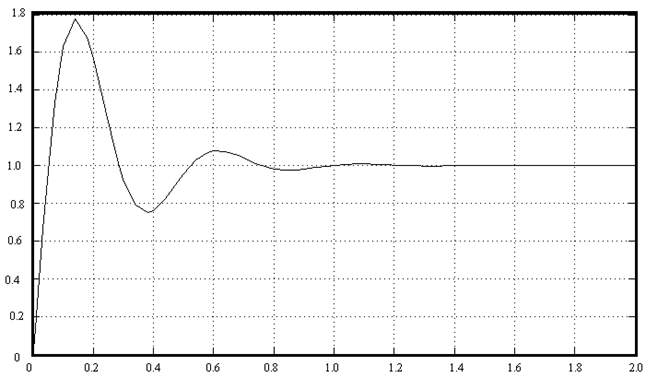Рис.1.1 Заданный переходный процесс.

Для идентификации передаточной функции объекта в цифровом виде необходимо снять точки для создания решетчатой функции. Через интервал времени 0,1с снимаем значения (Y). Ниже в таблице №1 приведены значения.

Таблица№1.

t	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
с	0	1,57	1,55	0,93	0,78	0,95	1,08	1,04	0,99	0,99	1

1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
1,008	1,003	0,997	1	1	1	1	1	1	1

Y(z) = C₀z⁰ + C₁z^-1 + C₂z^-2 +…+ C_kz^-k,                                                         (1)

С другой стороны, формулу (1) можно представить в виде:

Y(z) = C₀z⁰ + C₁z^-1 + C₂z^-2 +…+ C_kz^-k =

b₀ + b₁z^-1 + … + b_mz^-m

= ———————————                                                                     (2)

a₀ + a₁z^-1 + … + a_m+1z^-(m+1)

где: b₀ = 0;  a₀ = 1;

c_i – коэффициенты ряда Лорана;

m – степень характеристического уравнения замкнутой цифровой системы, причем m<k;

k – число интервалов квантования, необходимых для вхождения дискретной переходной характеристики.

Для определения коэффициентов а и b необходимо создать массив из выборки значений непрерывной переходной функции  с  к =10.

Массив {Y} создан в пакете MATLAB и представлен ниже:

С_i =[1.57 1.55 0.93 0.78 0.95 1.08 1.04 0.99 0.99 1 1.008 1.003 0.997 1 1 1 1 1 1 1];

C_i = y_i

Y1=[-y(10) -y(9) -y(8) -y(7) -y(6) -y(5) -y(4) -y(3) -y(2) -y(1)

-y(11) -y(10) -y(9) -y(8) -y(7) -y(6) -y(5) -y(4) -y(3) -y(2)

-y(12) -y(11) -y(10) -y(9) -y(8) -y(7) -y(6) -y(5) -y(4) -y(3)

-y(13) -y(12) -y(11) -y(10) -y(9) -y(8) -y(7) -y(6) -y(5) -y(4)

-y(14) -y(13) -y(12) -y(11) -y(10) -y(9) -y(8) -y(7) -y(6) y(5)

-y(15) -y(14) -y(13) -y(12) -y(11) -y(10) -y(9) -y(8) -y(7) -y(6)

-y(16) -y(15) -y(14) -y(13) -y(12) -y(11) -y(10) -y(9) -y(8) -y(7)

-y(17) -y(16) -y(15) -y(14) -y(13) -y(12) -y(11) -y(10) -y(9) -y(8)

-y(18) -y(17) -y(16) -y(15) -y(14) -y(13) -y(12) -y(11) -y(10) -y(9)

-y(19) -y(18) -y(17) -y(16) -y(15) -y(14) -y(13) -y(12) -y(11) -y(10)];

Далее представим матрицу  {В}

b=[y(11)

y(12)

y(13)

y(14)

y(15)

y(16)

y(17)

y(18)

y(19)

y(20)];

Произведём вычисление коэффициентов – {а} по формуле:

a=y1^(-1)*b и проверим правильность вычисления: сумма полученных коэффициентов должна равняться нулю.

Σa=1+a(1)+a(2)+a(3)+a(4)+a(5)+a(6)+a(7)+a(8)+a(9)+a(10)=0

Результат представлен ниже

a =     -0.8748

0.6162

-0.2522

-0.1894

-0.0973

-0.1186

-0.0180

-0.0599

-0.0031

-0.0027

Сумма коэффициентов равна    Σa =  1.5038e-004

Как видно, сумма стремится к нулю.

Теперь опредилим коэффициенты - {b} по формулам

b1=y(1)

b2=y(2)+a(1)*y(1)

b3=y(3)+a(1)*y(2)+a(2)*y(1)

b4=y(4)+a(1)*y(3)+a(2)*y(2)+a(3)*y(1)

b5=y(5)+a(1)*y(4)+a(2)*y(3)+a(3)*y(2)+a(4)*y(1)

b6=y(6)+a(1)*y(5)+a(2)*y(4)+a(3)*y(3)+a(4)*y(2)+a(5)*y(1)

b7=y(7)+a(1)*y(6)+a(2)*y(5)+a(3)*y(4)+a(4)*y(3)+a(5)*y(2)+a(6)*y(1)

b8=y(8)+a(1)*y(7)+a(2)*y(6)+a(3)*y(5)+a(4)*y(4)+a(5)*y(3)+a(6)*y(2)+a(7)*y(1)

b9=y(9)+а(1)*y(8)+a(2)*y(7)+a(3)*y(6)+a(4)*y(5)+a(5)*y(4)+a(6)*y(3)+a(7)*y(2)+

a(8)*y(1)

b10=y(10)+a(1)*y(9)+a(2)*y(8)+a(3)*y(7)+a(4)*y(6)+a(5)*y(5)+a(6)*y(4)+a(7)*y(3)+a(8)*y(2)+a(9)*y(1)

Результат приведён ниже

B =           b0=0  b1 =1.5700   b2 =0.1766   b3 =0.5415   b4 =0.5256   b5 =0.1524

b6 =0.0487   b7 =-0.0293   b8 =0.0557   b9 =0.0043   b10 =-0.0223