Идентификация объекта. Синтез цифровых регуляторов. Программирование в пакете «Intouch.16», страница 2

Для окончательного получения коэффициенты {a} для передаточной функции в цифровом виде необходимо их пересчитать по формулам:

d0=1;	d0=1.0000
d1=a(1)+d0;	d1=0.1252
d2=a(2)+d1;	d2=0.7414
d3=a(3)+d2;	d3=0.4892
d4=a(4)+d3;	d4=0.2998
d5=a(5)+d4;	d5=0.2025
d6=a(6)+d5;	d6=0.0839
d7=a(7)+d6;	d7=0.0658
d8=a(8)+d7;	d8=0.0059
d9=a(9)+d8;	d9=0.0028
d10=a(10)+d9;	d10=0.0002

Представим передаточную функцию объекта в цифровом виде:

Переходный процесс представлен на рис.1.2

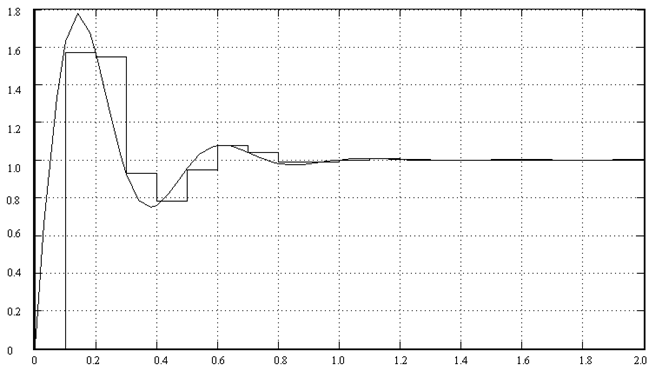Рис.1.2 Переходный процесс идентифицированной цифровой передаточной функции объекта.

Рис.1.2 подтверждает правильность расчёта идентификации передаточной функции в цифровом виде  по заданному непрерывному переходному процессу.

Далее рекомендуется сократить степень полиномов передаточной функции в цифровом виде.

2. Синтез цифровых регуляторов.

Возьмём непрерывную САР контура скорости привода постоянного тока ПРС, из курсовика по дисциплине “СУЭП” (Козярук А. Е.), настроенную на симметричный оптимум.

САР контура скорости представлена на Рис .2.1

Рис.2.1 Структурная схема контура скорости.

Переходный процесс непрерывной системы представлен на рис.2.2

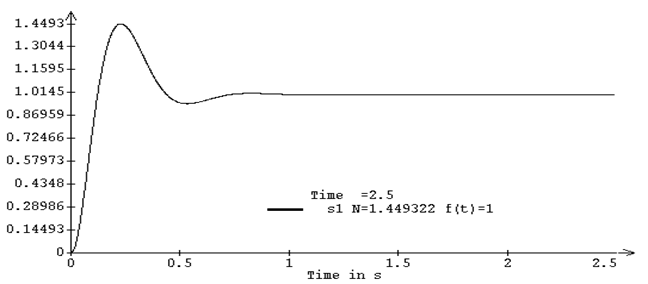Рис.2.2 Переходный процесс контура скорости по заданию.

В общем случае передаточная функция микроконтроллера (или дискретного фильтра) может быть представлена дробно-рациональным выражением

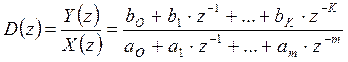
где     Y(z) – изображения решетчатой функций на выходе дискретного фильтра;

X(z) – изображение решетчатой функций на входе дискретного фильтра;

m ³ k.

Регулятор тока и скорости.

Определим уравнение дискретного фильтра для регуляторов тока и скорости. Сначала осуществим z – преобразование передаточной функции регуляторов по методу Тастина.

Передаточная функция регуляторов  тока и скорости

;

;----тогда, воспользовавшись подстановкой получаем

;

После преобразований окончательно получаем

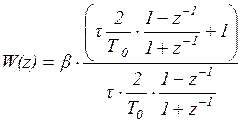
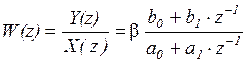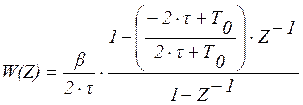где:   ;

;

 ;

 .

После вычислений получили передаточные функции регуляторов вида:

Подставив полученные передаточные функции регуляторов в цифровом виде соответственно получаем цифровую САР контура скорости.

Цифровая САР контура скорости представлена на Рис.2.3.

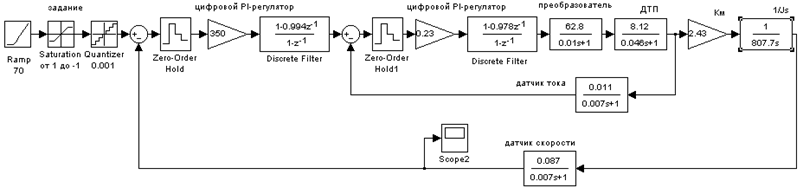Рис.2.3 Цифровая САР контура скорости

Сравним переходный процесс контура скорости по заданию непрерывной и цифровой систем.

Переходные процессы представлены на Рис.2.4

Рис.2.4 Переходный процесс контура скорости по заданию непрерывной и цифровой систем.

Графики переходных процессов, как видно из Рис2.4, почти совпадают, следовательно, метод Тастина для выполнения Z-преобразований непрерывных регуляторов применим для данной САР.

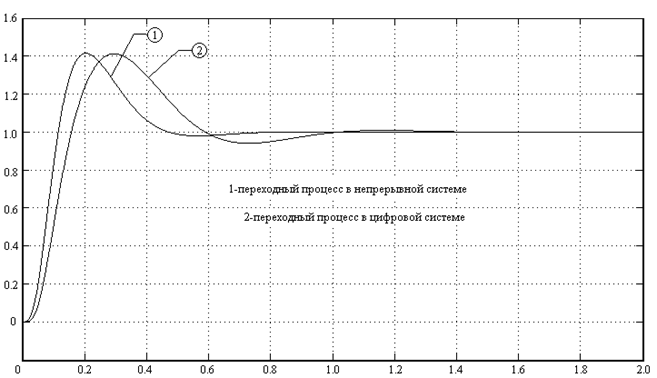Время переходного процесса в цифровой системе задаётся сигналом «RAMP», уровень задания - «SATURATION».

3. Программирование в пакете «Intouch.16».

Задачей являлось ознакомление и программирование в пакете «Intouch.16».

Алгоритм работы:

·  Создание собственного файла;

·  Выбор объектов управления из библиотеки пакета:

1.  Кнопка «Start - Stop» и индикаторы состояния.

2.  Панель регулирования задания «Slider».

·  Выбор объектов, отображающих состояние:

1.  Панель «Meter» со шкалой  и индикаторы состояния.

2.  Создание трендов.

·  Написание скриптов для связи выбранных объектов и выполнения программы.

Скрипты написаны таким образом, чтобы данная система работала следующим:

§  при нажатии кнопки «Start - Stop» загорается индикатор, сигнализирующий о включении системы и разрешающий задавать задание

§  задание задаётся панелью регулирования задания «Slider»

§  задание отображается на двух панелях «Meter»

§  при достижении первой величиной заданного значения мигает индикатор №1

§  при достижении второй величиной заданного значения мигает индикатор №2

§  при достижении первой величиной максимального значения происходит выключение кнопки «Start - Stop» и задавать задание будет возможно лишь при повторном нажатии кнопки «Start - Stop».

Скрипты представлены ниже:

Tagname: pusk

On label: START

Off label: STOP

Expression: pusk

Tagname: Upravl

Pusk= =0

Upravl = 0;

Velichina1=Upravl - 10;

Velichina2=Upravl - 20;

Expression: velichina1>100

Blink when: pusk

Expression: velichina2>50

Blink when: pusk

Velichina1>120

Pusk=0;

Для отображения состояния двух величин представлен тренд, на котором представлены две величины «velichina1» и «velichina2», а также два статических сигнала со значением 50 и 100, при превышении которых происходит мигание индикаторов.