Математическая модель перехода к переменным состояния. Текст программы

Балтийский Государственный Технический  Университет

 им. Д.Ф.Устинова  “Военмех”

Кафедра И3

Отчет по домашней работе №1

Студент группы  И301:

Преподаватель:

Санкт-Петербург

2002 год

Данные: T=RC=1 c.                       Схема:

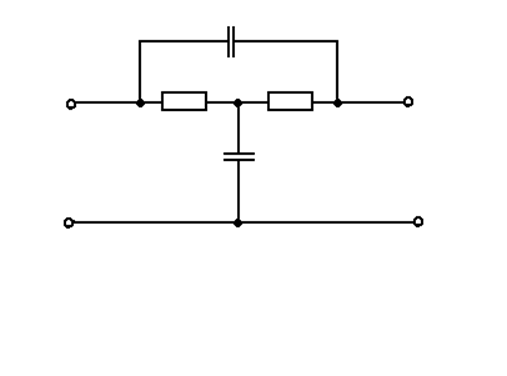
1. Составим математическую модель, переходя к переменным состояния:

X=[U_c1;U_c2]

Узел 1 : I₁=I₂+I_R1

                       I₁=C₁*dx₁/dt=C₂*dx₂/dt+I_R1 (1)

Уравнение выхода : y=u-x₂

I_R1=U₂/R₂=(U₁-x₁-x₂)/R

Из (1) : C₁*dx₁/dt=(U₁-x₁-x₂)/R₂+(U₁-x₁)/R₁ где U₁-x₁-x₂=I₂ а U₁-x₁=I_R1

C₂*dx₂/dt=(U₁-x₁-x₂)/R₂

Подставив T=R*C=1 c получим систему :

Tx₁=-2x₁-x₂+2u

Tx₂=-x₁-x₂+u

y=-x₂+u

2. Записывая в матричном виде систему дифференциальных уравнений, получим :

EX=AX+Bu

y=CX+Du                                      ,где

E=[T,0;0,T],  A=[-2,-1;-1,-1],  B=[2;1],  C=[0,1] и D=1

3. В MatLab`е, используя ControlSystemToolbox получим описание математической модели в виде передаточной функции ( в tf-форме и zpk-форме), а так же АЧХ, ФЧХ, ЛАХ, ЛФХ, АФХ, график переходного процесса U_вых(t) при единичном воздействии вида U_вх=1(t) для данной математической модели.

4. Текст программы (файл 'tay.m') :

%домашнее задание. файл tay.m

clc;

clear;

close all;

T=1;

A=[-2,-1;-1,-2];;

B=[2;1];

C=[0,-1];

D=1;

E=[T,0;0,T];

dss_model=dss(A,B,C,D,E);

tf_model=tf(dss_model)

zpk_model=zpk(dss_model)

[num,den]=tfdata(dss_model,'v');

[mag,phase,w]=bode(num,den);

[y,t]=step(dss_model);

l=length(t);

for i=l:-1:1

if abs(y(l)-y(i))>0.05*abs(y(1)-y(l))

tp=t(i);     break

end

end

fprintf('Продолжительность переходного процесса= %6.2f секунд.\n',tp)

hmax=0;

hmin=0;

for i=1:l

if y(i)>hmax;         hmax=y(i);     end

if y(i)<hmin;          hmin=y(i);     end

end    

sigma=(hmax-hmin-abs(y(l)-y(1)))*100/abs(y(l)-y(1));

fprintf('Перерегулирование системы= %6.2f процентов.\n',sigma)

disp(' ');

disp('Чтобы вывести графики необходимо нажать клавишу "Enter"');

pause;

%Построение АЧХ,ФЧХ

subplot(2,2,2);

plot(w,mag);

grid;

title('АЧХ');

xlabel('\omega,1/c');

ylabel('A(\omega)');

subplot(2,2,4);

plot(w,phase);

grid;

title('ФЧХ');

xlabel('\omega,1/c');

ylabel('\phi\circ(\omega)');

%Построение ЛАХ,ЛФХ

subplot(1,2,1);

bode(dss_model,w)

%Построение АФХ

%График Uвых(t) при Ud[(t)=1(t)

figure;

subplot(1,2,1);

polar(phase*pi/180,mag);

subplot(1,2,2);

step(dss_model);

grid;

5. Графики АЧХ, ФЧХ, ЛАХ, ЛФХ, АФХ и переходного процесса :

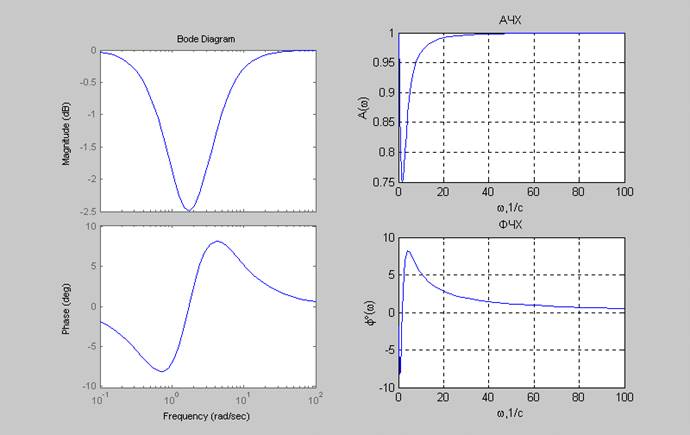
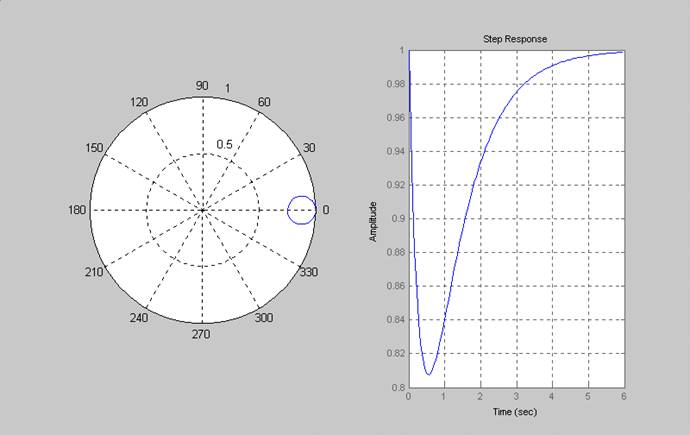
6. Результат программы :

Transfer function:

s^2 + 3 s + 3

------------s^2 + 4 s + 3

Zero/pole/gain:

(s^2 + 3s + 3)

-------------(s+3) (s+1)

Продолжительность переходного процесса=   5.91 секунд.

Перерегулирование системы= 1.28 процентов.

Вывод :

Анализируя вид ПФ и переходного процесса можно сделать выводы, что :

Звено относится к колебательным и при единичном воздействии его перерегулирование δ=1.28%, а время запаздывания t_п=5.91 сек для окрестности Δ=0.05.