Математическая модель, обеспечивающая получение оптимального решения анализируемой задачи

Санкт- Петербургский Государственный Технологический Университет Растительных Полимеров

Кафедра АТЭП

Курсовая работа

по дисциплине:

«Основы теории принятия решений».

Выполнила:                                                               студентка гр. 544            

                                                                                                                                                 

Проверил:                                                                     

Санкт- Петербург

                                                    2008.

Содержание:

Задание на курсовую работу……………………………………………...3

Расчетная часть…………………………………………………………….4

Задание № 15

Построить математическую модель, обеспечивающую получение оптимального  решения анализируемой задачи. Получить оптимальное решение относительно заданного варианта исходных данных.

Постановка задачи .

На предприятии планируется выпуск 2 видов продукции для производства, которых используется 3 компонента. Удельные расходы компонентов на выпуск единицы продукции, запасы компонентов, планируемый обязательный выпуск продукции по видам и прибыль от реализации единицы продукции, приведены в таблице 1.

 

Прод. Комп.	П1	П2	Наличие компонентов
К1	11	7	490
К2	10	6	540
К3	10	12	500
Планируемый выпуск,ед.
Прибыль от ед. продукции	15	18

Таблица 1.

Требуется составить план выпуска продукции, обеспечивающий максимальную прибыль предприятия.

Расчет.

Обозначим через  , количество выпускаемой продукции i-ого вида(i=1,2).

Математическая модель.

Ограничения:

- по   выпуску продукции 2-ого вида

- по количеству компонентов

Уравнение целевой функции:

Исходя из постановки задачи, целевая функция стремиться к максимуму:

         max

Исходные данные  введем  в таблицу  Excel (Таблица 2).

	переменные		целев.функц.	направление
	X1	X2
оптим.вариант
нижняя.граница.	0	30
коэф. В ЦФ	15	18	0	max
	ограничения
			исп.ресурс	условия	выд ресурс
по  компоненту К1	11	7	0	<=	490
по   компоненту К2	10	6	0	<=	540
по  компоненту К3	10	12	0	<=	500

Таблица 2.

Введем математическую модель решаемой задачи.

Вводим зависимость для вычисления значения целевой функции:

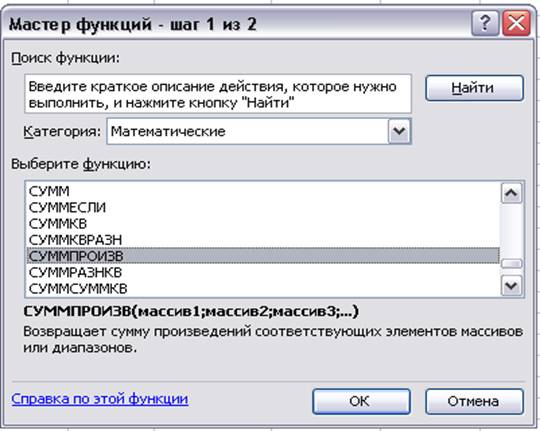
Рис.1 ”Мастер функций”

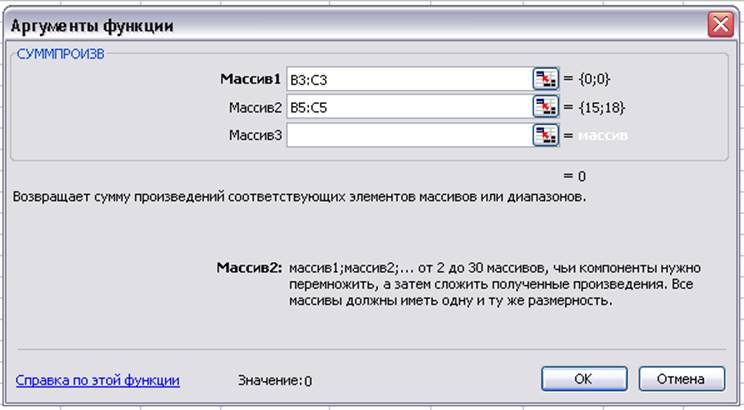
Рис. 2  Диалоговое окно “Аргументы функции”

Далее продолжаем работу в диалоговом окне “Поиск решения”(Рис.3)

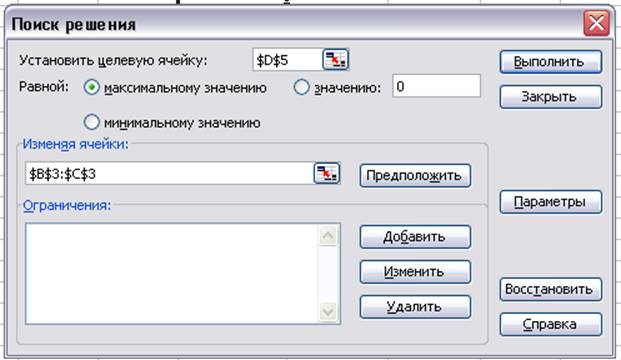
Рис.3 Диалоговое окно “Поиск решения”

Вводим граничные условия на переменные в диалоговом окне “Добавление ограничения”(Рис.4)

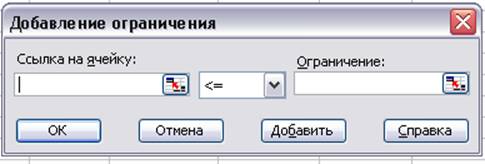
Рис.4 Диалоговое окно “Добавление ограничения”

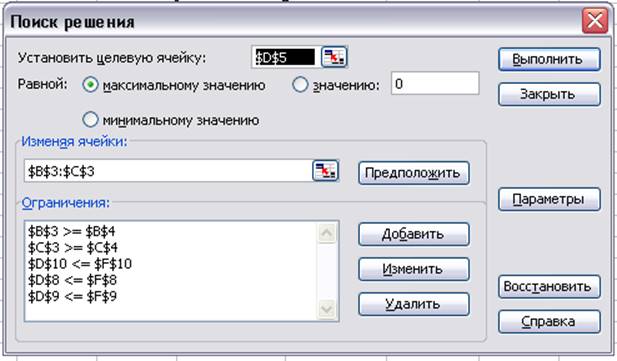
Рис5.Диалоговое окно”Поиск решения” (после введения всех граничных условий).

Управление решением задачи

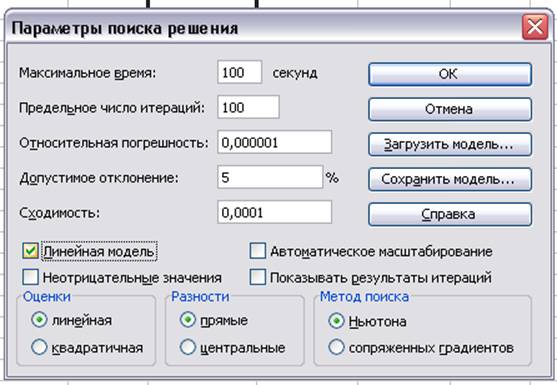
Рис 6.Диалоговое окно”Параметры поиска решения”

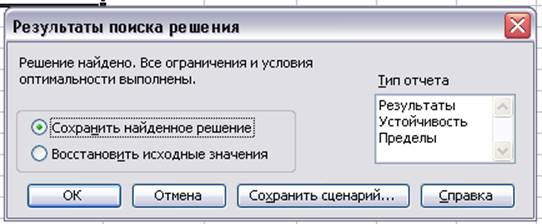
Рис7.Диалоговое окно”Результаты поиска решения”

Полученные результаты выводятся в таблице Excel (Таблица 3):

	переменные		целев.функц.	направление
	X1	X2
оптим.вариант	5,737705133	36,88524572
Нижняя граница	0	30
коэф. В ЦФ	15	18	750	max
	ограничения
			исп.ресурс	условия	выд ресурс
по компоненту К1	11	7	321,3114765	<=	490
по компоненту К2	10	6	278,6885257	<=	540
по компоненту К3	10	12	500	<=	500

Таблица 3.

Полученное  оптимальное  решение  невозможно так, как в результате вычислений оно получилось нецелочисленным, это не является приемлемым для данной задачи.

Получаем целочисленный вариант решения с помощью самостоятельного подбора значений   и   и получаем соответствующие значение целевой функции и используемых ресурсов.

Берем значения  и  ,  и  и  пересчитываем  уравнение целевой функции и ограничения для  целочисленных решений.

1)  и

, 314490

,272540

,494500

2)  и

,314490

,272540

,494500

В результате  расчета получаю, что целевая функция имеет наибольшее значение при  и

Вывод:

В результате расчета, оптимальным вариантом решения в данной задаче  является количество выпускаемой продукции первого вида равное 5,и количество выпускаемой продукции второго вида равное 37 при которых обеспечивается максимальная прибыль предприятия z =741