Идентификация модели по данным пассивного эксперимента в системе “ASIM” раздел ‘IDEN’. Оценка точности экспериментальных данных, страница 2

Генеральное математическое ожидание           каждого коэффициента b_i равно 0.

1.2  Формулируем двустороннюю альтернативную гипотезу:

Н₁:

Генеральное математическое ожидание            каждого коэффициента b_i не равно 0. Значит его значение либо больше 0, либо меньше 0.

2. Задаёмся уровнем ошибки первого рода.

= 0,05;

3. t-статистика.

f = N – L; где N-число опытов;

L-число коэффициентов в модели;

Для первой модели:

f = 23 – 6 = 17;

По таблице распределения Стьюдента при          = 0,05 определяем критическое значение t-статистики:

t_кр = 2,11;

Для второй выборочной модели:

f = 23 – 4 = 19;

t_кр = 2,09;

Если значение t-статистики t_bi  > t_кр  принимаем альтернативную гипотезу и коэффициент модели обозначаем значимым.

Если значение t-статистики t_bi < t_кр принимаем нулевую гипотезу и коэффициенты модели обозначаем незначимыми.

Статические характеристики оценок коэффициентов первой модели.

Таблица №4.

№	Коэффициенты модели	Т-статистика	Оценка
1	b0 = 9.645	tbo = 7.229	значим
2	b1 = 1.051	tb1  = 1.117	незначим
3	b2 = 1.440*10-1	tb2 = 1.569*10-1	незначим
4	b11 = -9.602*10-2	tb11 = 1.217*10-1	незначим
5	b22 = 1.423	tb22 = 1.886	незначим
6	b12 = -8.603*10-5	tb12 = 9.402*10-5	незначим

Статические характеристики коэффициентов выборочной модели.

Таблица №5.

№	Коэффициенты модели	Т-статистика	Оценка
1	b0 = 10,16	tbo = 11,37	значим
2	b1 = 1,060	tb1  = 1,129	незначим
3	b2 = 1,549	tb2 = 1,629	незначим
4	b12 = -2,413	tb12 = 2,603*10-4	незначим

Этап 4:Оценка адекватности модели данным эксперимента.

Для проверки адекватности модели данным эксперимента осуществляется сравнение разброса опытных данных относительно выбранной модели с точностью экспериментальных данных, которые определяются по результатам параллельных опытов.

Точность экспериментальных данных оценивается дисперсией воспроизводимости           _воспр и числом степеней свободы f_воспр .

_воспр = (       _1выбр * f₁ +         _2выбр * f₂)/(f₁ + f₂);

_воспр = (0,0310005² * 1 = 0,0508805² * 1)/(1 + 1) = 0,00609956

Точность модели относительно данных эксперимента оценивается остаточной дисперсией               _ост  и числом степеней свободы f_ост .

Для первой модели:         _ост = 14,22;

f_ост = 23 – 6 = 17;

Для выборочной модели:         _ост = 17,93;

f_ост = 23 – 4 = 19;

 

1.1Формулируем нулевую гипотезу:

Н₀:         

Генеральное значение точности модели  и генеральное значение точности экспериментальных данных равны, т.е. различия полученные в опыте – случайны.

1.2 Формулируем альтернативную гипотезу:

Н₁:

Генеральное значение точности модели  больше генерального значения точности экспериментальных данных равны.

2. Задаёмся уровнем ошибки первого рода.

= 0,05;

3. F-статистика.

Для первой модели:

F_расч =         _ост /        _воспр = 14,22/0,0060995 = 2331,3386;

f₁ = 17;

f₂ = 2;

По таблице распределения Фишера: F_кр = 19,35;

Для выборочной модели:

F_расч =         _ост /        _воспр = 17,93/0,0060995 = 2939,5859;

f₁ = 19;

f₂ = 2;

По таблице распределения Фишера: F_кр = 19,45;

 

Если F_расч > F_кр  - принимаем альтернативную гипотезу.

Это означает, что и первая, и вторая выборочная модели не адекватны данным эксперимента. Расхождение между дисперсиями не случайно.

Этап 5:Корреляционный анализ модели статики.

Поле корреляции:

График №1.

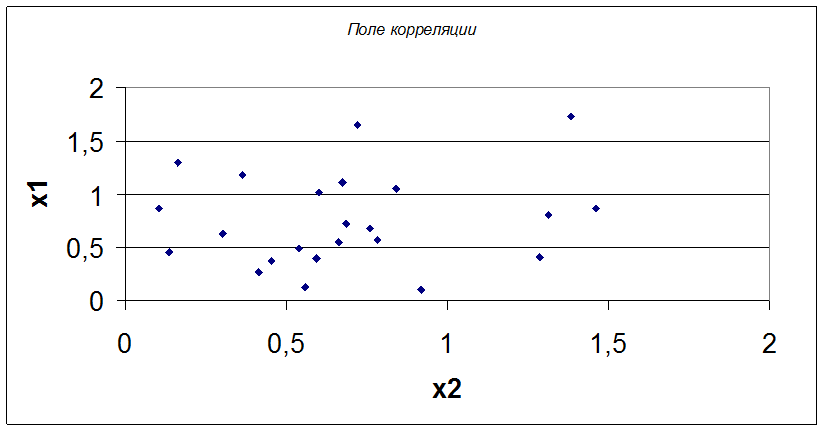
Количественная оценка корреляционной связи определяется по корреляционному моменту:

R_xx = М{XX} = где ХХ – центрированные значения;

r_xx  = 1;

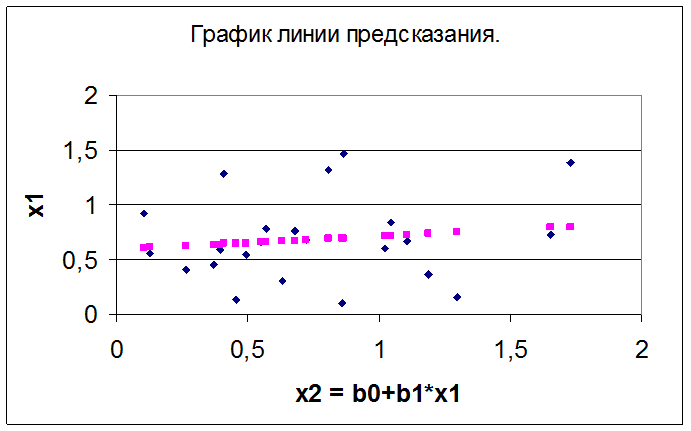
График линии предсказания:                                           График №2.

Связь между двумя случайными величинами Х₁ и Х₂ оформлена в виде нормированной корреляционной матрицы входных переменных.

Таблица №6.

	Х1	Х2
Х1	1	0,154
Х2	0,154	1

r_xx  = 1 => между Х₁  и Х₂ существует функциональная связь – самая сильная.

Сила связи – максимальная.

Зависимость – линейная.

Уравнение линии предсказания в общем виде будет:

Х₂ = b₀ +b₁*X₁ , где

b₁ = r_xx *

b₁ = 0.154*(0.14947/0.19301) = 0.11926;

b₀ = m_x2 – b₁* m_x1;

b₀ = 0.6837-0.11926*0.75443 = 0.5938067;

Х₂ = 0.593806 + 0.11926*X₁;

Вывод: Входные переменные Х₁ и Х₂ являются независимыми между собой случайными величинами, имеющие нормальный закон распределения.

Выходные переменные также независимы друг от друга в каждом опыте.

Выборочные дисперсии каждого эксперимента статистически однородны, т.е. принадлежат одной и той же генеральной совокупности.        

Метод МНК можно применять в тех случаях когда выполняются все эти условия.

Результаты работы:

Таблица №7.