Лабораторная работа.
Получение статической модели по данным пассивного эксперимента.
Проверила
Выполнила
2004 г.
1 Оценка корреляционной матрицы
Матрица определяет связь одной входной величины с другой, если между ними зависимость. Зависимость коэффициентов определяется коэффициентами корреляции, чем меньше коэффициент корреляции, тем слабее связь. В данной лабораторной работе коэффициент корреляции равен 0,034 , следовательно, входные переменные являются независимыми. Этот факт позволяет использовать метод наименьших квадратов. В результате применения этого метода можно получить оптимальные оценки параметры выбранной структуры объекта и минимальную их дисперсию.
2 Оценка точности экспериментальных данных

Из полученных по заданию данных выделяются параллельные опыты, которые характеризуются одними и теме же значениями входных переменных.
|
N эксп. |
X1 |
X2 |
Y |
|
I |
1.181 1.110 |
1.393 1.288 |
17.272 16.925 |
|
II |
0.931 0.972 |
2.152 2.078 |
15.518 15.784 |
Для каждого эксперимента производиться вычисление двух показателей.
Выборочное математическое ожидания вычисляется по формуле:
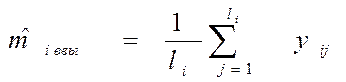 i=1,2,…,N
i=1,2,…,N
Точность или разброс относительно
среднего значения результата оценивается выборочной дисперсией, которая
рассчитывается по формуле:![]()
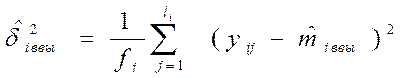 i=1,2,…,N
i=1,2,…,N
Для первого эксперимента:
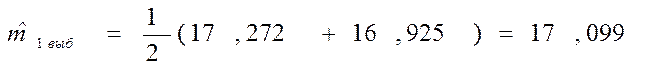
![]()
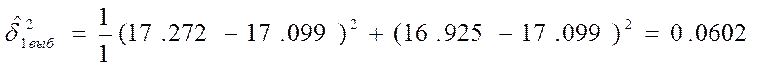 Для
второго эксперимента:
Для
второго эксперимента:
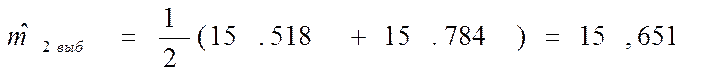
![]()
![]() Для
продолжения работы необходимо оценить однородность полученных выборочных
дисперсий, т.е. необходимо решить вопрос имеют ли полученные выборочные
дисперсии одно и то же генеральное значение.
Для
продолжения работы необходимо оценить однородность полученных выборочных
дисперсий, т.е. необходимо решить вопрос имеют ли полученные выборочные
дисперсии одно и то же генеральное значение.
Для этого производятся следующие действия:
1.Предполагаем, что все полученные измерения параметра X независимые случайные величины, они не связаны, взяты случайным образом из генеральной совокупности и имеющие нормальный закон распределения
2.Предполагаем, что полученные выборочные дисперсии являются однородными, а их различие вызвано случайными причинами. Формулируем гипотезы
![]() :
: ![]()
![]()
![]() :
: ![]()
![]()
3.Задаемся
вероятностью ошибки первого рода ![]()
4.Выбираем
статистику F-Фишера, двупараметрическую![]()
5.Находиться 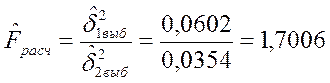
![]() и
и ![]()
6.По таблице
Фишера находиться ![]()
7.Принятие решения
![]()
Справедлива нулевая гипотеза с
вероятностью ![]() , это
значит что выборочные гипотезы однородны генеральной дисперсии, наши опытные
данные взяты из одной генеральной совокупности.
, это
значит что выборочные гипотезы однородны генеральной дисперсии, наши опытные
данные взяты из одной генеральной совокупности.
Далее находиться общая оценка данных в виде дисперсии воспроизводимости
![]()
![]()
![]()
![]()
![]()
3 Оценка значимости коэффициентов и адекватности модели
![]()
Оценка значимости коэффициентов модели
Для каждого коэффициента модели формулируется нулевая гипотеза в виде:
![]() :
: ![]()
и альтернативная гипотеза
![]() :
: ![]() ,
которая распадается на две
,
которая распадается на две ![]() и
и
![]()
Выбирается ![]() и
статистика Съюдента
и
статистика Съюдента
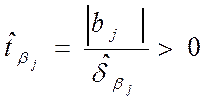
![]() , где
, где ![]()
![]() число
коэффициентов в рассчитанной модели
число
коэффициентов в рассчитанной модели
Найти критическую область
т.к. ![]() , то левая
часть всегда выполняется
, то левая
часть всегда выполняется
Поэтому нужно проверить
В этом случае справедлива нулевая
гипотеза с вероятностью ошибки ![]() .
.
Это означает, что данный коэффициент незначим, его генеральное математическое ожидание равно нулю и в уравнение он попал случайным образом. Его нужно убрать из уравнения, т.е. на самом деле его нет.
Если ,то справедлива альтернативная гипотеза, этот коэффициент значим, он должен присутствовать в уравнении принципиально, его отличие от нуля неслучайно.
Для данной модели ![]() и
и ![]()
Из всех коэффициентов модели значимым оказался только первый коэффициент
Адекватность модели
Сравнивается разброс опытных
данных относительно модели с точностью эксперимента. Точность оценивается по ![]() и
и ![]() , а также по
, а также по
![]() и
и ![]() , где
, где ![]() - число
параметров модели
- число
параметров модели
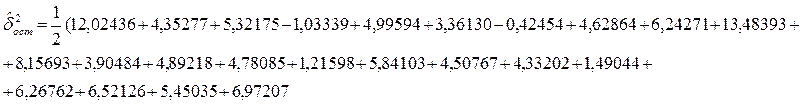
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.