Разработка системы управления. Математическое описание процесса получения зелёного щелока в растворителе плава, страница 2

(6)

Для вывода материального баланса абсолютно сухого вещества найдем производную по времени от количества абсолютно сухого вещества, находящегося в баке растворителя плава. Для некоторого момента времени она равна сумме расходов входящих и выходящих абсолютно сухих  веществ:

dGa/dt=G₄₂₂+G₄₁-G₄₃₂-G₄₄₂, где Ga-количество абсолютно сухих  веществ в баке растворителя плава при номинальном значении уровня зелёного щелока, кг;

G₄₂₂-расход а.с.в., поступающего в бак растворитель плава вместе со слабым белым щелоком, кг/с;

G₄₁- расход а.с.в., поступающего в бак растворитель плава вместе с плавом, кг/с;

G₄₃₂- расход а.с.в., откачиваемого из бака растворителя плава вместе с зелёным щелоком ,кг/с;

G₄₄₂- расход а.с.в., откачиваемого из бака растворителя плава вместе с пылегазовыми выбросами ,кг/с

(7)

Запишем уравнение (6) в абсолютных отклонениях:

d∆Ga/dt=∆G₄₂₂+∆G₄₁-∆G₄₃₂-∆G₄₄₂,

Абсолютные отклонения ∆Ga, ∆G₄₂₂, ∆G_41, ∆G₄₃₂, ∆G₄₄₂ могут быть определены из следующих  уравнении

Gа=V₁₂p₄₃₂

G₄₂₂= G₄₂k₄₂

G₄₃₂= G₄₃k₄₃

G₄₄₂= G₄₄k₄₄

где V₁₂-объём а.с.в.,в баке растворителе плава при номинальном значении уровня зелёного щелока,м³;

p₄₃₂-плотность а.с.в. в зелёном щелоке, кг/м³;

Тогда абсолютные отклонения параметров уравнения (8) будут равны:

∆Gа=∆V₁₂p₄₃₂

∆G₄₂₂= G_42\∆k₄₂+∆G₄₂k₄₂

∆G₄₃₂= G₄₃ ∆k₄₃+∆G₄₃k₄₃

∆G₄₄₂=G₄₄ ∆k₄₄+∆G₄₄k₄₄

(10)

Подставляя эти значения в уравнение (7), получим окончательное уравнение материального баланса а.с.в.:

p₄₃₂d∆V₁₂/dt= G_42\∆k₄₂+∆G₄₂k₄₂+∆G₄₁-G₄₃ ∆k₄₃-∆G₄₃k₄₃- G₄₄ ∆k₄₄-∆G₄₄k₄₄

В первом приближении можно считать, что:

Р₄₂=Р₄₂(k₄₂)

Р₄₃=Р₄₃(k₄₃,h)

Р₄₄=Р₄₄(k₄₄)

где Р₄₄ ,Р_43, Р₄₂ соответственно плотность слабого белого ,зелёного щелоков и пылегазовых выбросов ,кг/м³;

h-номинальное значение уровня зелёного щелока в баке растворителе плава, м.

Разложив эти функции в ряд Тейлора и пренебрегая членами второго и выше порядка ,получим:

∆р₄₂=( ¶р₄₂/¶к₄₂)∆к₄₂

(12)

∆ р₄₃=( ¶р₄₃/¶к₄₃)∆к₄₃+(¶р₄₃/¶h)∆h

∆р₄₄=( ¶р₄₄/¶к₄₄)∆к₄₄

отсюда имеем

(13)

∆ к₄₂=(¶ к₄₂/¶р₄₂)∆ р₄₂

∆ к₄₃=(¶ к₄₃/¶р₄₃)∆ р₄₃-(¶к₄₃/¶h)∆h

∆ к₄₄=(¶ к₄₄/¶р₄₄)∆ р₄₄

Сам процесс растворения плава в щелоке может быть описан следующими уравнениями состояния;

(14)

V₁₁+ V₁₂=V

P₄₃₁V₁₁+p₄₃₂V₁₂=р₄₃V

где V - рабочий объём щёлока в баке растворителе плава при номинальном значении уровня зелёного щёлока, м³.

Решая эту систему относительно V₁₁ и V₁₂ , получаем:

							(15)

 

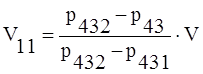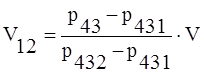Отсюда найдем абсолютные отклонения DV₁₁ и DV₁₂ :

						(16)

 

(17)

Рабочий объем щелока в баке растворителе плава равен:

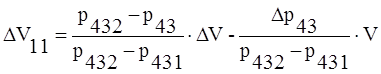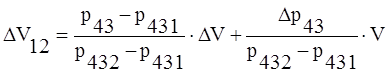V=F∙h

где F-поверхность зеркала испарения щелока в баке растворителя плава при номинальном значении уровня зеленого щелока, м³ .

(18)

Тогда абсолютные отклонения рабочего объема щелока DV в растворителе плава равны:

DV= F∙Dh

Подставляя значения абсолютных отклонений DV₁₁, DV₁₂, Dk₄₂, Dk₄₃, Dk₄₄ в уравнения (5) и (10), получим предварительную математическую модель управления параметрами зеленого щелока:

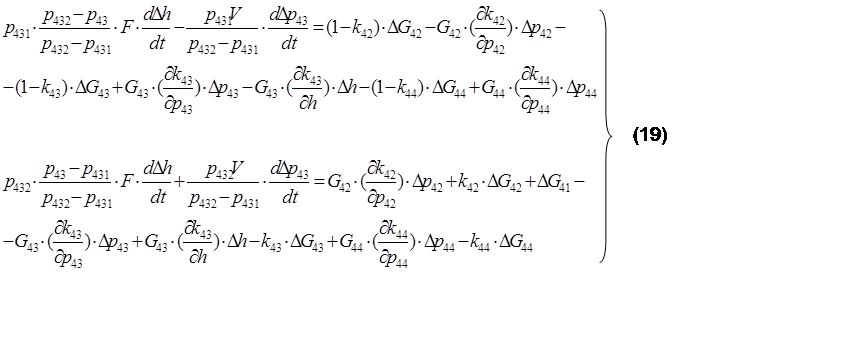
В свою очередь:

 

В первом приближении можно принять р₄₂₁=р₄₃₁=const, р₄₂₂=р₄₃₂=const, тогда значения частных производных могут быть определены по формулам:

 

В промышленных условиях обычно измеряют не массовые расходы щелоков, а объемные, т.е.:

 

Отсюда с учетом уравнений (20), (21) и (22), с одной стороны, и уравнения (19), с другой стороны, из совместного их решения составим окончательную математическую модель процесса получения зеленого щелока в канонической форме:

 

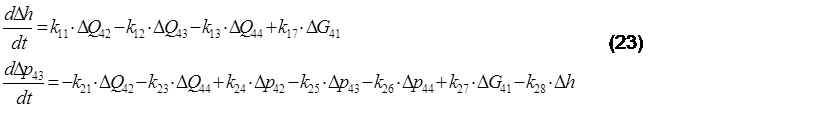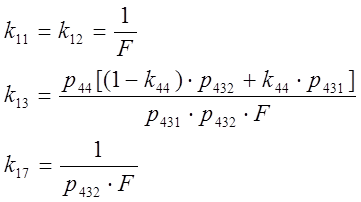где:

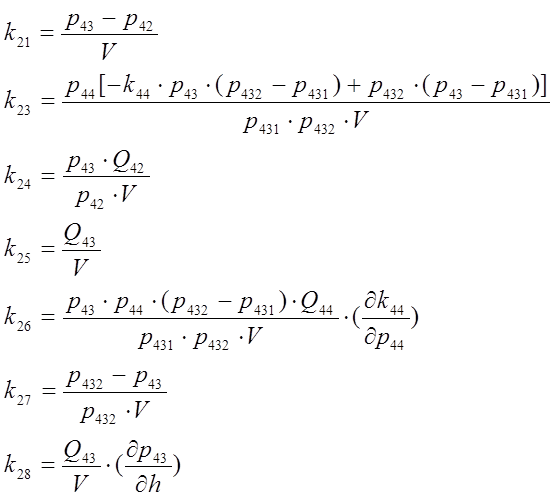
Разделив уравнения (23) на величину k₂₅и используя преобразования Лапласа, напишем окончательную математическую модель процесса получения зеленого щелока в операторной форме:

Dh(p)=W₁₁(p)DQ₄₂(p)- W₁₂(p)DQ₄₃(p)- W₁₃(p)DQ₄₄(p)+ W₁₇(p)DG₄₁(p)

(24)

Dp₄₃(p)=- W₂₁(p)DQ₄₂(p)- W₂₃(p)DQ₄₄(p)+ W₂₄(p)Dp₄₂(p)- W₂₆(p)Dp₄₄(p)+

+ W₂₇(p)DG₄₁(p)- W₂₈(p)Dh(p)

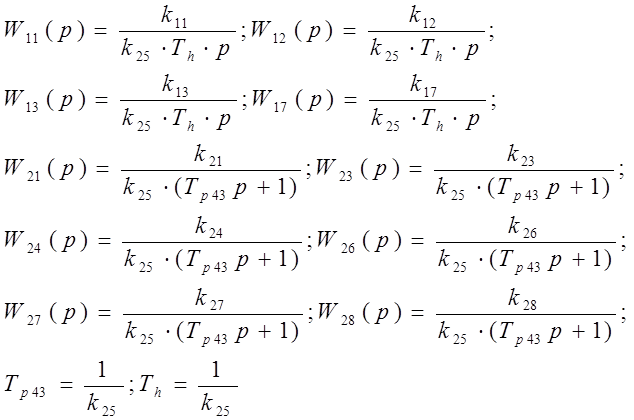где