Имитационное моделирование системы управления с учетом нелинейности «Зона нечувствительности с ограничениями»

САНКТ – ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

РАСТИТЕЛЬНЫХ ПОЛИМЕРОВ

Кафедра  АХТП

КУРСОВАЯ  РАБОТА

по дисциплине: «МОДЕЛИРОВАНИЕ СИСТЕМ»

на тему: «Имитационное моделирование системы управления с учетом нелинейности «Зона нечувствительности с ограничениями».

Выполнил:                                                                          студент группы 542

Проверил:                                                                                  

Санкт – Петербург

2004г.

1. Математическое описание исходных данных

1.1.  Элементы моделируемой системы

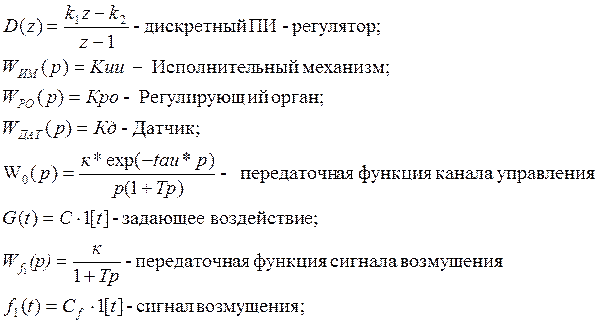
2. Нелинейный элемент

1.3.   Описание нелинейного элемента

В моделируемой системе в качестве нелинейного элемента используется регулирующий орган. Вид нелинейности – «зона нечувствительности с ограничениями»:

 

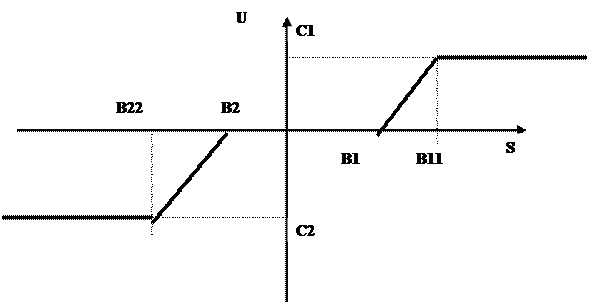Рис.2.Вид нелинейности .

C1,C2,B1,B2-параметры  нелинейности;     S-входной сигнал Р.О;     U-выходной сигнал Р.О.;

 

else

 

4. Входные сигналы

По каналу передачи управляющего воздействия:

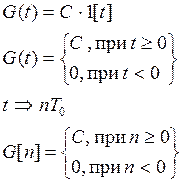
По каналу передачи возмущающего воздействия:

5.Определение дискретной модели непрерывной части системы и соответствующего разностного уравнения

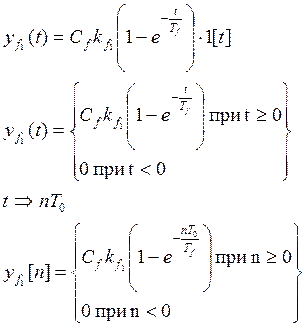
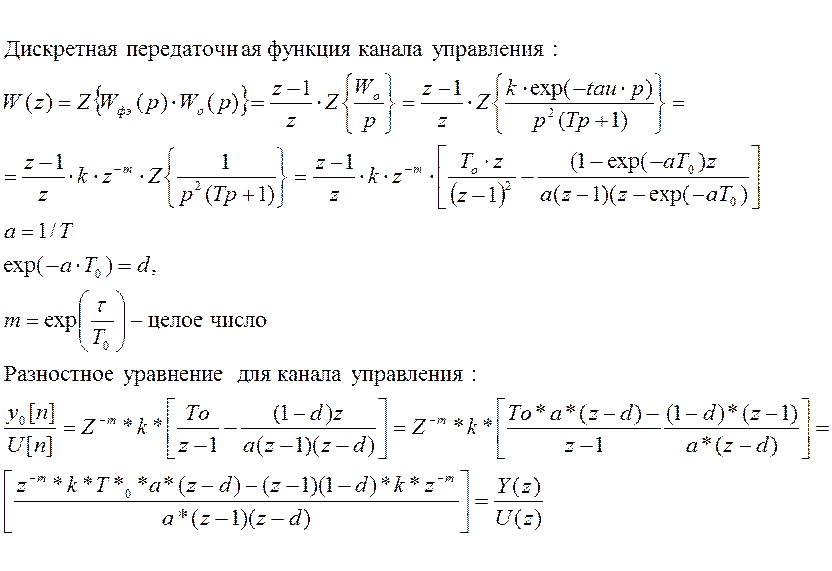
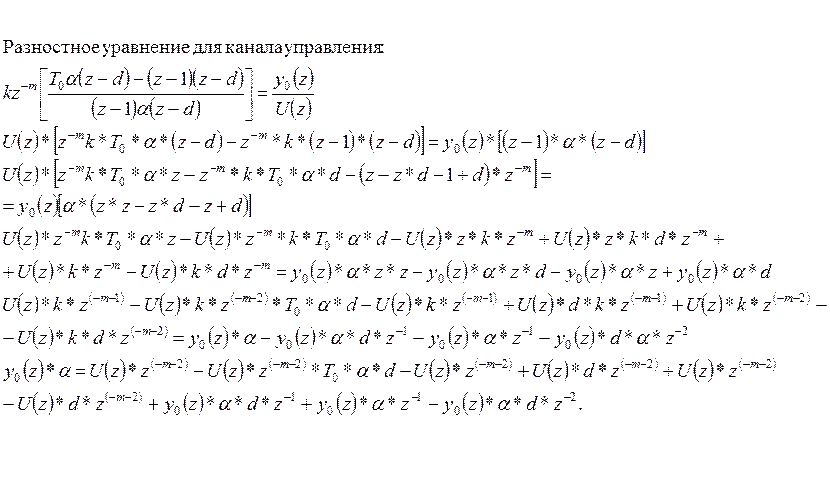
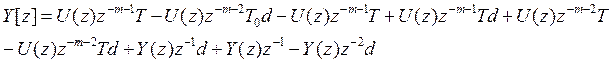
В итоге получили разностное уравнение в следующем виде:

Y[n]=U[n-m-1]*K*T - U[n-m-2]K*T_0*d – U[n-m-1]K*T +U[n-m-1]*K*d*T

+U[n-m-1]K*d*T+U[n-m-2]*K*T- U[n-m-2]K*d*T+ Y[n-1]*d+Y[n-1]-Y[n-2]*d.

6. Определение непрерывной и дискретной модели нелинейной характеристики

В системе имеет место нелинейность на выходе датчика. Входом нелинейного элемента является выход объекта y(t). Выходом – переменная нелинейного элемента y1(t).

5.Составление системы разностных уравнений, описывающих работу замкнутой системы управления. Анализ полученной системы уравнений для определения типа и первоначальных значений переменных

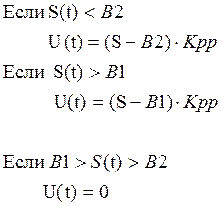
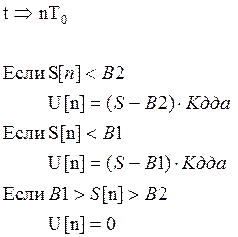
Для программирования данной системы необходимо перейти от дискретных функций элементов системы к разностным уравнениям.

Получим разностное уравнение для ПИ – регулятора:

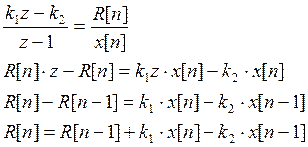
Объединив выведенные ранее разностные уравнения, можно получить систему разностных уравнений для описания работы одного такта расчета:

y0[n]:=U[n-m-1]*T*k-U[n-m-2]*T0*k*d-U[n-m-1]*T*k+U[n-m-1]*d*k*T +

U[n-m-2]*T*k-U[n-m-2]*d*k*T+y0[n-1]*d+y0[n-1]-y0[n-2]*d;

Yf1:=Cf1*Kf1*(1-exp(-I*T0/Tf1));

Y:=Y0[n]+Yf1;

Y1:=Kdat*Y;

X[n]:=Kdat*C0-Y1;

R:=R+X[n]*K1-X[n-1]*K2;

S:=Kim*R;

U[n]:=Kro*S;

if S<B22 then U[n]:=C2

else

if S>B11 then U[n]:=C1

else

if (S >B22) and (S <B2) then U[n]:=Kро*(S-B2)

else

if (S >B1) and (S <B11) then U[n]:=Kро*(S-B1)

else

U[n]:=0;

Для использования полученной системы в программе необходимо ввести массивы, простые переменные и переменные с первоначальным значением.

6. Эскизы форм  ввода, редактирования данных, вывода результатов моделирования в табличном и  графическом  виде.

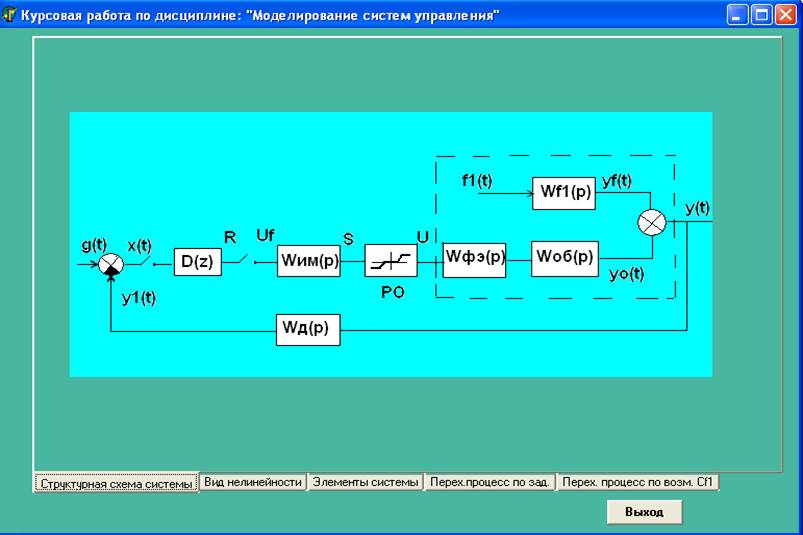
Рис.3. «Структурная схема системы»

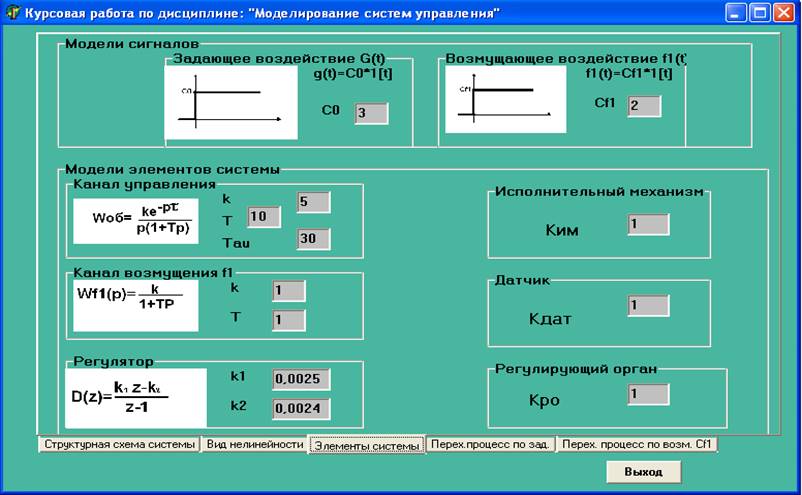
Рис.4. «Элементы системы»

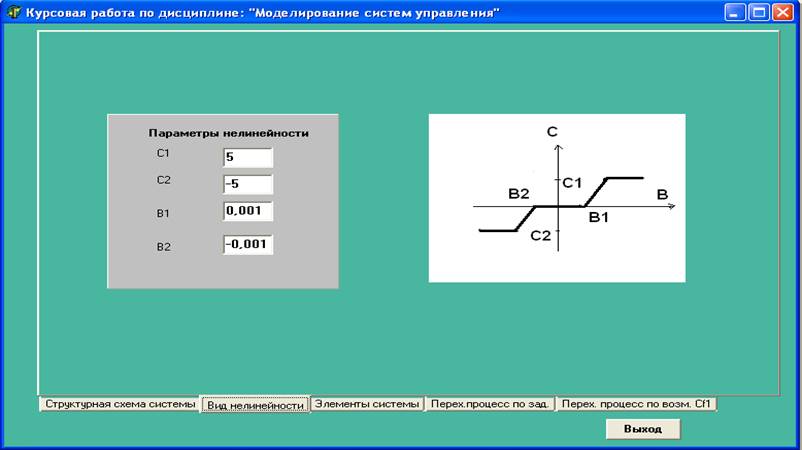
Рис.5. «Нелинейность»

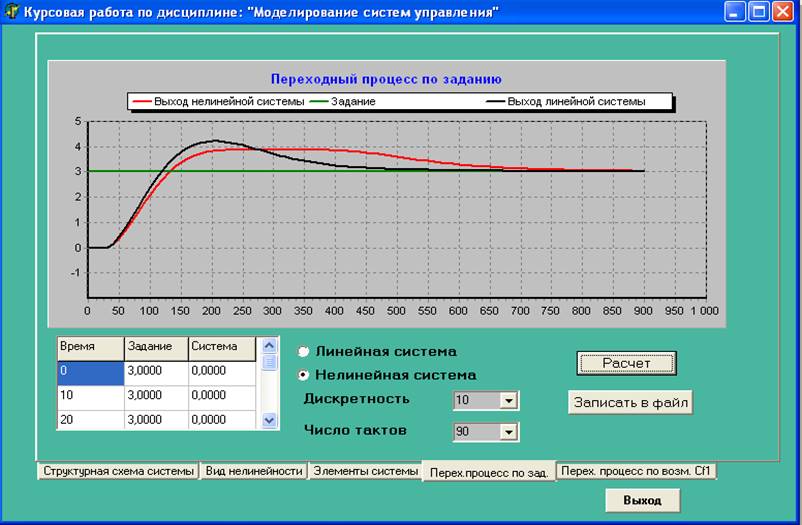
Рис.6. «Переходные процессы (по заданию)»

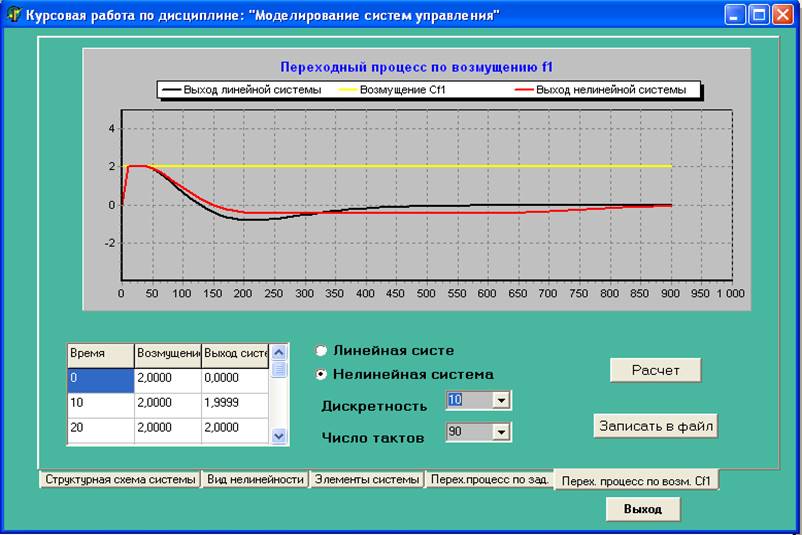
Рис.7. «Переходные процессы(по возмущению)»

7.Распечатка текста основного программного модуля/

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, ComCtrls, ExtCtrls, StdCtrls, TeeProcs, TeEngine, Chart, Grids,

Series;

type

TForm1 = class(TForm)

PageControl1: TPageControl;

TabSheet1: TTabSheet;

TabSheet2: TTabSheet;

TabSheet3: TTabSheet;

TabSheet4: TTabSheet;

TabSheet5: TTabSheet;

Button1: TButton;

Image1: TImage;

GroupBox1: TGroupBox;

GroupBox2: TGroupBox;

GroupBox3: TGroupBox;

Image2: TImage;

Image3: TImage;

Image5: TImage;

Panel1: TPanel;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Edit1: TEdit;

Edit2: TEdit;

Label4: TLabel;

Label5: TLabel;

Edit3: TEdit;

Edit4: TEdit;

Chart1: TChart;

Label6: TLabel;

Label7: TLabel;

ComboBox1: TComboBox;

ComboBox2: TComboBox;

RadioButton1: TRadioButton;

RadioButton2: TRadioButton;

Button2: TButton;

Button3: TButton;

StringGrid1: TStringGrid;

Chart2: TChart;

Label8: TLabel;

Label9: TLabel;

ComboBox3: TComboBox;

ComboBox4: TComboBox;

RadioButton3: TRadioButton;

RadioButton4: TRadioButton;

Button4: TButton;

Button5: TButton;

StringGrid2: TStringGrid;

Label10: TLabel;

Label11: TLabel;

Edit5: TEdit;

Label12: TLabel;

Label13: TLabel;

Edit6: TEdit;

GroupBox4: TGroupBox;

GroupBox5: TGroupBox;

GroupBox6: TGroupBox;

GroupBox7: TGroupBox;

GroupBox8: TGroupBox;

GroupBox9: TGroupBox;

GroupBox10: TGroupBox;

Image4: TImage;

Image6: TImage;

Image7: TImage;

Label14: TLabel;

Label15: TLabel;

Label16: TLabel;

Edit7: TEdit;

Edit8: TEdit;

Edit9: TEdit;

Label17: TLabel;

Label18: TLabel;

Edit10: TEdit;

Edit11: TEdit;

Label19: TLabel;

Label20: TLabel;

Edit12: TEdit;

Edit13: TEdit;

Label21: TLabel;

Edit14: TEdit;

Label22: TLabel;

Edit15: TEdit;

Edit16: TEdit;

Label23: TLabel;

Series1: TLineSeries;

OpenDialog1: TOpenDialog;

OpenDialog2: TOpenDialog;

Series2: TLineSeries;

Series3: TLineSeries;

Series4: TLineSeries;

Series5: TLineSeries;

Series6: TLineSeries;

procedure Button2Click(Sender: TObject);

procedure Button1Click(Sender: TObject);