
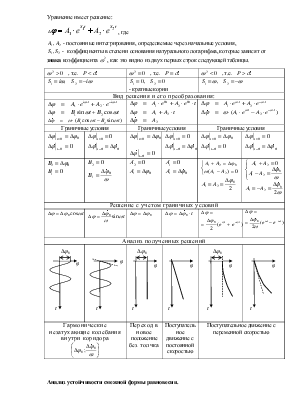


II семестр ЛЕКЦИЯ 3
Динамический критерий
В начале прошлой лекции дано следующее определение понятию устойчивость:
Равновесие называют устойчивым, если, задавшись любой величиной η>0, всегда можно указать
такую конечную величину ε>0, что при возмущении ψ< ε, характерное перемещение │Δ│< η.
В общем случае потеря устойчивости одного состояния равновесия системы и переход ее в новое равновесное состояние – это протекающий во времени процесс, полное описание которого требует динамического подхода.
Динамический подход подразумевает анализ свойств возмущенного движения, возникающего после нарушения исследуемого состояния равновесия. Если при этом система остается в окрестности состояния равновесия, то это состояние считается устойчивым.
Оценим устойчивость двух форм равновесия – первоначальной и смежной – системы, для которой ранее использовался статический подход (метод Эйлера, энергетический критерий).
Предположим некоторое малое возмущение равновесного состояния в начальный момент времени. Далее система может находиться в состоянии свободных колебаний или иного движения, осуществляемого без доступа энергии извне.
*)Напоминание: уравнение
движения массы ![]() , обладающей одной степенью
свободы q, при
отсутствии вынуждающей силы
, обладающей одной степенью
свободы q, при
отсутствии вынуждающей силы
![]() или
или
![]() .
.
Пусть ![]() –угол поворота,
характеризующийотклонение от равновесного состояния в произвольный
момент времени, т.е. степень свободы. В таком случае инерционный коэффициент
представляет собой момент инерции массы
–угол поворота,
характеризующийотклонение от равновесного состояния в произвольный
момент времени, т.е. степень свободы. В таком случае инерционный коэффициент
представляет собой момент инерции массы ![]() .
.
Анализ устойчивости первоначальной формы равновесия.
Уравнение движения (без учета диссипативных сил:
![]() ;
;
![]() ;
;
![]() , где
, где 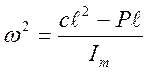 .
.
Уравнение имеет решение:
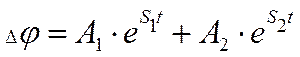 , где
, где
![]() - постоянные
интегрирования, определяемые через начальные условия,
- постоянные
интегрирования, определяемые через начальные условия,
![]() -
коэффициенты в степени основания натурального логарифма, которые зависят от знака
коэффициента
-
коэффициенты в степени основания натурального логарифма, которые зависят от знака
коэффициента ![]() , как это видно из двух первых строк
следующей таблицы.
, как это видно из двух первых строк
следующей таблицы.
|
|
|
|
||||||
|
|
- кратные корни |
|
||||||
|
Вид решения и его преобразования: |
||||||||
|
|
|
|
||||||
|
Граничные условия |
Граничные условия |
Граничные условия |
||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
Решение с учетом граничных условий |
||||||||
|
|
|
|
|
|
|
|||
|
Анализ полученных решений |
||||||||
|
|
|
|
|
|
|
|||
|
Гармонические незатухающие колебания внутри
коридора |
Переход в новое положение без толчка |
Поступательное движение с постоянной скоростью |
Поступательное движение с переменной скоростью |
|||||
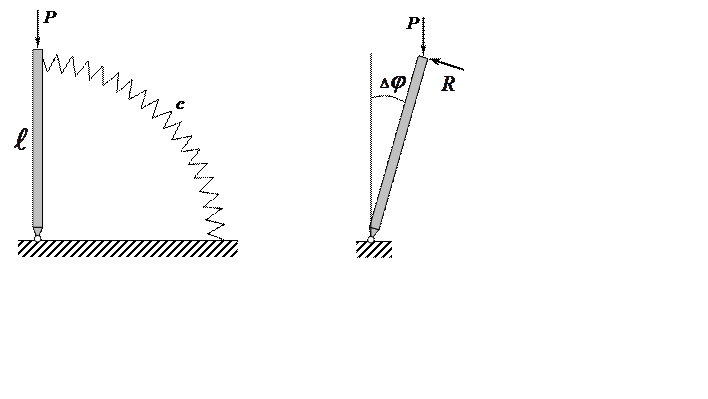
Анализ устойчивости смежной формы равновесия.
Это положение равновесия возможно только при  .
.
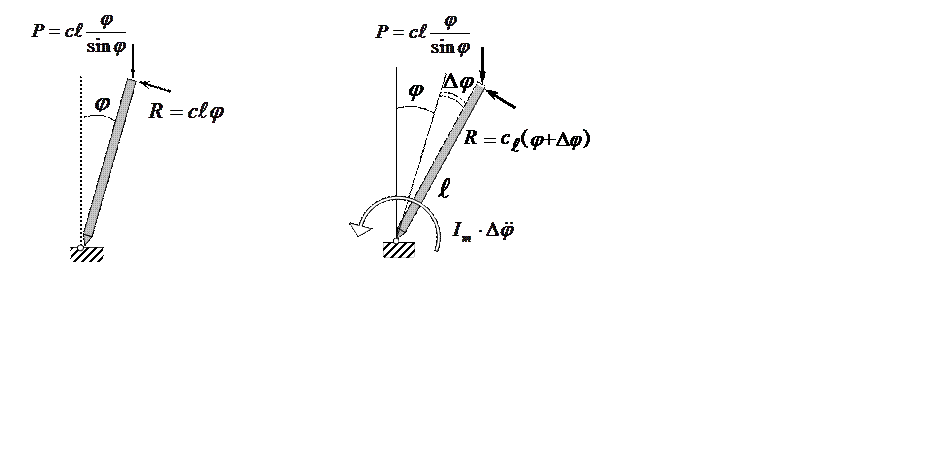
Обратим внимание на то, что:
Момент сил инерции определяется отклонением от положения равновесия Δj.
Тогда уравнение движения имеет вид:
![]() .
.
Приведем его к виду ![]() :
:

![]() ;
;
В предположении малости угла Δj
![]() .
.
После подстановки полученного выражения в уравнение движения получаем:
![]() и, таким образом
и, таким образом
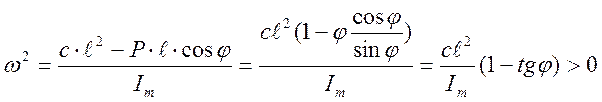 .
.
Рисунок поясняет утверждение о том, что коэффициент ![]() в дифференциальном уравнении
положителен, и, как следует из проведенного выше исследования решения
(таблица), положение равновесия устойчиво.
в дифференциальном уравнении
положителен, и, как следует из проведенного выше исследования решения
(таблица), положение равновесия устойчиво.
Тема 2.
Устойчивость
прямолинейного сжато-изогнутого стержня (![]() и
и
![]() )
)
2.1 Уравнение равновесия сжато-изогнутого стержня
Рассматривается устойчивость «в смысле Эйлера»; этоозначает, что приняты следующие допущения:
Длина, площадь сечения и момент инерции в процессе нагружения остаются неизменными.
Изгиб стержня при потере устойчивости описывается обычной теорией изгиба балок.
форма равновесия, приобретенная после потери устойчивости прямолинейной формы, смежна с первоначальной формой (перемещения малы).
Благодаря первому предположению, при отсутствии
поперечной нагрузки (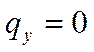 )
первоначальная прямолинейная форма может быть равновесной. Эта ситуация
описывается приведенными ниже соотношениями:
)
первоначальная прямолинейная форма может быть равновесной. Эта ситуация
описывается приведенными ниже соотношениями:

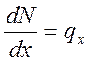 ,
, 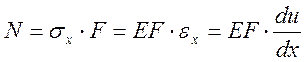 ;
;
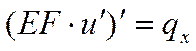 –
–
– дифференциальное уравнение
второго порядка. Решение ![]() содержит две
постоянные интегрирования, для определения которых формулируются два граничных
условия относительно перемещения u,
после чего задачу можно считать решенной. Соответствующую прямолинейной форме
функцию
содержит две
постоянные интегрирования, для определения которых формулируются два граничных
условия относительно перемещения u,
после чего задачу можно считать решенной. Соответствующую прямолинейной форме
функцию ![]() обозначим
обозначим ![]() .
.
Благодаря второму предположению при потере устойчивости изгиб стержня можно описывать обычной теорией изгиба балок:
![]()
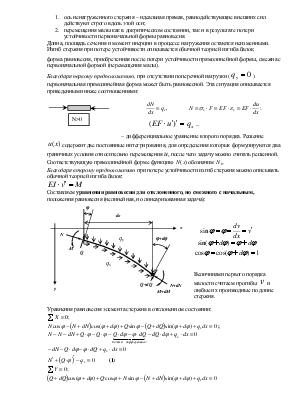
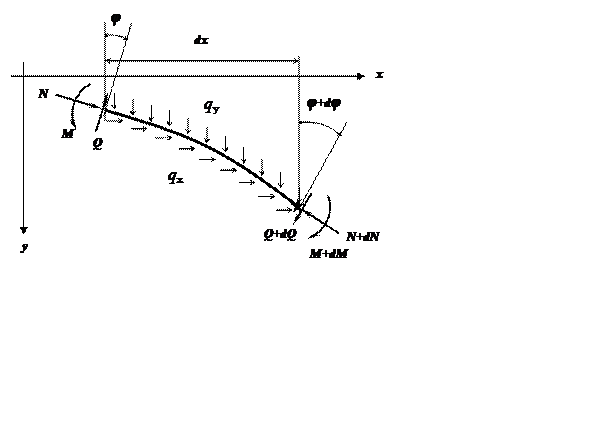 Составляем уравнения равновесия для отклоненного, но смежного с
начальным, положения равновесия (нелинейная, но линеаризованная задача):
Составляем уравнения равновесия для отклоненного, но смежного с
начальным, положения равновесия (нелинейная, но линеаризованная задача):
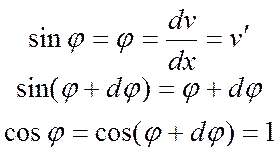
Величинами первого порядка малости считаем прогибы ![]() и любые их производные по длине
стержня.
и любые их производные по длине
стержня.
Уравнения равновесия элемента стержня в отклоненном состоянии:
![]()
![]() ;
;
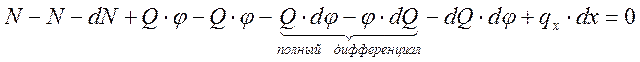
![]()
![]() (1)
(1)
![]()
![]()
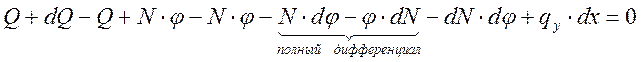
![]() (2)
(2)
![]()
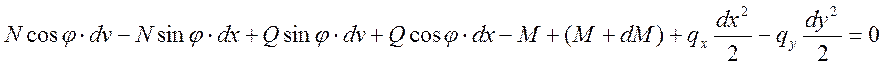
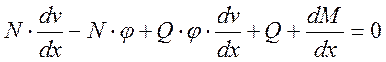
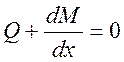 (3)
(3)
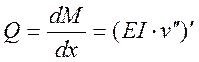 - бесконечно
малая величина. Следовательно, второе слагаемое в формуле (1) – также бесконечно
малая величина высшего порядка малости и уравнение (1) принимает знакомый
вид
- бесконечно
малая величина. Следовательно, второе слагаемое в формуле (1) – также бесконечно
малая величина высшего порядка малости и уравнение (1) принимает знакомый
вид 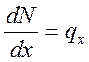 .
.
Кроме того, при малых отклонениях изменения граничных условий относительно продольных перемещений также имеют 2 порядок малости.
Таким образом, на основании уравнений (1) и (3) можно сделать вывод, что при бифуркационных отклонениях продольная сила получает изменение на величину высшего порядка малости, иными словами, совпадает с продольной силой первоначальной формы равновесия.
Дальнейшее преобразование формулы (2) приводит к виду:
![]() .
.
В случае призматического стержня (EI=const), нагруженного по торцам (N=const)
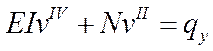 .
.
В случае центрального сжатия:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.