|
Министерство образования Республики Беларусь Гомельский государственный технический университет им. П.О. Сухого Кафедра ТОЭ Расчетно-пояснительная записка к заданию №1: Расчет линейных цепей трехфазного синусоидального тока. Выполнил студент гр. ЭП-21
Принял преподаватель
Гомель 2005 |
Расчет линейных цепей трехфазного синусоидального тока.
Вариант задания: 348
Схема электрической цепи.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


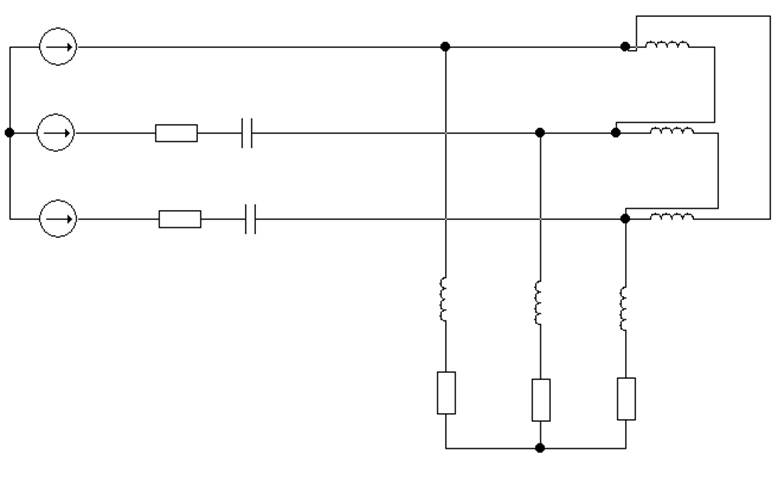
Рис.1
Таблица численных значений параметров схемы.
|
UА |
R1 |
R2 |
XC1 |
XL2 |
XL3 |
|
B |
Ом |
Ом |
Ом |
Ом |
Ом |
|
400 |
6 |
4 |
2 |
8 |
6 |
К симметричному трехфазному генератору через сопротивления линии передачи подключены два трехфазных приемника электрической энергии. Вследствие аварии произошло замыкание накоротко одного из сопротивлений или разрыв цепи.
Программа работы:
Ø Найти все токи и напряжения в нагрузке и на линии.
Ø Определить показания ваттметров.
Ø С помощью балансов активных и реактивных мощностей проверить результаты расчетов токов, напряжений и показаний ваттметров.
Ø Построить векторную лучевую и векторную топографическую диаграммы токов и напряжений.
2.Расчет напряжений и токов в нагрузке и на линии.
Исходные данные:
![]()
Так как сопротивления линейных проводов и фаз приёмников в комплексной форме записи равны
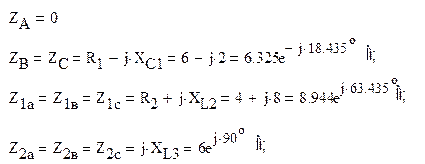
то исходная электрическая схема может быть представлена в виде (Рис.2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
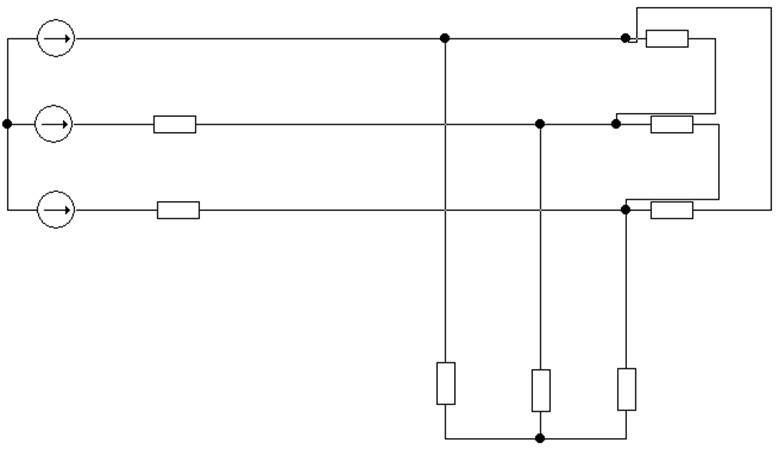
Рис.2
2.1 Преобразование исходной электрической схемы.
Сопротивления фаз Z1a, Z1в, Z1c симметричного приемника, соединенного звездой, можно заменить эквивалентным треугольником (Рис.3), сопротивления Z1ав, Z1вc, Z1ca которого равны:
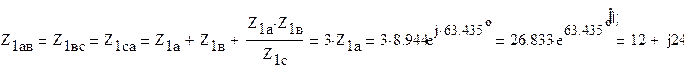
Так как Z1aв параллельно Z2в, а Z1вc - Z2с и Z1ca - Z2а, то
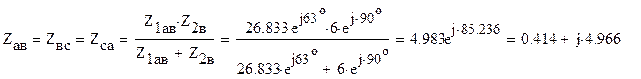
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
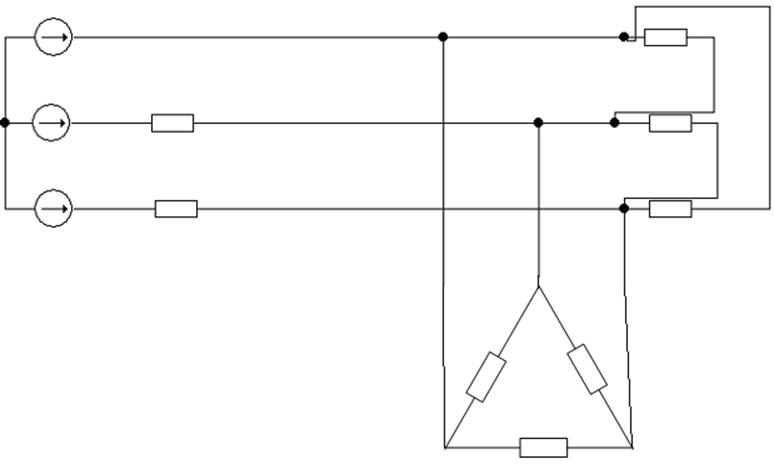
Рис.3
и новый эквивалентный треугольник будет иметь вид, представленный на рисунке 4.
![]()
![]()
![]()
![]()
![]()
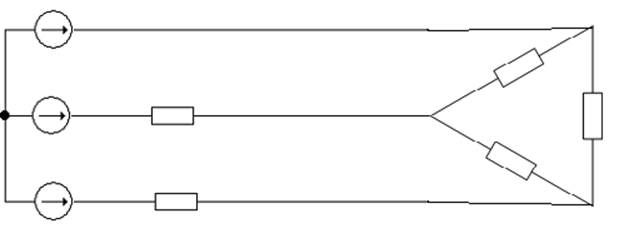
Рис.4
Треугольник сопротивлений Zав, Zвс, Zca, в свою очередь, можно преобразовать в эквивалентную звезду (Рис.5), сопротивления которой
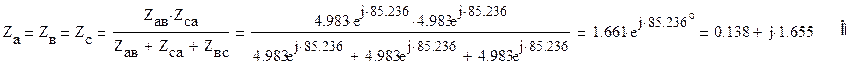
![]()
![]()
![]()
![]()
![]()
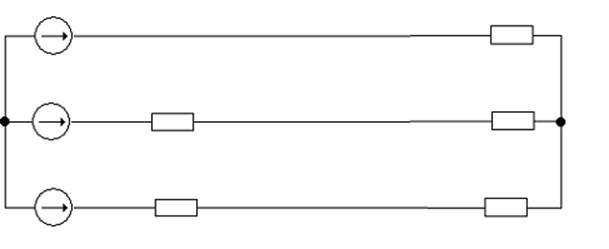
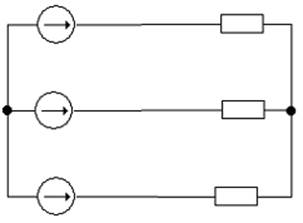
Рис.5
Наконец, сопротивления ZB и Za, ZC и Zc соединены последовательно, что позволяет заменить их соответствующими эквивалентными сопротивлениями (Рис.6)
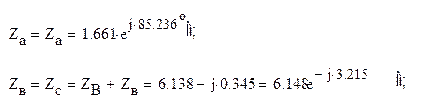
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.2 Определение напряжения смещения нейтрали.
При определении напряжения UnN воспользуемся методом двух узлов, согласно которому
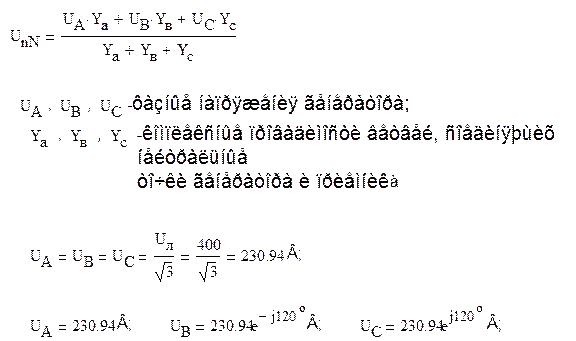
В свою очередь, комплексные проводимости
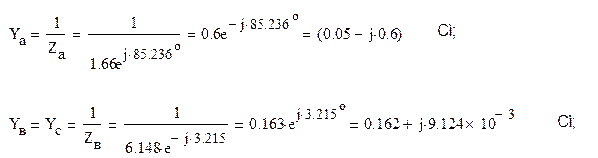
Тогда напряжение смещения нейтрали
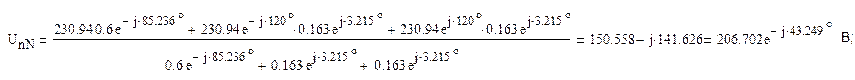
2.3 Определение реальных токов и напряжений
Так как напряжения на фазах эквивалентного приемника (Рис.6) равны
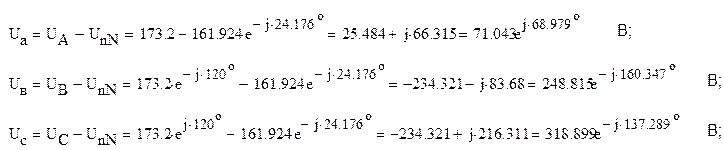
то линейные токи IA, IB и IC можно определить по закону Ома:
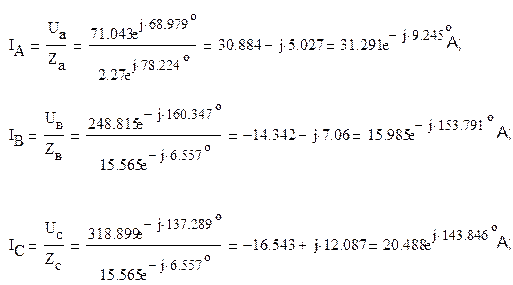
![]()
Зная токи IA, IB и IC, легко найти падения напряжений на сопротивлениях линии.
По закону Ома
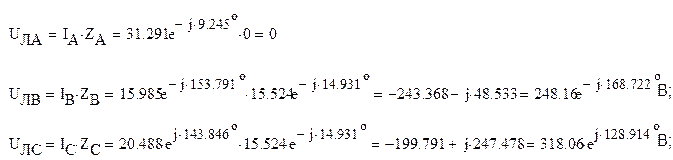
Далее, используя второй закон Кирхгофа, можно определить напряжения:
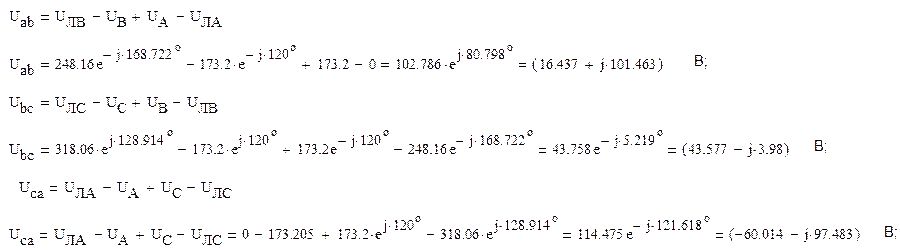
Наконец, токи в фазах приемников определяются так:
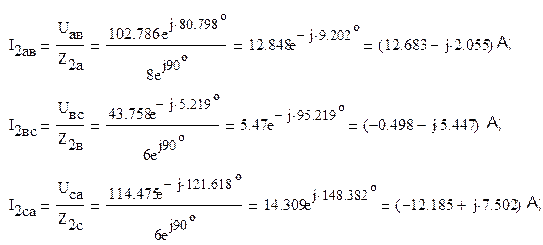
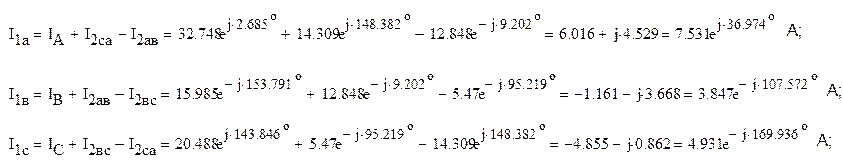
3.Расчет показаний ваттметров.
В схеме трехфазной цепи ваттметры включены так, что к одному из них подводятся напряжения Uaс и ток IA, а ко второму – напряжение Uвc и ток IВ. Следовательно, показания ваттметров будут равны:
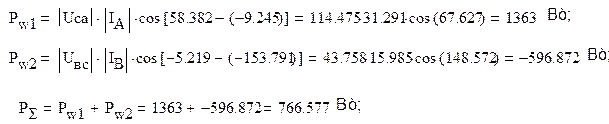
1. Баланс активных и реактивных мощностей.
Полная комплексная мощность трехфазного источника
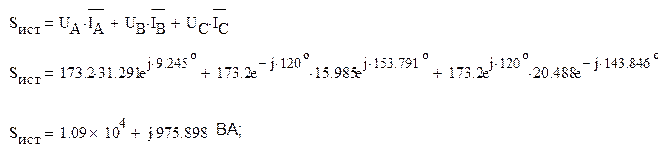
Значит, активная и реактивная мощности источника
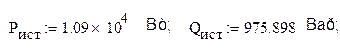
Активная мощность, потребляемая приемником
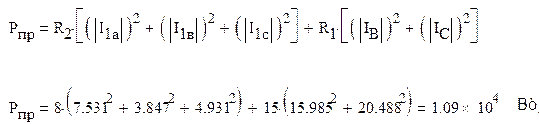
и реактивная мощность
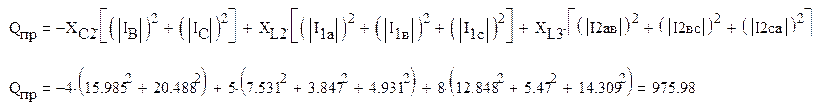
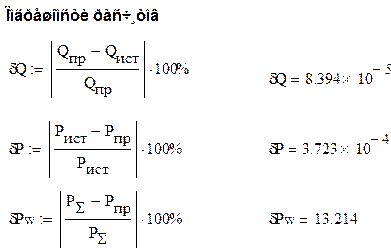
5. Построение векторных диаграмм токов и напряжений.
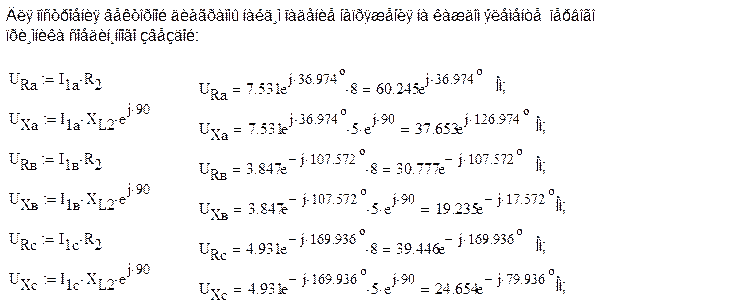
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.