Задача №2
ТЕМА: Расчёт линейной электрической цепи постоянного тока с несколькими источниками электрической энергии
Для
цепи изображённой на рисунке 2.1 известны ЭДС с внутренним сопротивлениями ![]() и
и ![]() источников питания, а также
сопротивления
источников питания, а также
сопротивления ![]() .
.
Необходимо:
1. Составить систему уравнений для расчёта электрической цепи методом уравнений Кирхгофа
2. Определить токи в ветвях методом контурных токов
3. Определить токи в ветвях методом узловых потенциалов
4. Определить ток ветви, в которой отсутствуют источники ЭДС методом эквивалентного генератора.
5. Составить уравнение баланса мощности
6. Построить потенциальную диаграмму для конура, в котором два источника ЭДС
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
1 |
75 |
0.2 |
15 |
0.8 |
4 |
3 |
7 |
6 |
6 |
6 |
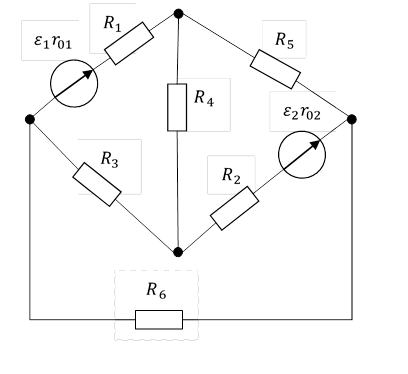
Рисунок 2.1 схема цепи
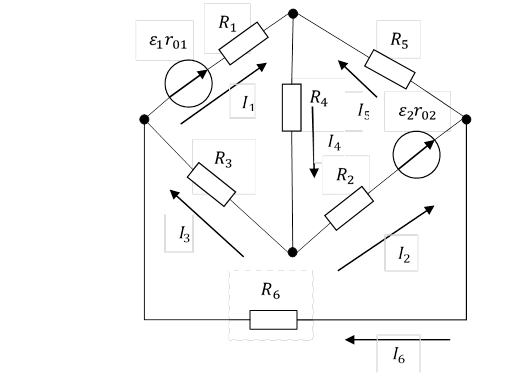
Рис 2.2
Система уравнений для определения токов путём непосредственного применения законов Кирхгофа для данной цепи изображённой на рисунке 2,2 будет иметь вид:
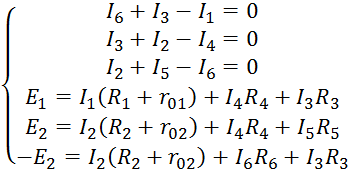
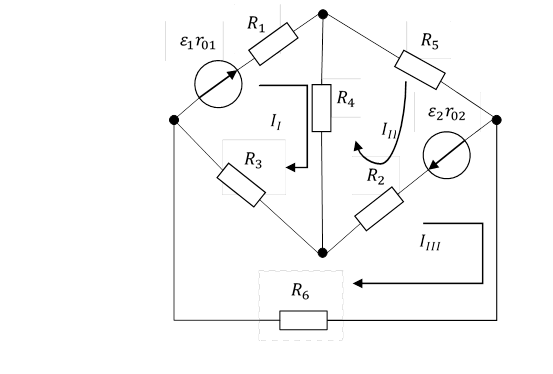
Рис2.3 схема цепи с изображёнными направлениями обхода контуров
Составляем уравнения по второму закону Кирхгофа:
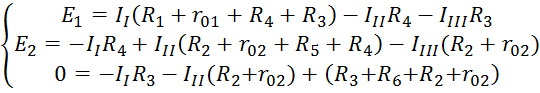
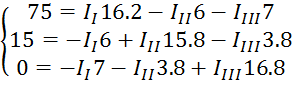
Составим определители:
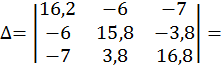
![]()
![]()
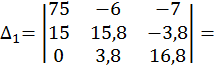
![]()
![]()
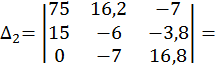
![]()
![]()
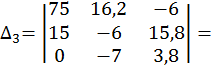
![]()
![]()
Определим токи контуров:
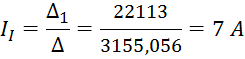
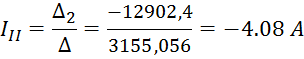
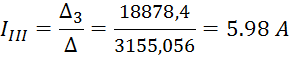
Второй
ток получился с минусом, следовательно, ток ![]() направлен в другую сторону.
Рассчитаем токи цепи с учётом перенаправления тока
направлен в другую сторону.
Рассчитаем токи цепи с учётом перенаправления тока![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Правильность решения проверим составлением баланса мощности:
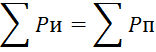
![]()
![]()
![]()
![]()
Баланс составлен правильно, но с небольшой погрешностью. Рассчитаем погрешность:
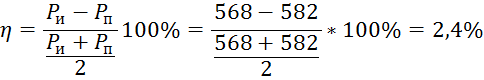
Методом узловых потенциалов. Заземлим узел №4 то есть сделаем его потенциал равным 0:
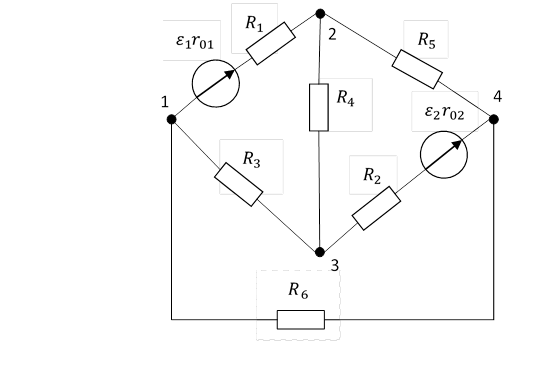
Рис 2.4
Определим проводимости узлов и ветвей электрической цепи:
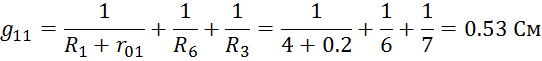
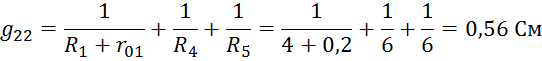
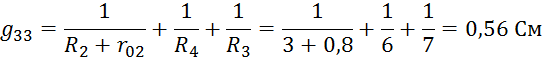
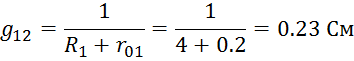
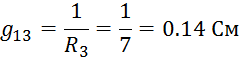
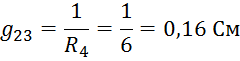
Составим систему уравнений:
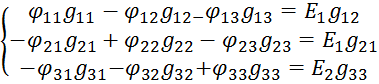
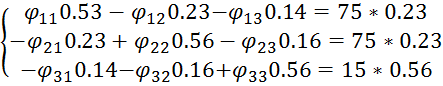
Составим определители:
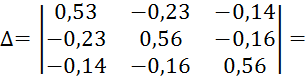
![]()
![]()
![]()
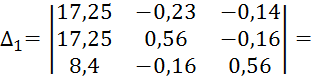
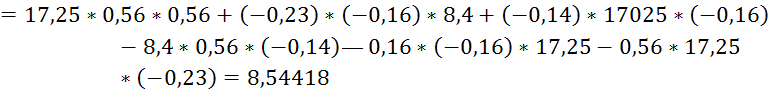
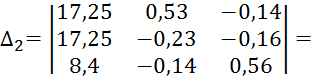
![]()
![]()
![]()
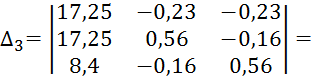
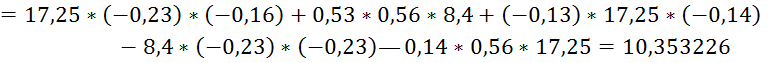
Определим потенциалы точек:
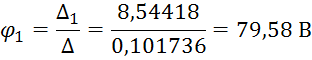
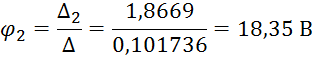
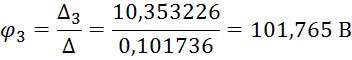
Найдём токи ветвей:
![]()
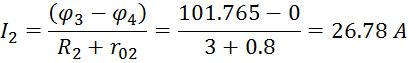
![]()
![]()
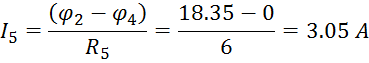
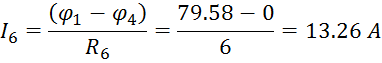
Правильность решения проверим составлением баланса мощности:
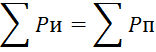
![]()
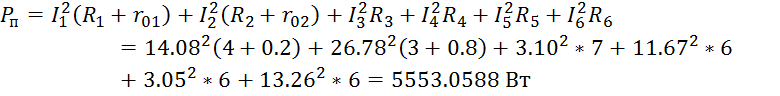
Баланс мощности составлен не правильно возможно в решении были допущены ошибки.
Отключим резистор ветви, в которой отсутствуют ЭДС, а именноR6:
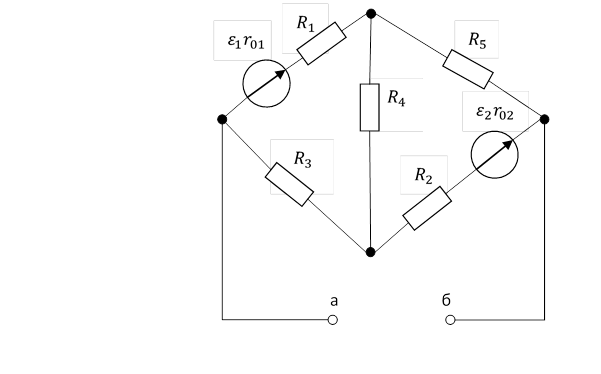
Рис2.5
Определим ток холостого хода эквивалентного генератора:
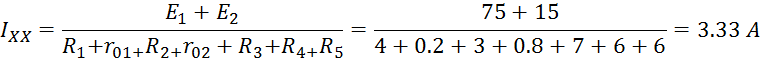
Пусть точка «а» заземлена тогда будет верно выражение:
![]()
Найдём напряжение холостого хода:
![]()
Для
определения внутреннего сопротивления эквивалентного генератора требуется
эквивалентный треугольник сопротивлений ![]() заменим эквивалентной звездой
сопротивлений
заменим эквивалентной звездой
сопротивлений ![]() :
:
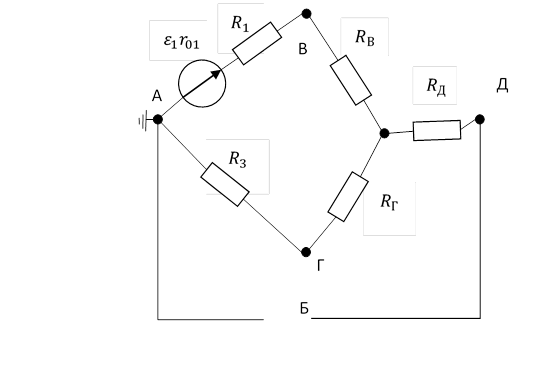
Рис 2,6
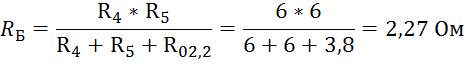
Так
как ![]() то и сопротивления
то и сопротивления ![]()
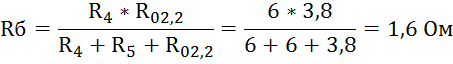
Найдём эквивалентное сопротивление генератора:
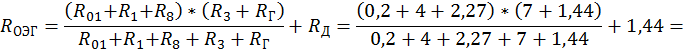
![]()
Определим
ток ![]() :
:
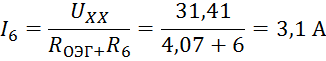
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.