При использовании апериодических регуляторов значение такта квантования однозначно определяет длительность процесса регулирования. Для регулятора АР длительность процесса регулирования составит m- тактов, здесь m порядок дискретной передаточной функции объекта. Для регулятора АР+1 длительность процесса регулирования составит m+1- тактов. Таким образом, чем меньше такт квантования, тем меньше длительность процесса регулирования. Но, с другой стороны, с уменьшением такта квантования увеличиваются отклонения управляющей переменной и затраты на регулирование. Поэтому принято выбирать значения такта квантования по следующим соотношениям:
T0/TΣ ³ 0.36 T0/T95 ³ 0.18
где TΣ - сумма постоянных времени объекта;
T95 - время достижения выходной величины значения 0,95 от установившегося значения на переходной характеристике.
Таким образом, основной такт квантования выбираем по указанным соотношениям, а промежуточный такт выбираем кратным основному в 2¸8 раз меньше.
Можно получить дискретную передаточную функцию объекта из дифференциального уравнения, описывающего динамику объекта. Затем по этому уравнению составить разностное уравнение, по которому с использованием теоремы о сдвиге вправо построить дискретную передаточную функцию объекта.
Привычнее описание динамики объекта непрерывными передаточными функциями, использующими преобразование Лапласа. Поэтому используем переход от непрерывной передаточной функции к дискретной.
В дискретных системах управления непрерывное звено обычно имеет на входе экстраполятор нулевого порядка
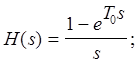
С учетом эктраполятора дискретную передаточную функцию отыскивают по выражению:
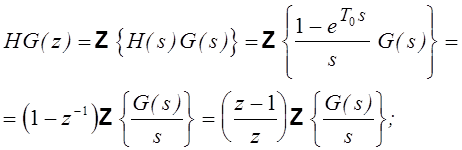
Например, имея непрерывную передаточную функцию апериодического звена
ищем дискретное преобразование для выражения
и, домножая на выражение в скобках, учитывающее экстраполятор, получаем дискретную передаточную функцию непрерывного звена с экстраполятором на входе
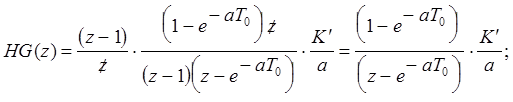
После приведения к нормальному виду получаем
где 
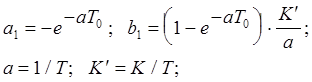
Например, если апериодическое звено имеет коэффициент передачи K=1, постоянную времени T=7.5c, то при такте квантования T0 =4c его дискретная передаточная функция имеет следующие параметры:
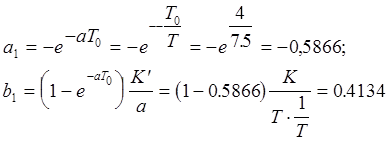
В общем случае нормальный вид дискретной передаточной функции объекта регулирования
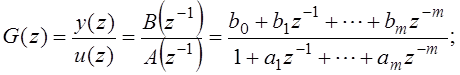
из которой получаем уравнение
и используя теорему о сдвиге получаем разностное уравнение
, а из него рекуррентную формулу для расчета
переходного процесса изменения выходной величины y(k)
Например, можно определить реакцию апериодического звена на управляющее воздействие следующей формы:
u(-0)=0; u(+0)=2; u(1)=1.5; u(2)=1.0; u(k)=1.0 при k=3,4,5. . . .
при такте квантования T0 =4c
По разностному уравнению
определяем значения выходной величины для k-х моментов времени
y(0) = 0.5866*0 + 0.4134*0 = 0
y(1) = 0.5866*0 + 0.4134*2 = 0.8268
y(2) = 0.5866*0.8268 + 0.4134*1.5 = 1.1051
y(3) = 0.5866*1.1051 + 0.4134*1.0 = 1.0617
y(4) = 0.5866*1.0617 + 0.4134*1.0 = 1.0362
y(5) = 0.5866*1.0362 + 0.4134*1.0 = 1.0212
y(6) = 0.5866*1.0212 + 0.4134*1.0 = 1.0125
y(7) = 0.5866*1.0125 + 0.4134*1.0 = 1.0073
Переходную характеристику объекта получают рассчитывая переходный процесс изменения выходной переменной объекта y(k)при единичном скачке управляющей переменной u(k) на входе
Для построения переходной характеристики задают управляющее воздействие следующей формы:
u(k) = 1 при k = 0,1, 2, . . .
и рассчитывая выходную переменную по следующей формуле
по результатам расчета строят таблицу и график переходной характеристики объекта y(k).
Дискретный апериодический регулятор АРимеет передаточную функцию, синтезируемую по параметрам передаточной функции объекта, когда задан вид переходного процесса на выходе САР. По этому условию переходный процесс заканчивается через m-интервалов, а выход САР достигает заданного значения.
В зависимости от параметров объекта передаточная функция апериодического регулятора вычисляется следующим образом
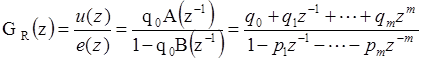
здесь A(z-1) и B(z-1) - полиномы из передаточной функции объекта регулирования
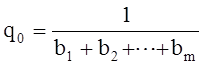
q1 = q0a1 p1= q0b1
q2 = q0a2 p2= q0b2
¼¼¼¼ …………
qm = q0am pm= q0bm
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.