Алгебраические критерии устойчивости. Критерий Гурвица. Устойчивость системы автоматического регулирования

ВОПРОС 9.       АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ

В ТАУ разработаны способы исследования устойчивости САУ, которые позволяют судить об устойчивости без нахождения корней характеристического уравнения. Способы делят на: 1) алгебраический способ; 2) частотный способ.

В ТАУ их принято называть критериями. В алгебраических критериях устойчивость определяется коэффициентом характеристического уравнения, в частотных критериях – по частотным характеристикам, либо по искусственно придуманным, либо по частотной характеристике всей системы, т.е. АЧХ и ФЧХ. Системы замкнутые.

Критерий Гурвица.  Удобно использовать для исследования систем невысокого (до 6-го) порядка. Для исследования:

1. Составляется таблица Гурвица из коэффициентов характеристического уравнения а₀рⁿ + а₁р^n-1 + а₂р^n-2 +…+ а_n-2р² + а_n-1р + а_n = 0

Таблица содержит n-строк и n-столбцов, где n – порядок характеристического уравнения. 1-ая строка составляется из коэффициентов характеристического уравнения с нечетными индексами, 2-ая строка с четными индексами, начиная с а₀. Так как столбцов n, а коэффициентов с нечетными и четными индексами в 2 раза меньше, то коэффициентами заполнится половина строки, остальные места заполняются 0; 3-ая – формируется из 1-ой сдвигом 1-ой строки вправо на 1 элемент, освободившееся место заполняется 0; 4-ая строка формируется аналогично из 2-ой и т.д., чтобы главная диагональ матрицы выглядела: а₁, а₂, а₃, …, а_n.

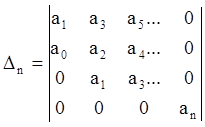
Устойчивость системы автоматического регулирования определяется условием, что определитель  и его диагональные миноры

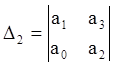
и т. д. положительны.

Определение с помощью критерия Гурвица достаточных условий устойчивости систем 1-2 порядков

1)           а₀р + а₁ = 0;         ;             а1 > 0 (т.к. условие устойчивости

2)           а₀р² + а₁р +а₂ = 0;                            n = 2

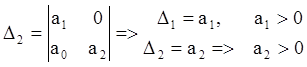            условие устойчивости

исследование устойчивости заключается в том, что определяют не только устойчива система или нет, но и в оценке какие параметры и как влияют на устойчивость.

Существует второй способ – алгебраический критерий Рауса, который применим для исследования систем высокого порядка.

Критерий Рауса применяется для исследования систем высокого порядка, когда n = 3. Для исследования составляется таблица Рауса из (n+1) строк и 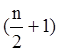 столбцов для четных n,  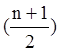столбцов для нечетных n.

Критерий:           Система устойчива, если коэффициенты 1-го столбца таблицы положительны. Каждое изменение знака коэффициентов 1-го столбца соответствует одному корню с положительной вещественной частью.

Коэффициенты Рауса

Элемент с_ki таблицы Рауса можно вычислить:

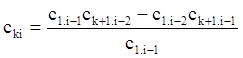
По критерию Рауса каждому изменению знака коэффициентов 1-го столбца соответствует один положительный корень (т.е. а₁ > 0, c₃₁ > 0, c₄₁ > 0,…, c_n1.1 > 0) .