Другие предметы \ Теоретическая метрология

Однократное измерение. Измерение параметров процессов и полей. Многократное измерение одной и той же физической величины постоянного размера, страница 5

Qi

80

83

84

85

86

87

88

89

90

91

92

m

1

1

1

3

3

3

4

2

4

1

1

 4. Найдем оценку среднего арифметического значения результата измерения  1 и 2 серий

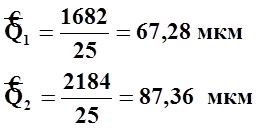
5. Найдем стандартное отклонение результата измерений 1 и 2 серий:

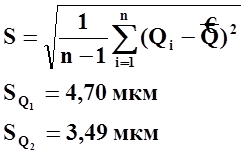
Сравним стандартные отклонения результатов измерений с двумя другими сериями, выполняемых второй подгруппой.

Видно, что массив:

Qi

61

62

63

64

66

67

68

69

70

71

72

m

1

1

2

3

3

4

2

3

2

2

2

 и  которого, незначимо отличается от нашей первой серии.

В дальнейшем будем рассматривать две серии близких по показателям (1 серия – нашей подгруппы, 2 серия, близкая по значениям – второй подгруппы)

6. Проверка нормальности результата измерения в 1 и 2 сериях по составному критерию.

Рассчитаем:

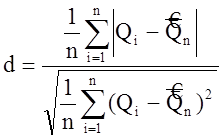
Для I серии:

Для II серии:

Проверим выполняется ли условие:  с вероятностью P*=0.99

Оба значения d1 и d2 попадают в интервал. Т.к. условие выполняется, то дополнительно проверяем «хвосты» законов распределения вероятностей, по которому считается допустимым отклонение одного из независимых значений результатов измерения Qi от среднего арифметического больше, чем на 2.5SQ.

С доверительной вероятностью P**=0.98 данное условие выполняется. Значит гипотеза о нормальности результата измерения принимается с вероятностью .

7. Проверка значимости различия между средними арифметическими в 2-х сериях:

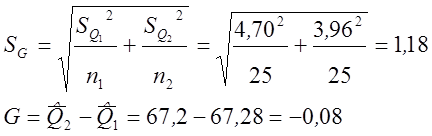
Зададимся доверительной вероятностью P=0.99 и t=2,8.

Проверим выполняется ли условие:

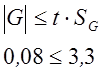
Условие выполняется, следовательно различие между средними арифметическими в сериях считается незначимым.

8. Проверка равнорассеянности результатов измерений в 2-х сериях:

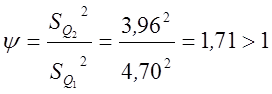
Выберем доверительную вероятность P=0.99 и определим по таблице аргумент  интегральной функции распределения вероятности Р.А.Фишера

Т.к. , то можно считать, что серии равнорассеянны

9. Дальнейшую обработку равнорассеянных серий с незначимым различием между средними арифметическими осуществляем как обработку единого массива:

№ п/п

Qi

mi

miQi

(Qi-Q)

(Qi-Q)2

mi(Qi-Q)2

1

60

2

120

-5,24

27,46

54,92

2

61

1

61

-4,24

17,98

17,98

3

62

3

186

-3,24

10,50

31,49

4

63

4

252

-2,24

5,02

20,07

5

64

6

384

-1,24

1,54

9,23

6

65

2

130

-0,24

0,06

0,12

7

66

5

330

0,76

0,58

2,89

8

67

7

469

1,76

3,10

21,68

9

68

5

340

2,76

7,62

38,09

10

69

3

207

3,76

14,14

42,41

11

70

4

280

4,76

22,66

90,63

12

71

2

142

5,76

33,18

66,36

13

72

4

288

6,76

45,70

182,79

14

73

1

73

7,76

60,22

60,22

∑

50

3262

638,86

Найдем оценку среднего квадратического отклонения результата измерения.


,

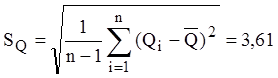
Ни одно из значений результата измерений не отличается от среднего арифметического более чем, на 3SQ=10,83 с вероятностью 0,997. Можно предположить, что ошибок нет.

Построим гистограмму.

№ п/п

границы интервала

mi

1

60-62

3

0,03

2

62-64

7

0,07

3

64-66

8

0,08

4

66-68

12

0,12

5

68-70

8

0,08

6

70-72

6

0,06


7

72-74

5

0,05

По виду гистограммы можно предположить, что результат измерения подчиняется нормальному закону распределения.

Проверим гипотезу о подчинении нормальному закону распределения по критерию К.Пирсона.

№ п/п

Границы интервала

mi

ti

L(ti)

Pi

nPi

mi-nPi

1

-∞;62

3

-0,89

-0,3133

0,1867

3,34

-0,34

0,01

2

62;64

7

-0,34

-0,1331

0,1802

4,01

2,99

0,99

3

64;66

8

0,20

0,0793

0,2124

7,62

0,38

0,01

4

66;68

12

0,76

0,2764

0,1971

11,85

0,15

0,00

5

68;70

8

1,31

0,4049

0,1285

7,25

0,75

0,09

6

70;72

6

1,86

0,4686

0,0637

5,15

0,85

0,23

7

72;∞

5

∞

0,5

0,0314

4,57

0,43

0,12

∑

1

С выбранной вероятностью 0,95 по графику интегральной функции распределения вероятностей К.Пирсона находим .

Т.к. , то гипотеза о подчинении нормальному закону распределения вероятности принимается.

мкм

D=(14997,70…15012,30) мкм

             Выводы:

1.  При многократном измерении наряду с априорной эффективно используется апостериорная информация.

2.  Многократное измерение обязательно предполагает статистическую обработку экспериментальных данных. Поэтому при оценке неопределенности результата многократного измерения всегда используется способ А.

3.  Неопределенность результата многократного измерения, обусловленная статистическим рассеянием экспериментальных данных, может быть уменьшена посредством увеличения их объема.

Скачать файл