|
Решетникова |
Рагозин |
|||||||||
|
Рабочий предел |
I1 |
I2 |
Рабочий предел |
I1 |
I2 |
|||||
|
дел |
А |
дел |
А |
дел |
А |
дел |
А |
|||
|
0¸2,5 |
23 |
0,23 |
47,2 |
1,18 |
0¸2,5 |
25 |
0,25 |
52,5 |
1,312 |
|
|
25 |
0,25 |
51,5 |
1,29 |
30 |
0,3 |
61,8 |
1,545 |
|||
|
30 |
0,3 |
62,3 |
1,56 |
32 |
0,32 |
65,8 |
1,645 |
|||
|
0¸5,0 |
34 |
0,34 |
34,8 |
1,74 |
0¸5,0 |
35 |
0,35 |
35,05 |
1,752 |
|
|
40 |
0,4 |
41,2 |
2,06 |
40 |
0,4 |
40,06 |
2,003 |
|||
|
50 |
0,5 |
50,4 |
2,52 |
45 |
0,45 |
45,08 |
2,254 |
|||
|
56 |
0,56 |
56,4 |
2,82 |
50 |
0,5 |
50,05 |
2,502 |
|||
|
61 |
0,61 |
61,5 |
3,07 |
55 |
0,55 |
55,04 |
2,752 |
|||
|
70 |
0,7 |
70,4 |
3,52 |
60 |
0,6 |
60,08 |
3,004 |
|||
|
S |
3,89 |
19,76 |
S |
3,72 |
18,769 |
|||||
|
№ эксп. |
|
I2 |
I12 |
I2I1 |
a1 |
a0 |
Функция преобразования трансформатора, I2 |
|
1 |
0,41 |
2,05 |
0,18 |
0,91 |
5,8 |
0,35 |
0,35 + 5,8 I1 |
|
2 |
0,47 |
2,38 |
0,257 |
1,302 |
5,03 |
0,03 |
0,03 + 5,03 I1 |
|
3 |
0,48 |
2,45 |
0,28 |
1,45 |
5,07 |
0,019 |
0,019 +5,07 I1 |
|
4 |
0,57 |
2,892 |
0,41 |
2,057 |
4,8 |
0,15 |
0,015 + 4,8 I1 |
|
5 |
0,41 |
2.085 |
0,0337 |
0,9237 |
4,52 |
0,85 |
0,085 + 4,52 I1 |
|
6 |
0,43 |
2,195 |
0,212 |
1,07 |
4,7 |
0,185 |
0,185 + 4,7 I1 |
Порядок обработки результатов измерений
На основании априорной информации известно, что функция преобразования трансформатора тока описывается линейным уравнением
![]()
Коэффициенты
![]() и
и ![]() ,
рассчитанные по методу наименьших квадратов:
,
рассчитанные по методу наименьших квадратов:
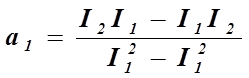
![]()
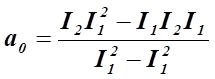
Градуировочная характеристика трансформатора тока построена на рис. 2
Выводы:
1. Для определения функции
преобразования трансформатора необходим достаточный объем априорной информации.![]()
2. Применение метода наименьших квадратов позволяет построить градуировочную характеристику, удовлетворяющую требованиям минимизации квадратов отклонений от ее экспериментальных точек.
3. Линейная градуировочная
характеристика определяет коэффициент преобразования трансформатора: ![]()
ЛАБОРАТОРНАЯ РАБОТА № 4
Многократное измерение диаметра калибра гладкого
Состав оборудования:
Задание на лабораторную работу
Выполнить многократное измерение диаметр калибра гладкого.
Теоретические выкладки
1. Предел измерения оптиметра 100мкм, а диаметр калибра гладкого больше 1 см. Поэтому точное измерение оптиметром диаметра калибра гладкого возможно только при использовании дополнительного набора концевых мер длины. В этом случае результат измерения диаметра D калибра гладкого будет
D=LS+Lopt, (1)
где LS -суммарная длина концевых мер длины;
Lopt –среднее арифметическое значение показания оптиметра.
2. Неопределенность LS будет складываться из неопределенности значений концевых мер длины:
![]() , (2)
, (2)
меры при которых ui находятся методом ситуационного моделирования (способом В).
3. Неопределенность Lopt при многократном измерении диаметра гладкого находится посредством статической обработки экспериментальных данных (способом А).
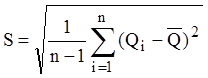 , (3)
, (3)
4. Неопределенность калибра гладкого D характеризуется величиной
![]() . (4)
. (4)
5. Измеренное значение диаметра калибра гладкого находится в пределах
от D-2u до D+2u.
Необходимая априорная информация
1. Оптиметр вертикальный ОВ-1:
– диапазон (0÷100 мкм);
– цена деления – 1 мкм;
2. Концевые меры:
– класс точности 2;
Порядок выполнения работы
1. Изучить устройство оптиметра и методику выполнения измерений.
2. Составить необходимый набор концевых мер длины. Определить номинальное значение длины набора Lå и меру неопределенности этого значения uå .
3. Выполнить две серии многократных измерений диаметра калибра гладкого.
4. Проверить, нет ли ошибок в массиве экспериментальных данных. В случае их обнаружения ошибочные значения отбросить.
5. Проверить, подчиняется или нет показание оптиметра нормальному закону распределения вероятности.
6. Найти меру неопределенности показания оптиметра использовать формулу (3).
7. Найти меру неопределенности результата измерения диаметра калибра гладкого по формуле (4).
8. Установить интервал, в пределах которого находится значение диаметра калибра гладкого.
Получение и обработка экспериментальных данных
1. Номинальное значение длины набора концевых мер LS1=15,5 мм, LS2=15,05 мм
2. Мера
неопределенности для первой серии:![]() ,
,
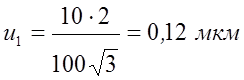
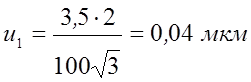
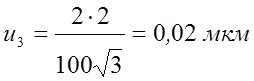
![]()
Мера неопределенности для второй
серии: ![]() ,
,
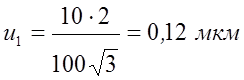
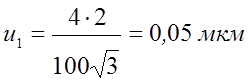
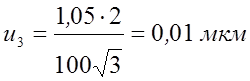
3. Массив экспериментальных данных (мкм):
1 серия
|
Qi |
60 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
70 |
72 |
73 |
|
m |
2 |
3 |
2 |
3 |
2 |
2 |
3 |
3 |
2 |
2 |
1 |
2 серия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.