Определение коэффициента теплоотдачи при свободном конвективном теплообмене поперечно обтекаемого круглого цилиндра

Передача теплоты конвекцией всегда связана с теплопроводностью в пограничном слое.

Из гидравлики известно, что движение может быть ламинарным, переходным n турбулентным, что определяется величиной числа подобия Рейнольдса

R_e=, где w - скорость потока, м/с;

l - геометрический характерный размер, м ;

v - кинематическая вязкость жидкости, м/с,

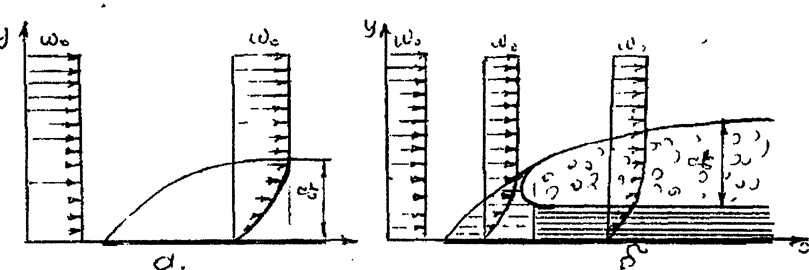
Рис. 1. Гидродинамический пограничный слой

Тонкий слой жидкости вблизи поверхности тела, в котором происходит изменение скорости жидкости от нуля непосредственно на стенке до скорости невозмущенного наличием стенки потока w₀ называют гидродинамическим пограничным слоем. Толщина его d_г возрастает вдоль по потоку. Этот слой может быть ламинарным или турбулентным с ламинарным подслоем в зависимости от скорости невозмущенного потока.

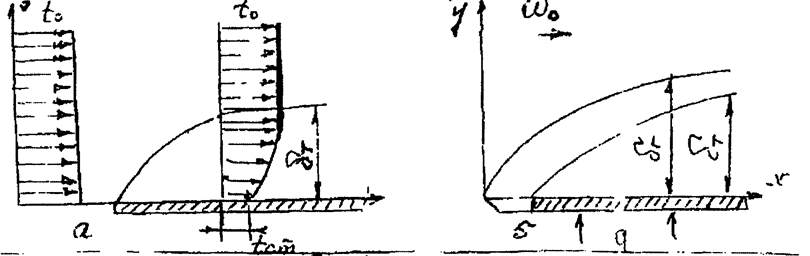
Рис. 2. Тепловой пограничный слой.

Если температура стенки и жидкости неодинаковы, то вблизи стенки образуется тепловой пограничный слой, в котором происходит изменение температуры жидкости от температуры стенки до температуры ядра потока t₀. Толщины гидродинамического и тепловых слоев могут не совпадать.

Дифференциальное уравнение,  описывающее  процесс  конвективного теплообмена на поверхности тела, омываемого потоком теплоносителя, имеет следующий вид:

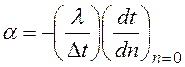,                                         (1)

где a – коэффициент теплоотдачи от стенки теплоносителю или от теплоносителя стенке, Вт/м²град

l – коэффициент теплопроводности жидкости, Вт/м.град

t – температура, град;

n – нормаль, м.

Если рассмотреть два подобных явления конвективного теплообмена, то константы подобия (это отношение параметров первой системы – натуры к параметрам второй системы – модели в сходственных точках в сходственные моменты времени) будут следующими:

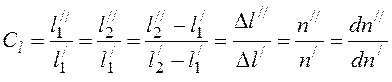 - константа геометрического подобия (вспомните из школьной геометрии - подобные фигуры, их свойства);

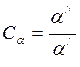 - константы подобия процессов конвективного теплообмена в двух подобных системах;

C_t=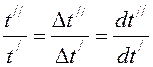 - константы подобия температурного поля.

Для двух подобных систем конвективного теплообмена можно записать уравнение (1)

для первой системы – 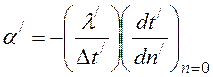                                                         (2)

для второй системы 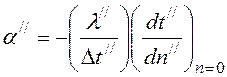                                                           (3)

Подставив в уравнение (3) параметры второй системы (" - два штриха), полученные из констант подобия (например,a^//=C_a×a^/и т.д.), получим:

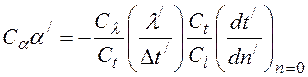
или

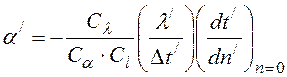                                                           (4)

Уравнение (2) и (4) тождественны, так как они описывают связь между параметрами конвективного теплообмена двух подобных систем, описанную дифференциальным уравнением конвективного теплообмена для двух сходственных точек. Из условия тождественности следует, что величина, называемая константой подобия, равна 1:

C=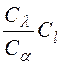=1                                                          (5)

Подставив значение констант (например, С_a=a^///a^/ — и т.д.), получим уравнение (5) в другом виде:

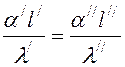                                                       (6)

Таким образом, мы получили объединение - комплекс параметров, описывающих конвективный теплообмен, что дает возможности сократить число переменных, который называют числом подобия (в старых учебниках критерием подобия). Числа подобия принято называть именами крупных ученых, известных своими работами в области теплообмена и гидродинамики (см. табл.1). Число подобия (6) называют числом Нуссельта и обозначают первыми буквами фамилии (как и число Re - число гидродинамического подобия):

N_u=                                                            (7)

При помощи теории подобия удается, не интегрируя сложные дифференциальные уравнения теории пограничного слоя (см./1/, стр. 362), получить их решения в числах подобия:

N_u=f(Re,Gr,Pr)                                                     (8)

Таблица 1. Числа подобия

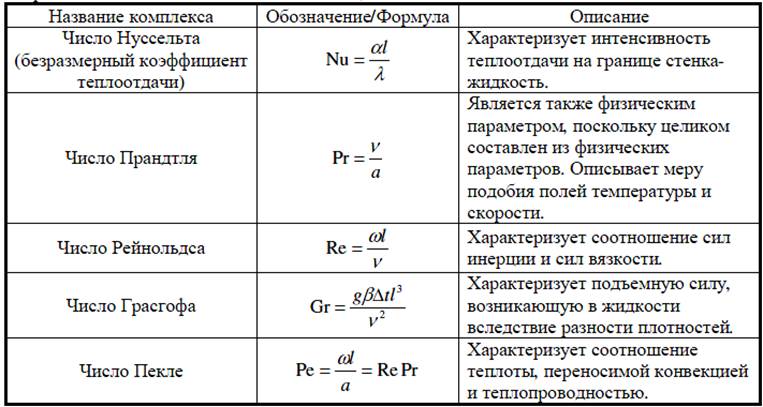
После изучения на моделях конвективного теплообмена был найден общий вид решения уравнения, в котором коэффициенты определяются для конкретных случаев по экспериментальным данным:

N_u=cReⁿ Gr^b Pr^m (Pr_ж/Pr_ст)     (9),

где

Gr=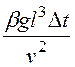—число Грасгофа,                              (10)

Рr=  — число Прандтля,

b - температурный коэффициент расширения среды, 1/град (для газов b=1/Т);

g - ускорение свободного падения;

Dt - перегрев жидкости на стенке (разница температуры стенки и воздуха)

а - коэффициент температуропроводности.

В каждом случае использования полуэмпирических уравнений необходимо разобраться, что автор уравнения принимал за характерный размер и определяющую температуру, по которой из справочной литературы находят значения теплофизических  свойств теплоносителя.

Описание лабораторной установки

Лабораторная установка (см. рис.3) представляет собой металлическую трубу Т длиной L и диаметром d, внутри которой расположен ТЭН (теплонагревательный элемент - нихромовая спираль). На ТЭН через ЛАТР (лабораторный автотрансформатор) подается напряжение переменного тока. Электрические измерительные приборы позволяют зарегистрировать величины силы тока I и падения напряжения U во время эксперимента.

Температура поверхности стенки tст измеряется термопарами 1…5, закрепленными в нескольких точках по длине трубы, показания термопар отображаются цифровым термометром ЦТ. Для переключения термопар цифровой термометр оснащен многопозиционным переключателем П.

Температура окружающего воздуха tо измеряется жидкостным термометром, размещенным на удалении от установки.

Геометрические размеры трубы измеряются: длина L -  линейкой, диаметр d – штангенциркулем.

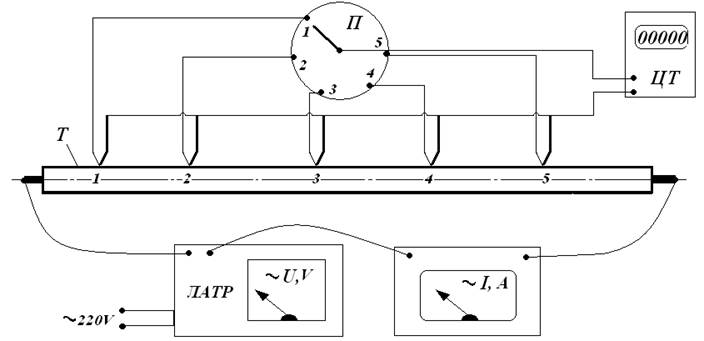
Рис.3. Схема экспериментальной установки

Экспериментальное определение коэффициента теплоотдачи

1. Выполняют измерения в соответствии с содержанием таблицы измерений:

U, В	I, А	tст, ºC	tо, ºC	d, м	L, м
		1) 2) 3) 4) 5)

2. По величинам силы тока I и падения напряжения U и определяют