Введение в метрологическое обеспечение в строительстве. Предмет и задачи метрологии. Физические величины, их единицы и системы единиц

одинаковой точностью и величины ошибок измерения соответствуют нормальному закону распределения, то параметры исследуемого уравнения определяются из условия, при котором сумма квадратов отклонений измеренных значений от расчетных принимает наименьшее значение. При этом нахождение неизвестных параметров (а₁, а₂, ..., а_n) сводится к решению системы линейных алгебраических уравнений:

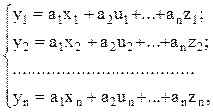                       (3.43)

где y₁, y₂, ..., y_n - частные значения измеренных величин искомой функции y; x, u, z - переменные величины. Эту систему приводят к системе линейных уравнений путем умножения каждого уравнения соответственно на х₁, х₂, ..., х_n, последующего их сложения и умножения соответственно на u₁, u₂, ..., u_n. При этом получается система так называемых нормальных уравнений:

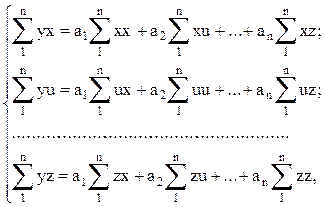          (3.44)

решение которой и дает искомые коэффициенты.

Регрессионный анализ

Очень часто между переменными х и y существует связь, при которой одному значению аргумента соответствует некоторая совокупность значений функции (статистический ряд распределения y). Такую связь называют корреляционной (регрессионной). Следовательно, регрессионные зависимости характеризуются вероятностными и стохастическими связями. Поэтому для установления таких зависимостей необходимо наличие статистических измерений.

Сущность регрессионного анализа заключается в определении уравнения регрессии, устанавливающего связь между случайными величинами (аргументами х_i и функцией y), оценке тесноты связи между ними, достоверности и адекватности результатов измерений.

Для предварительного установления наличия такой связи между х и у результаты измерений представляются графически, то есть строится корреляционное поле (рис. 3.9). По тесноте группирования точек вокруг прямой или кривой линий можно визуально судить о наличии или отсутствии корреляционной связи. Так, на рисунке 3.9-а видно, что между х и у существует определенная связь, в то время как из рисунка 2.9-б следует, что изображенный на нем процесс такой связи не показывает.

Даже для вполне выраженной формы корреляционного поля вследствие статистического характера связи одному значению х соответствует некоторое множество значений у. Если на корреляционном поле осреднить точки, то есть для дискретных значений х_i подсчитать осредненное значение  и соединить их, то получим ломаную линию, которая носит название экспериментальной регрессионной зависимости (линии). Если на корреляционном поле провести плавную кривую, равноудаленную от значений , то получится теоретическая регрессионная зависимость (линия АБ на рисунке 3.9-а).

Различают однофакторные (парные) и многофакторные регрессионные зависимости. Парная регрессия может быть аппроксимирована какой-либо элементарной функцией: прямой линией, параболой, гиперболой и т. п. Двухфакторное корреляционное поле можно аппроксимировать, например, плоскостью, параболоидом второго порядка, гиперболоидом.

При построении теоретической регрессионной зависимости оптимальной является такая функция, у которой соблюдается условие наименьшего квадратичного отклонения:

Если регрессионная зависимость описывается прямой линией у = а + bx, то коэффициенты уравнения вычисляются из следующих соотношений:

       (3.45)

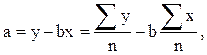                      (3.46)

где n - число измерений.

Критерием близости корреляционной зависимости между х и у к линейной функциональной зависимости является коэффициент парной корреляции или просто коэффициент корреляции r, который показывает степень тесноты связи между х и у. Этот коэффициент подсчитывается из выражения

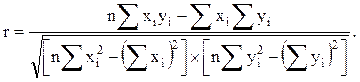      (3.47)

При r = 1 между х и у существует функциональная зависимость, то есть