Конструктивные схемы сборных балочных перекрытий. Расчётная схема и расчётный пролёт. Постоянная нагрузка, действующая на плиту

умножения соответствующих нагрузок на 1м² перекрытия на ширину плиты  b_pan=1,4 м и   коэффициент надёжности по назначению здания   .

Расчётная полная нагрузка на 1 м длины плиты:

 .

Нормативная полная нагрузка на 1 м длины плиты:

 , в том числе нормативная постоянная и длительная нагрузка :

 .

Таблица 1.1

Нормативные и расчётные нагрузки на  1м² перекрытия

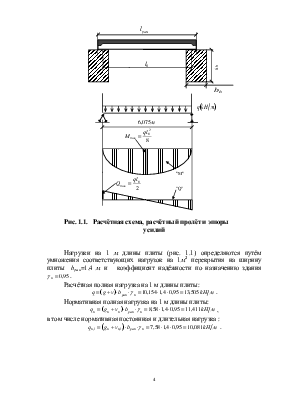
1.3.   Усилия от расчётных и нормативных нагрузок

Расчётная схема панели показана на рис. 1.1 . Для такой балки наибольший изгибающий момент в середине пролёта равен  , а наибольшая поперечная сила на опоре равна  . Тогда усилия :

-  от расчётной полной нагрузки

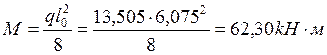;                                  (1.2)

;

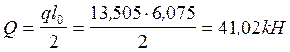-  от нормативной полной нагрузки

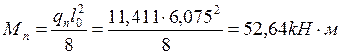;                                                (1.3)

;

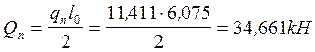-  от нормативной постоянной и длительной нагрузки

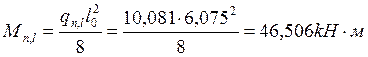       .                               (1.4)

1.4.   Компоновка поперечного сечения плиты

Принимается панель со следующими параметрами (рис. 1.2 а):

ширина панели по низу   140 - 1=139 см;

ширина панели по верху  140 - 2 ^. 2=136 см;

толщина полки  -   5 см;

ширина продольных рёбер по низу  -   7 см;

высота поперечного сечения ребристой предварительно напряженной плиты :

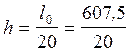 , принимаем h = 30 см;

толщина защитного слоя бетона для рабочей арматуры рёбер  -   а = 3 см; рабочая высота сечения  h₀ = h - a = 27 см .

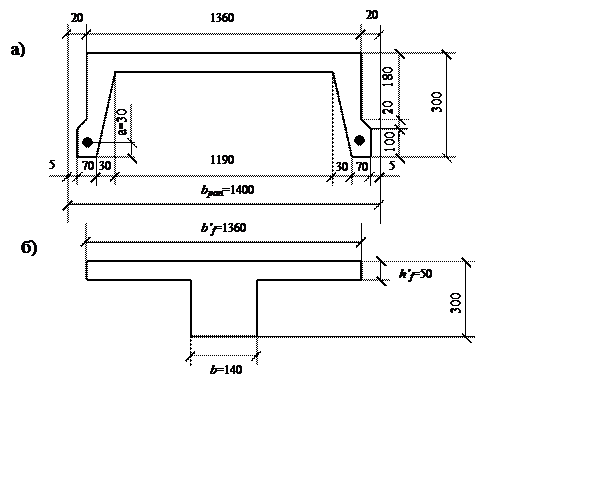а - поперечное сечение; б - приведённое сечение

При расчёте по предельным состояниям П-образное поперечное сечение ребристой плиты приводится к эквивалентному тавровому сечению (рисунок 1.2 б) с шириной полки b'_f = 136 см, толщиной    полки      h'_f = 5 см, высотой  h = 30 см и шириной      ребра   b = 2 ^. 7= 14 см. Так как    h'_f /h=5/30 > 0,1 , то согласно /1, п. 3.16 / в расчёт вводится вся ширина полки  b'_f = 136 см .

1. 5.   Материалы для панели

Ребристая панель перекрытия проектируется предварительно напряжённой с электротермическим натяжением арматуры на упоры форм. Изделие подвергается тепловой обработке при атмосферном давлении.

Рабочую предварительно напряжённую арматуру продольных рёбер принимаем класса А-V:

нормативное сопротивление R_sn = 785 МПа;

расчётное сопротивление      R_s = 680 МПа;

модуль упругости                   E_s = 1,9 ^. 10⁵ МПа.

Характеристики арматуры A-V приняты по приложению 4. В качестве ненапрягаемой арматуры плиты будем использовать стержневую арматуру класса A-III и обыкновенную арматурную проволоку периодического профиля класса B_p-I.

Для изготовления плиты выбираем бетон класса В30 с характеристиками согласно приложений 1, 2 и 3:

нормативная призменная прочность, МПа                  R_bn =R_b,ser= 22;

расчётная призменная прочность , МПа                                 R_b= 17 ;

нормативное сопротивление при растяжении, МПа R_btn=R_bt,ser=1,8 ;

расчётное сопротивление при растяжении, МПа                 R_bt= 1,2 ;

коэффициент условий работы бетона                                    g_b2 = 0,9;

начальный модуль упругости бетона, МПа                     E_b= 2,9 ^. 10⁴.

Предварительное напряжение в напрягаемой арматуре в соответствии с /1, п. 1.23/ должно удовлетворять условиям:

        и        .

При электротермическом натяжении арматуры на упоры форм допустимое отклонение значения предварительного напряжения равно:

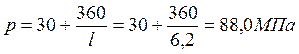, где  l -  длина натягиваемого стержня (расстояние между наружными гранями упоров), м .

Тогда .Принимаем . При этом неравенство  690 - 88 > 0,3 ^. 785  выполняется.  Значение предварительного напряжения в арматуре   вводится в расчёт с коэффициентом точности натяжения  согласно /1, п. 1.27/, определяемым по формуле (при электротермическом способе натяжения):

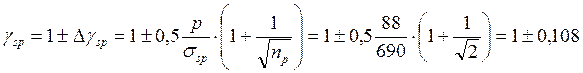 ,       (1.5)

где  n_p -  число стержней напрягаемой арматуры.

Параметр   принимается по расчёту, но не менее 0,1.

При определении потерь предварительного напряжения арматуры, а также при расчёте по раскрытию трещин и по деформациям   допускается принимать равным 1.

В соответствии с /1, п. 3.12/ вычислим граничную относительную высоту сжатой зоны по формуле:

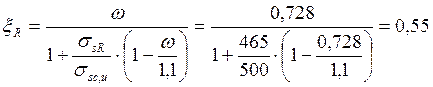,                        (1.6)

где   -  характеристика сжатой зоны бетона, равная

0,85 - 0,008R_b= 0,85 - 0,008 ^. 0,9 ^. 17= 0,728 ;

 -  напряжение в арматуре, МПа, принимаемое равным

 (здесь  принимается при коэффициенте   и   при электротермическом натяжении);

 -  предельное напряжение в арматуре сжатой зоны, принимаемое равным  500 МПа так как  .

1.6. Расчёт ребристой плиты по предельным состояниям первой

       группы

1.6.1. Расчёт прочности плиты по сечению, нормальному

          к продольной оси

Расчёт прочности плиты выполняем как балки таврового сечения (рис. 1.2 б) при максимальном изгибающем моменте в середине пролёта     М = 62,3 kH^.м .

Проектирование такого изгибаемого элемента следует осуществлять так, чтобы арматура в растянутой зоне работала с расчетным сопротивлением R_S , то есть с напряжением, равным пределу текучести (физическому или условному). Поэтому усилие в арматуре в стадии предельного равновесия будет равно N_S=R_S · A_SP. В то же время усилие в сжатом бетоне N_Ь составит R_Ь · A_Ь, так как считается, что все волокна сжатой зоны бетона высотой x имеют одинаковое значение напряжения равное R_Ь (рис. 1.3).

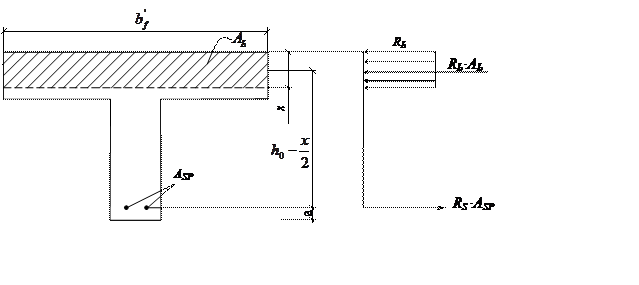Рис. 1.3. К расчету прочности нормальных сечений изгибаемых элементов

Исходя из вышеизложенного можно записать уравнение равновесия в нормальном сечении элемента, полагая что в предельной стадии момент от внешней нагрузки М не превышает (равен) внутреннего момента, создаваемого сжатым бетоном и растянутой арматурой, то есть 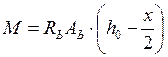 или 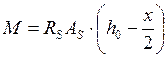. Для вычисления требуемой площади арматуры перепишем эти выражения, полагая  согласно